[BOJ 2667] 단지번호붙이기

풀이

문제를 보자마자 BFS 방식으로 접근하였다. 하나씩 깊게 탐색하는 DFS에 비해 여러 개씩 넓게 탐색하는 BFS가 효율적이라고 생각했기 때문이다. 전체적인 로직은 아래와 같다.

1. (0,0)부터 상하좌우에 연결된 집이 있는지 확인한다.

2. 연결된 집이 있으면 단지화 시킨다.

3. 모든 집에 대해서 위 과정을 수행한다.

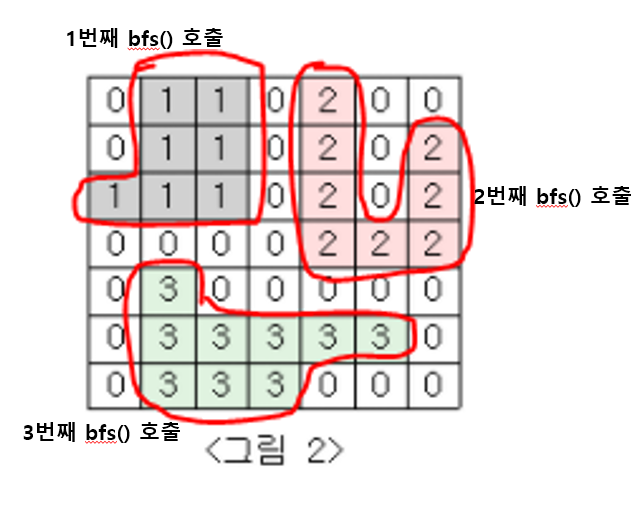
문제에서 주어진 테스트 케이스를 통해 저의 코드를 간략하게 설명하겠다. 문제에서 주어진 테스트 케이스를 입력하게 되면 총 3번의 bfs() 함수를 호출하게 된다. for문 안의 조건으로 총 단지 수를 구해주고, bfs() 함수에서 각 단지에 속해있는 집의 수를 구하게 된다.

코드

# BFS
import sys
from collections import deque

input = sys.stdin.readline
N = int(input())
plan = [list(map(int, input().rstrip())) for _ in range(N)]

visited = [[False] * N for _ in range(N)]
dir = [[-1, 0], [1, 0], [0, -1], [0, 1]]
q = deque([])
total = 0
house_complex = []


# 1인 것부터 탐색하기 때문에 home = 1로 초기화
# bfs() 호출할 시 1개의 단지 안에 속하는 집의 수를 구해주게 된다.
def bfs():
    home = 1
    while q:
        r, c = q.popleft()
        for i in range(4):
            nr = r + dir[i][0]
            nc = c + dir[i][1]
            if 0 <= nr < N and 0 <= nc < N and not visited[nr][nc] and plan[nr][nc] == 1:
                visited[nr][nc] = True
                q.append((nr, nc))
                home += 1
    house_complex.append(home)


for i in range(N):
    for j in range(N):
        # 백준 예제에서는 총 3번 BFS() 함수 호출된다고 생각하면 쉽다. (전체 단지 덩어리 수)
        if not visited[i][j] and plan[i][j] == 1:
            q.append((i, j))
            visited[i][j] = True
            total += 1
            bfs()

house_complex.sort()
# print(len(house_complex))
print(total)

for hc in house_complex:
    print(hc)