Union-Find란?

• Disjoint-Set을 구현할 때 사용하는 알고리즘.

  • 집합을 구현하는데 비트 벡터, 배열, 연결리스트를 사용할 수 있으나, 가장 효율적인 트리 구조를 이용하여 구현함.

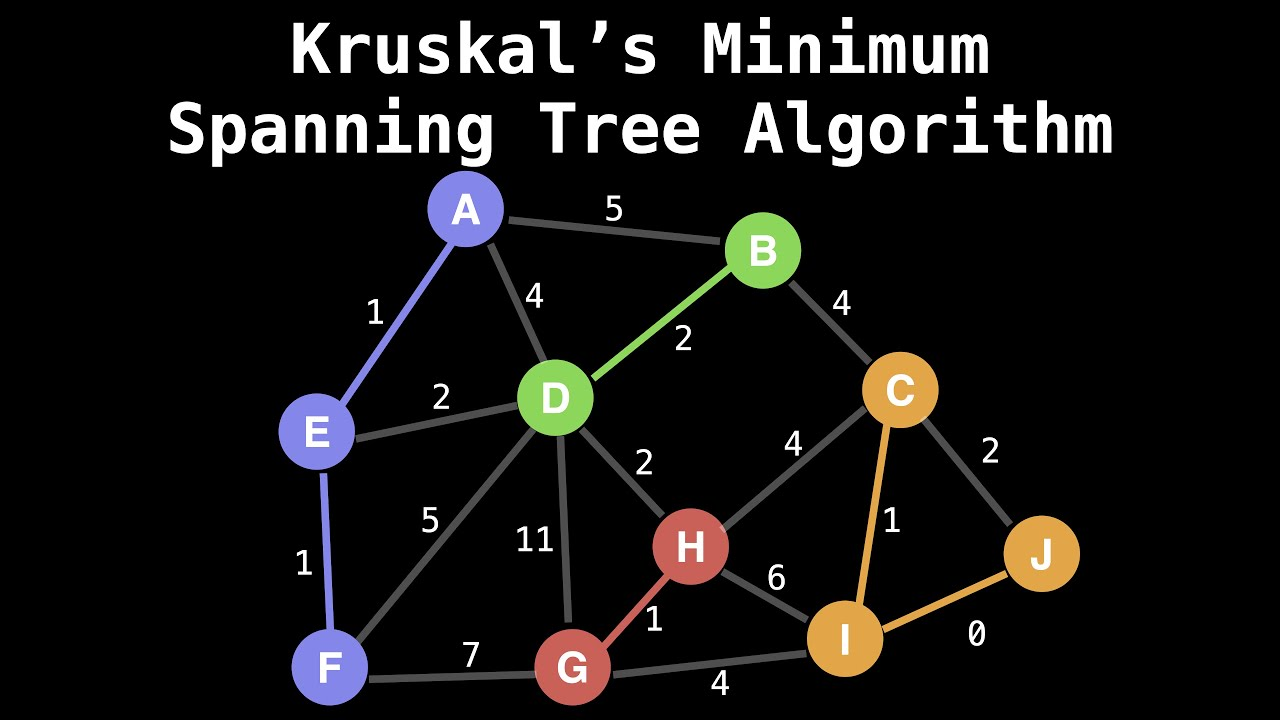
• 크루스칼 알고리즘에서 그래프의 최소 신장 트리(MST)를 찾는데 활용된다. (정점 연결 및 사이클 형성 여부 확인)

• 초기에 {0}, {1}, {2}, … {n} 이 각각 n+1개의 집합을 이루고 있다. 여기에 합집합 연산과, 두 원소가 같은 집합에 포함되어 있는지를 확인하는 연산을 수행하려는 경우. 집합의 표현-백준1717번

• 어떤 사이트의 친구 관계가 생긴 순서대로 주어졌을 때, 가입한 두 사람의 친구 네트워크에 몇 명이 있는지 구하는 프로그램을 작성하는 경우. 친구 네트워크-백준4195번

그러면 Disjoint-Set은 뭔데?

서로소 집합 자료구조라고 부른다.

• 서로 중복되지 않는 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조
  • 즉, 공통 원소가 없는 상호 배타적인 부분 집합들로 나눠진 원소들에 대한 자료구조이다.

• 상호 배타적을 확실히 이해해야한다. --> A, B 사건이 존재한다면, A, B는 동시에 일어나지 않고 둘 중 하나만 일어나야 한다. (P(A) + P(B))
  <-> ※독립은 사건 A, B가 동시에 일어나도 상관없음.

Union-Find 기능과 구현

먼저 union() 함수와 find() 함수의 기능을 간단히 정리한 후 Python 코드를 살펴보겠다.

• union(parent, x, y)
  • 합하기, 연결하기
  • x가 속한 집합과 y가 속한 집합을 합친다. 즉, x와 y가 속한 두 집합을 합치는 연산.

• find(parent, x)
  • 찾기 (속한 그룹 찾기 = 부모 찾기)
  • x가 속한 집합의 대표값(루트 노드 값)을 반환한다. 즉, x가 어떤 집합에 속해 있는지 찾는 연산.

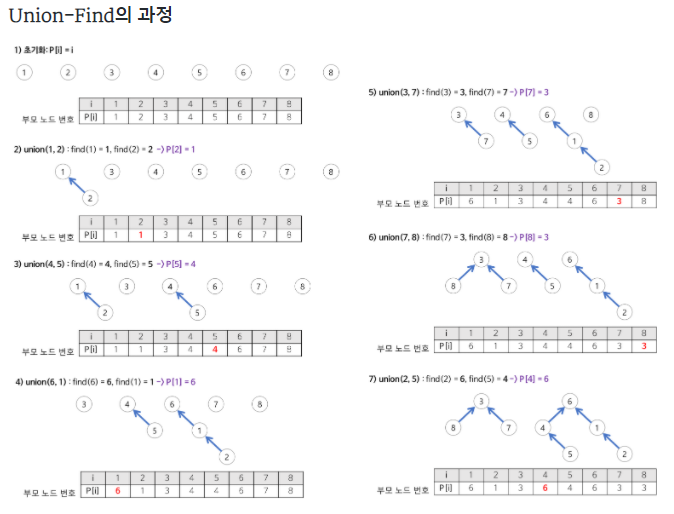
사진 출처 : 링크

기본적인 구현 방법

parents = [i for i in range(MAX_SIZE)]


# 재귀 함수
def find(parent, x):
    # 루트 노드의 부모 노드 번호는 자기 자신이다.
    if parent[x] == x:
        return x

    # 각 노드의 부모 노드를 찾아 올라간다.
    else:
        return find(parent, parent[x])


def union(parent, x, y):
    # 각 원소가 속한 트리의 루트 노드를 찾는다.
    rootX = find(parent, x)
    rootY = find(parent, y)

    parent[rootY] = rootX

위 코드는 기본적인 union-find 구현 방법이다. 하지만, 트리의 모든 높이를 탐색해야하는 최악의 경우에는 비효율적인 성능을 보여준다.

• 트리 구조가 완전 비대칭인 경우
• 연결리스트 형태
• 트리의 높이가 최대가 된다.
• 원소의 개수가 N일 때, 트리의 높이는 N-1이므로 union()과 find() 함수의 시간복잡도는 모두 O(N)이 된다.
• 배열로 구현하는 것보다 비효율적이다.

따라서 우리는 좀 더 효율적인 union-find 알고리즘을 구현해야 한다. 그 코드는 아래에서 설명하겠다.

---

최적화된 union-find 알고리즘

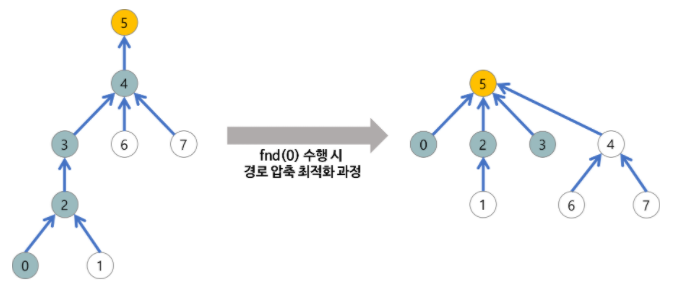
find 최적화 (=경로 압축)

parents = [i for i in range(MAX_SIZE)]


def find(parent, x):
    if parent[x] == x:
        return x

    # 경로 압축(Path Compression)
    # find 하면서 만나는 모든 값의 부모 노드를 root로 만듦.
    parent[x] = find(parent, parent[x])
    return parent[x]

O(logN)의 시간복잡도로 효율이 좋다.

(Ex) 아래 예제를 통해 직접 손코딩해서 이해해보자!

union 최적화 (union-by-rank(=height))

parents = [i for i in range(MAX_SIZE)]
rank = [0 for _ in range(MAX_SIZE)]


# find()는 위와 동일
def union(parent, x, y, rank):
    rootX = find(parent, x)
    rootY = find(parent, y)

    # 두 값의 root가 같으면(이미 같은 트리) 연결 X(합치지 않음)
    if rootX == rootY:
        return

    # union-by-rank 최적화
    # 항상 높이가 더 낮은 트리를 높이가 높은 트리 밑에 넣음.
    # --> 높이가 더 높은 쪽을 root로 함.
    if rank[rootX] < rank[rootY]:
        parent[rootX] = rootY
    else:
        parent[rootY] = rootX
        if rank[rootX] == rank[rootY]:
            rank[rootX] += 1    # 만약 높이가 같다면 합친 후 -> x 높이 + 1

참고 : https://ko.wikipedia.org/wiki/%EC%84%9C%EB%A1%9C%EC%86%8C_%EC%A7%91%ED%95%A9_%EC%9E%90%EB%A3%8C_%EA%B5%AC%EC%A1%B0#cite_note-4
https://mygumi.tistory.com/246
https://gmlwjd9405.github.io/2018/08/31/algorithm-union-find.html
https://www.weeklyps.com/entry/%EC%9C%A0%EB%8B%88%EC%98%A8-%ED%8C%8C%EC%9D%B8%EB%93%9C-Unionfind
https://bowbowbow.tistory.com/26