트리(Tree)란?
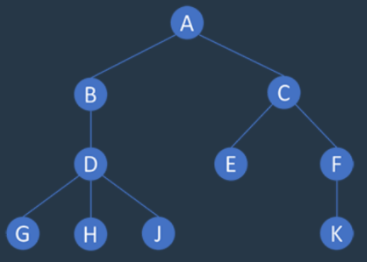
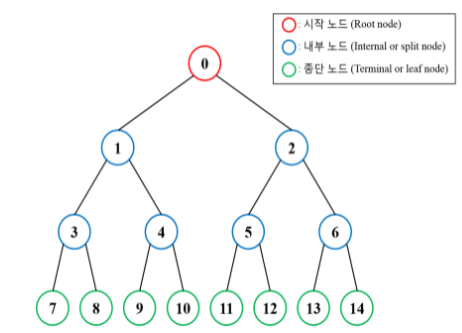
사진의 출처 : 링크
-
트리(Tree)는 그래프의 일종으로 정점과 간선을 이용하여 데이터의 배치 형태를 추상화한 자료구조이다. -
서로 다른 두 노드를 연결하는 길이 하나뿐인 그래프를
트리라고 부른다. -
힙(Heap)을 구현하는 방법 중 하나가
트리이다.
트리(Tree)의 특징
-
트리자료구조는 일반적으로 대상 정보의 각 항목들을 계층적으로 구조화할 때 사용하는 비선형 자료구조이다. -
트리의 구조는 '데이터 저장'의 의미보다는 '저장된 데이터를 더 효과적으로 탐색'하기 위해서 사용된다. -
리스트와 다르게 데이터가 단순히 나열되는 구조 X -->트리는 부모(parent)와 자식(child)의 계층적인 관계로 표현된다. -
트리는 사이클이 없다. -
트리에서 루트노드를 제외한 모든 노드는 단 하나의 부모노드를 가진다.
트리(Tree) 순회
트리의 순회란 트리의 각 노드를 체계적인 방법으로 탐색하는 과정을 의미한다. 노드를 탐색하는 순서에 따라 전위 순회, 중위 순회, 후위 순회 3가지로 분류된다.
1. 전위 순회 (Preorder)

루트노드 --> 왼쪽 서브트리 --> 오른쪽 서브트리 의 순서로 순회하는 방식이다. 깊이 우선 순회라고도 불린다.
2. 중위 순회 (Inorder)

왼쪽 서브트리 --> 노드 --> 오른쪽 서브트리 의 순서로 순회하는 방식이다. 대칭 순회라고도 불린다.
3. 후위 순회 (Postorder)

왼쪽 서브트리 --> 오른쪽 서브트리 --> 노드 의 순서로 순회하는 방식이다.
이진 트리 (Binary Tree)
-
트리자료구조는 여러 가지 유형이 있는데, 그중 가장 기본이 되는 트리는이진 트리(Binary Tree)구조이다. -
이진 트리는 2개 이하의 자식노드를 가진다. (자식노드가 없거나 1개의 자식노드만 가지는 것도 가능!) -
2개의 자식노드 중에서 왼쪽의 노드를
Left Node라고 하고, 오른쪽의 노드를Right Node라고 한다.
이진 트리의 종류
편향 이진 트리 (Skewed Binary Tree)
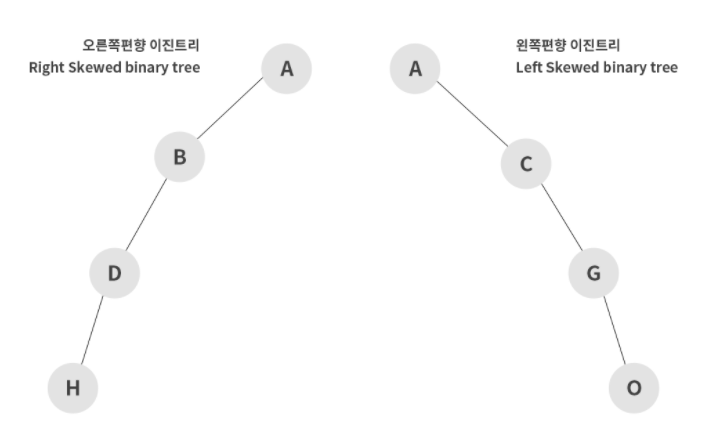
편향 이진 트리는 하나의 차수로만 이루어져 있는 경우를 의미한다. 이러한 구조는 배열(리스트)와 같은 선형 구조이므로 'Leaf Node'(가장 아래쪽에 위치한 노드) 탐색 시 모두 데이터를 전부 탐색해야 한다는 단점이 있어 효율적이지 못하다. (이를 보완하기 위해 높이 균형 트리라는 것이 있다.)
포화 이진 트리 (Full Binary Tree)
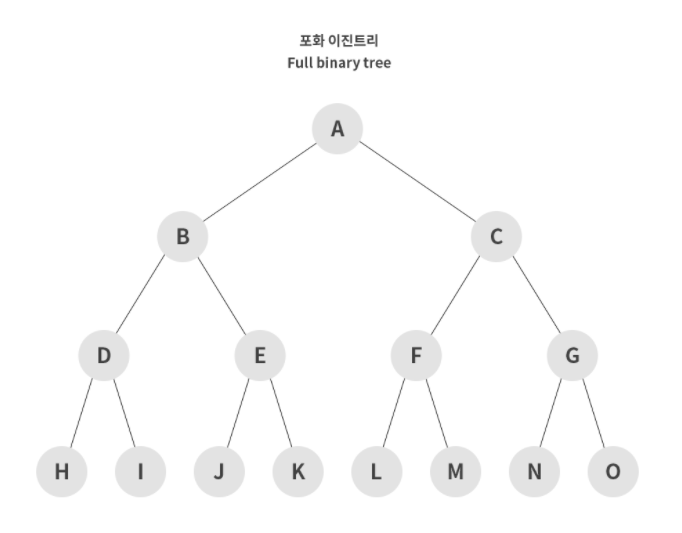
포화 이진 트리는 'Leaf Node'를 제외한 모든 노드의 차수가 2개로 이루어져 있는 경우를 의미한다. 이 경우 해당 차수에 몇 개의 노드가 존재하는지 바로 알 수 있으므로 노드의 개수를 파악할 때 용이한 장점이 있다.
완전 이진 트리 (Complete Binary Tree)
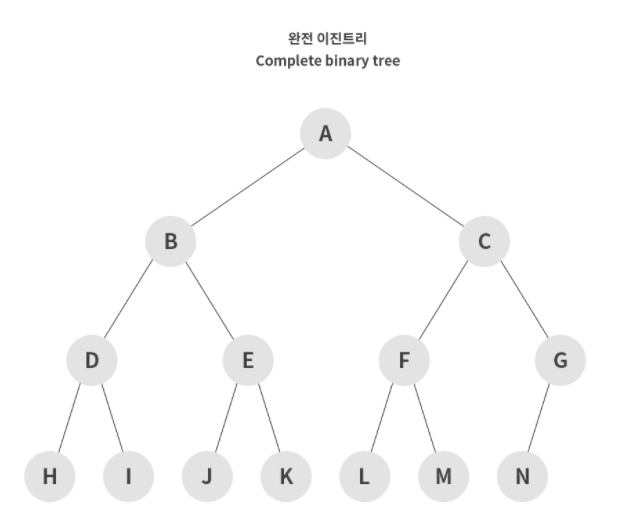
포화 이진 트리와 같은 개념으로 트리를 생성하지만, 모든 노드가 왼쪽부터 차근차근 생성되는 이진 트리를 의미한다.
※ 힙(Heap)은 완전 이진 트리의 일종이다!
이진 탐색 트리 (Binary Search Tree)
이진 탐색 트리(Binary Search Tree)는 탐색을 위한 이진 트리 기반의 자료구조이다. 아래와 같은 특징을 갖는다.
-
left node에는 부모노드보다 작은 값이 저장된다. -
right node에는 부모노드와 값이 같거나 큰 값이 저장된다. -
모든 노드는 중복된 값을 가지지 않는다.
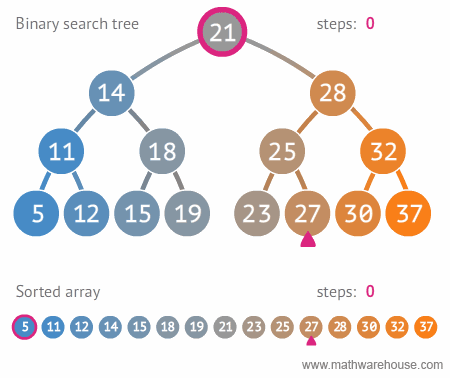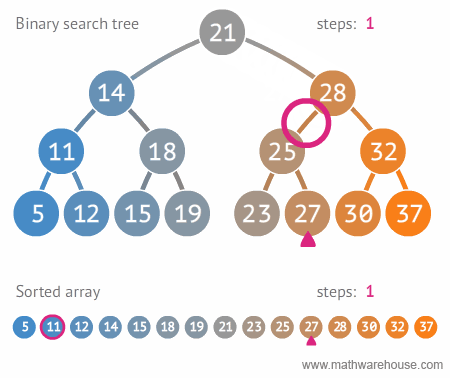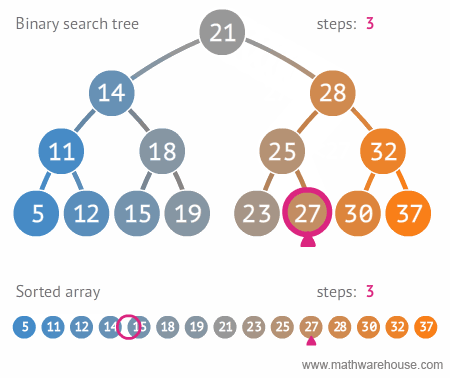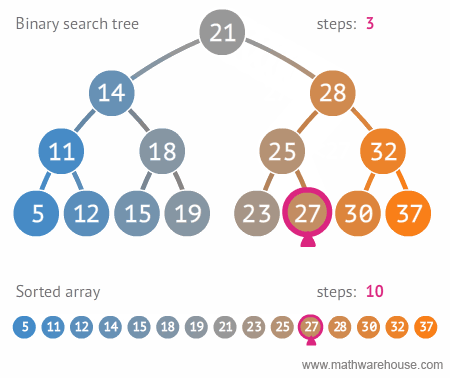
예제를 통해 이진 탐색 트리에 대해 알아보자!
(Ex) [28, 21, 15, 14, 32, 25, 18, 11, 30, 19]를
이진 탐색 트리의 형태로 만들어보자.

위와 같이 이진 탐색 트리를 만들었다. 왜 이진 탐색 트리 형태로 만들까? 바로 데이터를 효율적으로 검색(탐색)할 수 있기 때문이다!
원하는 값을 찾을 때까지 현재의 노드값보다 찾고자하는 값이 작으면 왼쪽으로 움직이고, 크면 오른쪽으로 움직인다. 이렇게 원하는 값을 더 빠르게 찾을 수 있게 된다.
이진 탐색 트리(Binary Search Tree) 구현 코드 (Python)
class Node:
def __init__(self, data):
self.left = None
self.right = None
self.data = data
# 이진 탐색 트리에 노드 삽입
def insert(self, data):
if self.data:
if data < self.data:
if self.left is None:
self.left = Node(data)
else:
self.left.insert(data)
elif data > self.data:
if self.right is None:
self.right = Node(data)
else:
self.right.insert(data)
else:
self.data = data
# 이진 탐색 트리에서 찾고자하는 값 탐색
def search(self, want_word):
if want_word < self.data:
if self.left is None:
return str(want_word) + " Not Found"
return self.left.search(want_word)
elif want_word > self.data:
if self.right is None:
return str(want_word) + " Not Found"
return self.right.search(want_word)
else:
print(str(self.data) + ' is Found')
# 이진 탐색 트리 출력
def print_Tree(self):
if self.left:
self.left.print_Tree()
print(self.data)
if self.right:
self.right.print_Tree()
root = Node(10)
root.insert(9)
root.insert(8)
root.insert(7)
print(root.search(7))
print(root.search(21))
>>> 7 is Found
>>> 21 Not Found
- 시간 복잡도는
O(logN)이다. (배열(리스트)는 검색 시간 복잡도는O(N)이다.)
배열(리스트)보다 검색(탐색)에 훨씬 효율적이다. 시간 복잡도를 줄이는 데 굉장히 효율적이다.
※ [정리] 트리는 계층적인 관계 표현에 쓰이기 때문에, OS의 FileSystem 구조나 대용량의 데이터를 계층적으로 저장할 때 많이 쓰이는 자료구조가 되겠습니다.
5개의 댓글
안녕하세요 :)
이진탐색트리 설명 중 잘못된 부분이 있는 것 같아 댓글 남깁니다!
right node에는 부모노드와 값이 같거나 큰 값이 저장된다.
=> right node에는 부모노드 값보다 큰 값이 저장된다.
이진탐색트리에서는 중복값이 허용되지 않는 것으로 알고 있습니다!
좋은 글 잘 읽고 갑니다 감사합니다!
The crew's goal is to complete tasks on the spacecraft while trying to track down and eliminate imposters who are quietly creating issues. among us online


안녕하세요, 깔끔한 글 잘 읽었습니다. 혹시 실례가 되지 않는다면 개인 TIL 블로그 포스팅에 순회 이미지를 사용해도 괜찮을까요?