[Push_swap] 그리디 알고리즘 풀이방법 논리 흐름 및 그림 설명
42 Seoul 과정에서 push_swap 과제를 진행하며 생각한 알고리즘을 정리한다. 풀이에 대한 흐름을 그림과 함께 설명해보았다.
과제 설명
- 두개의 스택 A, B가 있을때 프로그램 인자로 받은 수들을 A에 오름차순 정렬시키는 것이 목표이다.
이때 주어진 명령어를 최소한으로 사용하여 정렬하는 프로그램을 만들어야 한다. - 시작 시:
- 스택 a에는 중복되지 않은 양수 및/또는 음수가 무작위로 들어 있다.
- 스택 b는 비어 있다.
명령어 목록 (간단히)
- SA: 스택 A의 맨 위 두 요소를 교환
- SB: 스택 B의 맨 위 두 요소를 교환
- SS: SA와 SB를 동시에 수행
- PA: 스택 B의 맨 위 요소를 스택 A로 이동
- PB: 스택 A의 맨 위 요소를 스택 B로 이동
- RA: 스택 A를 위로 회전
- RB: 스택 B를 위로 회전
- RR: RA와 RB를 동시에 수행
- RRA: 스택 A를 아래로 회전
- RRB: 스택 B를 아래로 회전
- RRR: RRA와 RRB를 동시에 수행
기본 알고리즘으로는 그리디 알고리즘을 적용시켰다. 일단 최적화하는 과정을 생략하고 최대한 논리적 흐름에 맞게 뼈대 알고리즘에 대해 먼저 설명하겠다.
초기 상태
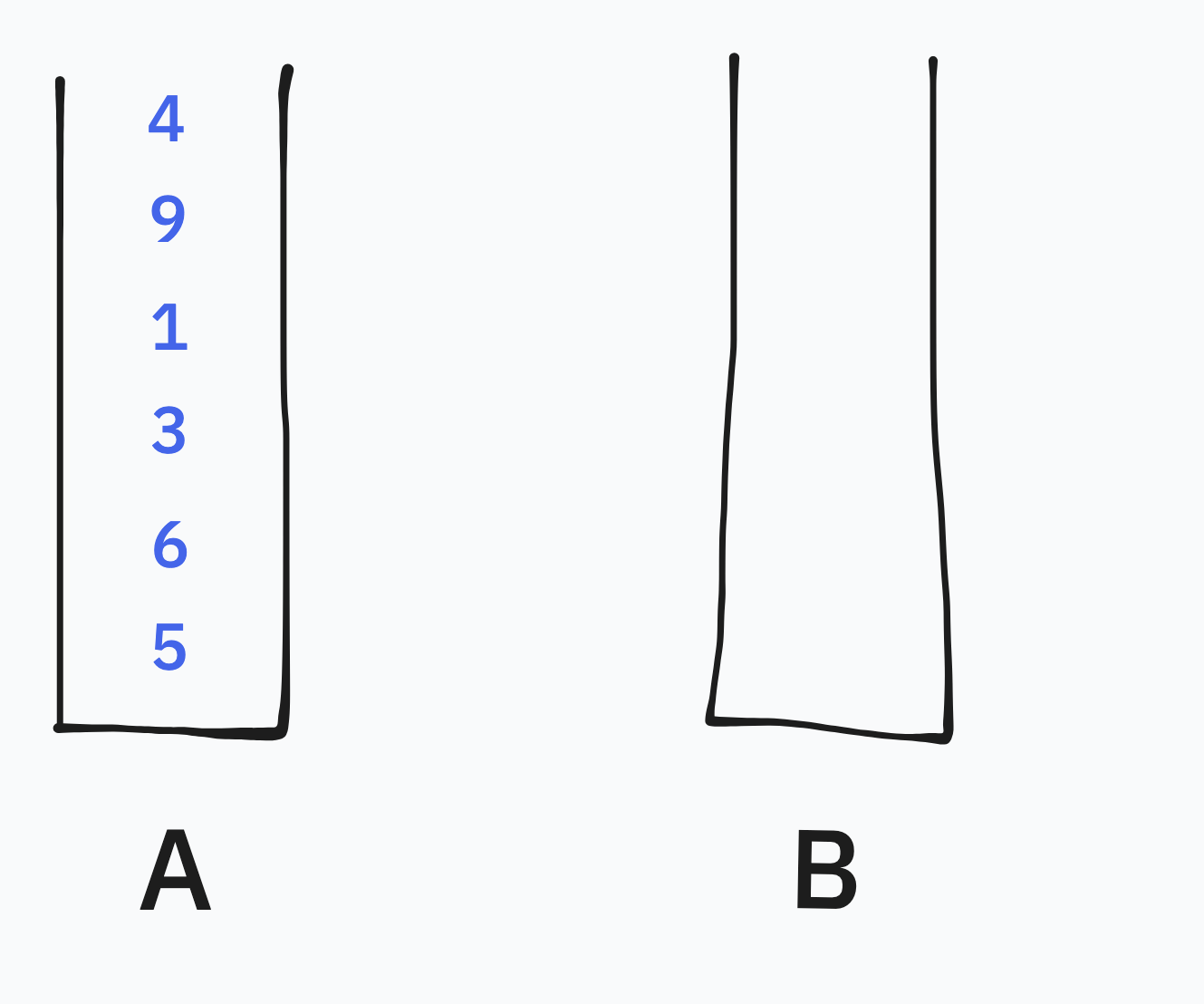
우선 입력 받은 인자들을 스택 A에 저장한 초기 상태는 이와 같을 것이다.
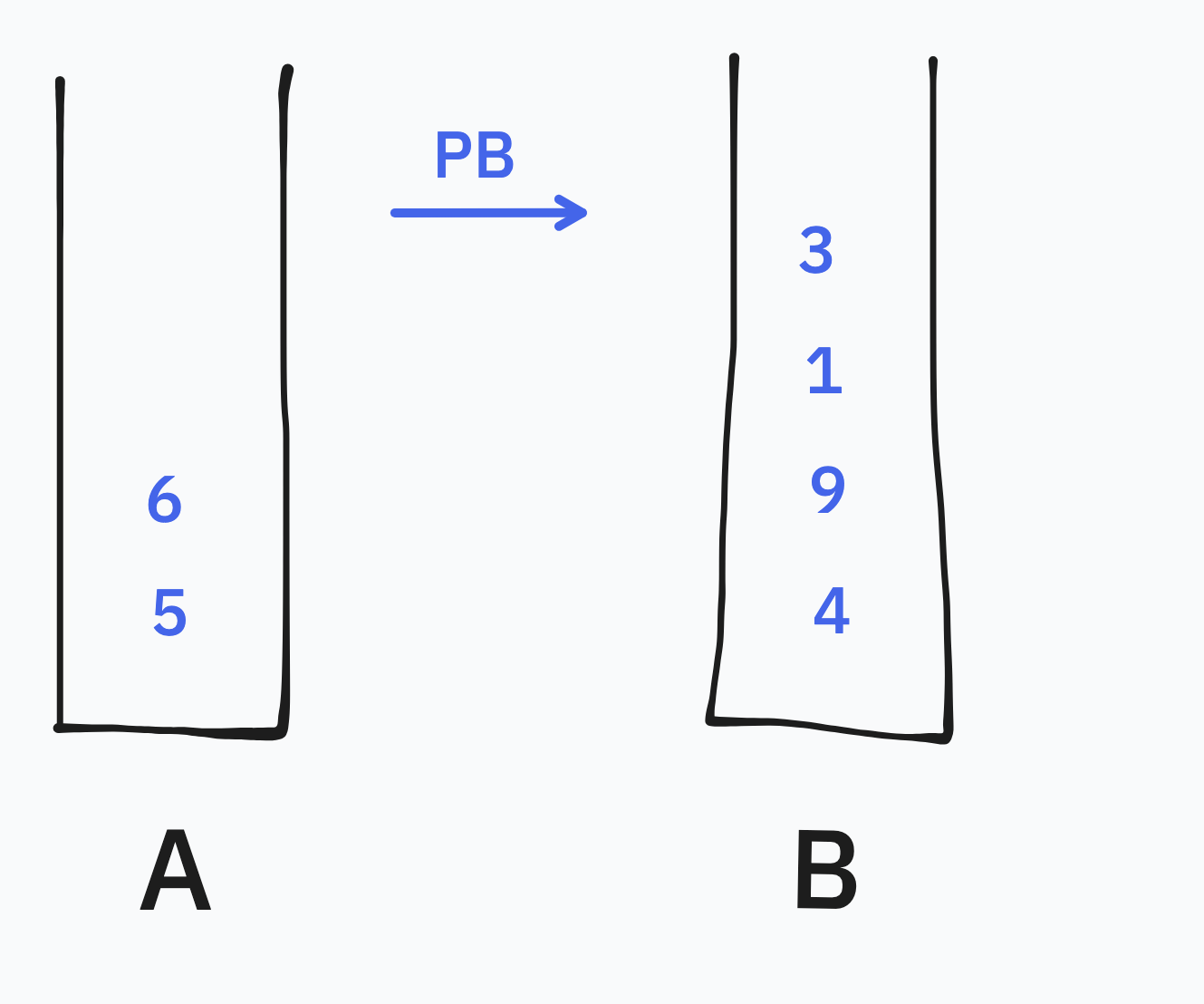
이때 스택 A의 수들을 하드코딩 할 수 있는 수만 남기고 PB로 모두 B로 보낸다.
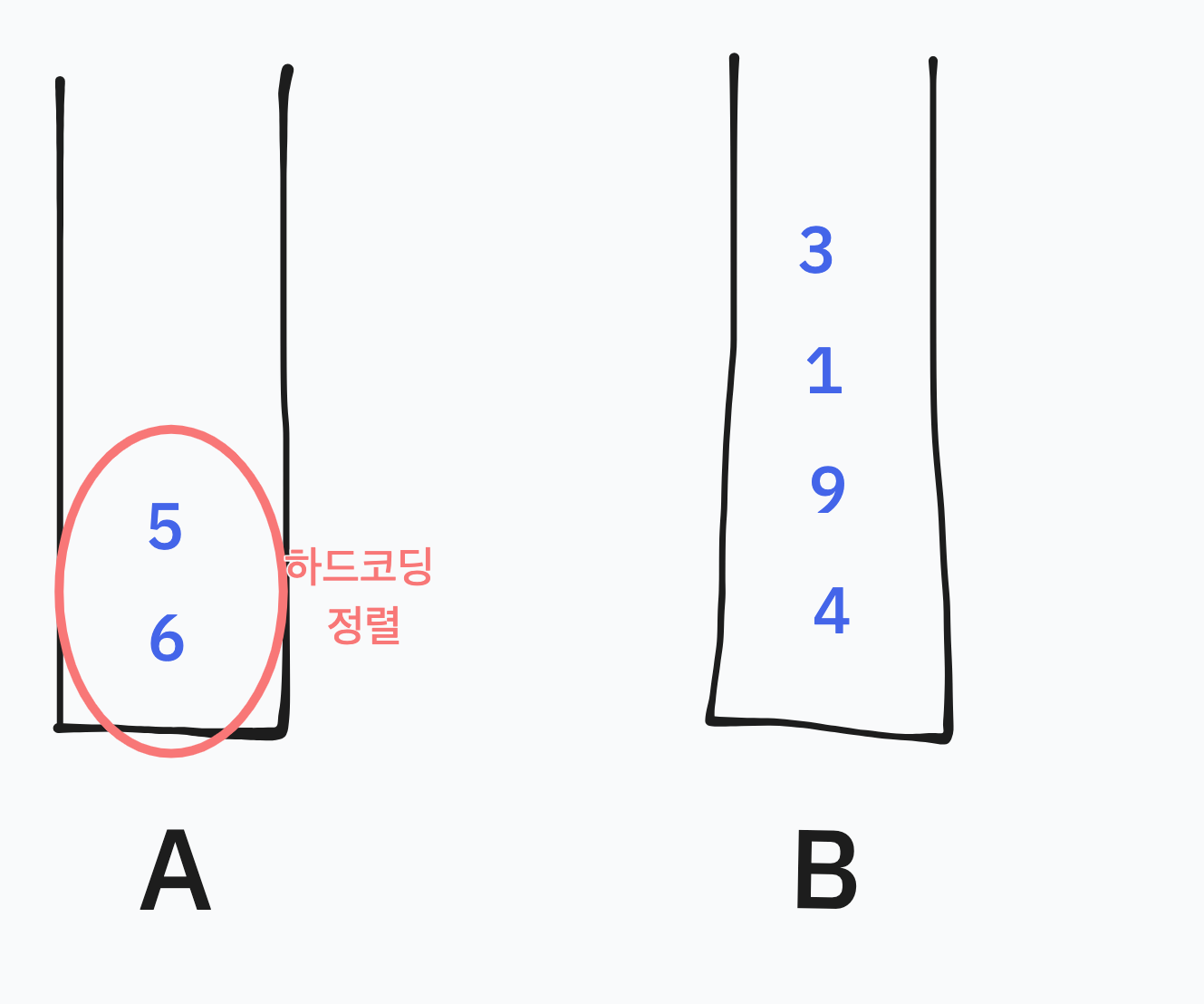
예시에서는 2개만 남기고 B로 보냈다. 실제 구현시 4개나 5개까지 하드코딩을 적용해야 평가를 만점으로 통과 가능했다.
그리디 알고리즘 적용
이후 본격적으로 그리디 알고리즘을 적용시킨다.
그리디 알고리즘은 현재 상황에서 가장 최적의 선택을 하는 풀이를 말한다. 일반적인 알고리즘 문제 풀이에서 그리디 알고리즘을 사용할때는 해당 시점의 최적의 선택이 정말로 마지막 결과에서도 최적의 결과를 도출 하는지 잘 확인해야한다. 이 과정이 굉장히 어렵고 쉽게 보이지 않기 때문에 그리디 알고리즘을 사용하는 것은 조심해야한다.
하지만 push_swap 과제에서는 가장 적은 명령어를 쓰는 최적의 시나리오(하나의 정답)를 찾는 것이 아니고 평가 기준에 부합하는 충분히 적은 명령어로 정렬을 하면 되기 때문에 그리디 알고리즘에 대한 증명없이 일단 적용을 시키고 이 방법이 충분히 효과적이라면 정당성은 입증된다고 생각했다. 👊
그렇다면 이 과제에서 그리디를 어떻게 적용 할 수 있을까?
바로 현재 상황에서 B의 모든 수에 대해 탐색을 진행하는데, 어떤 수 하나를 A로 보내 오름차순을 만들때 필요한 최소의 명령어를 사용하는 수를 찾는 것이다.
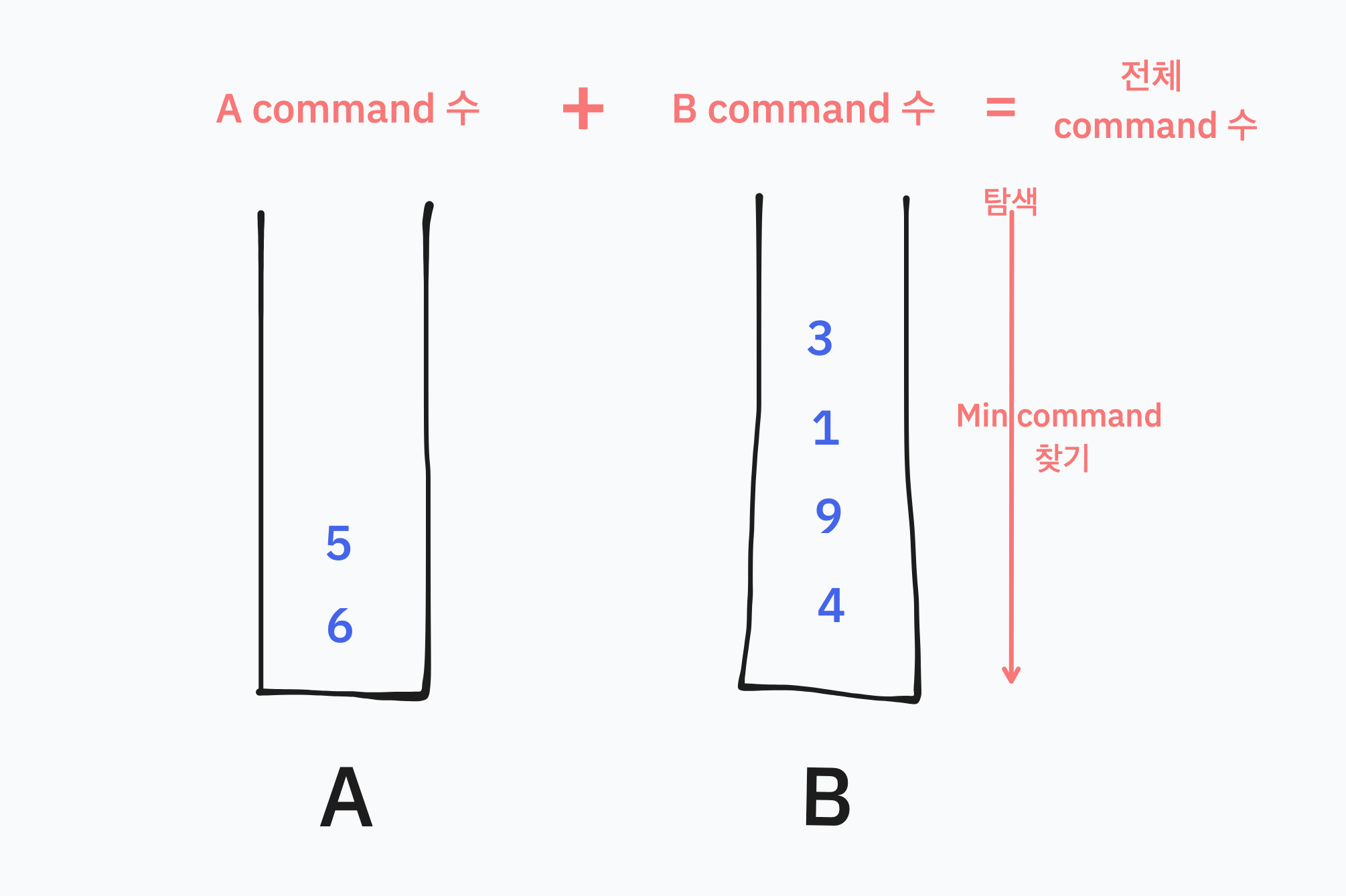
이때 A에서 사용되는 명령어가 있고 B에서 사용되는 명령어가 있을 것이다. 아직까지 A와 B에서 사용되는 명령어라는게 어떻게 구해지는 감이 잘 안 올 것이다.
A 에서의 명령어 수
먼저 A의 상황을 보자.
일단 어떤 수가 B에서 PA로 보내질때 우리는 A의 상태를 항상 오름차순으로 유지한다는 조건을 추가할 것이다.
그래야만 B에 있는 모든 수를 보냈을때 A를 오름차순으로 정렬 할 수 있기 때문이다.
예시를 들어 설명해보자.
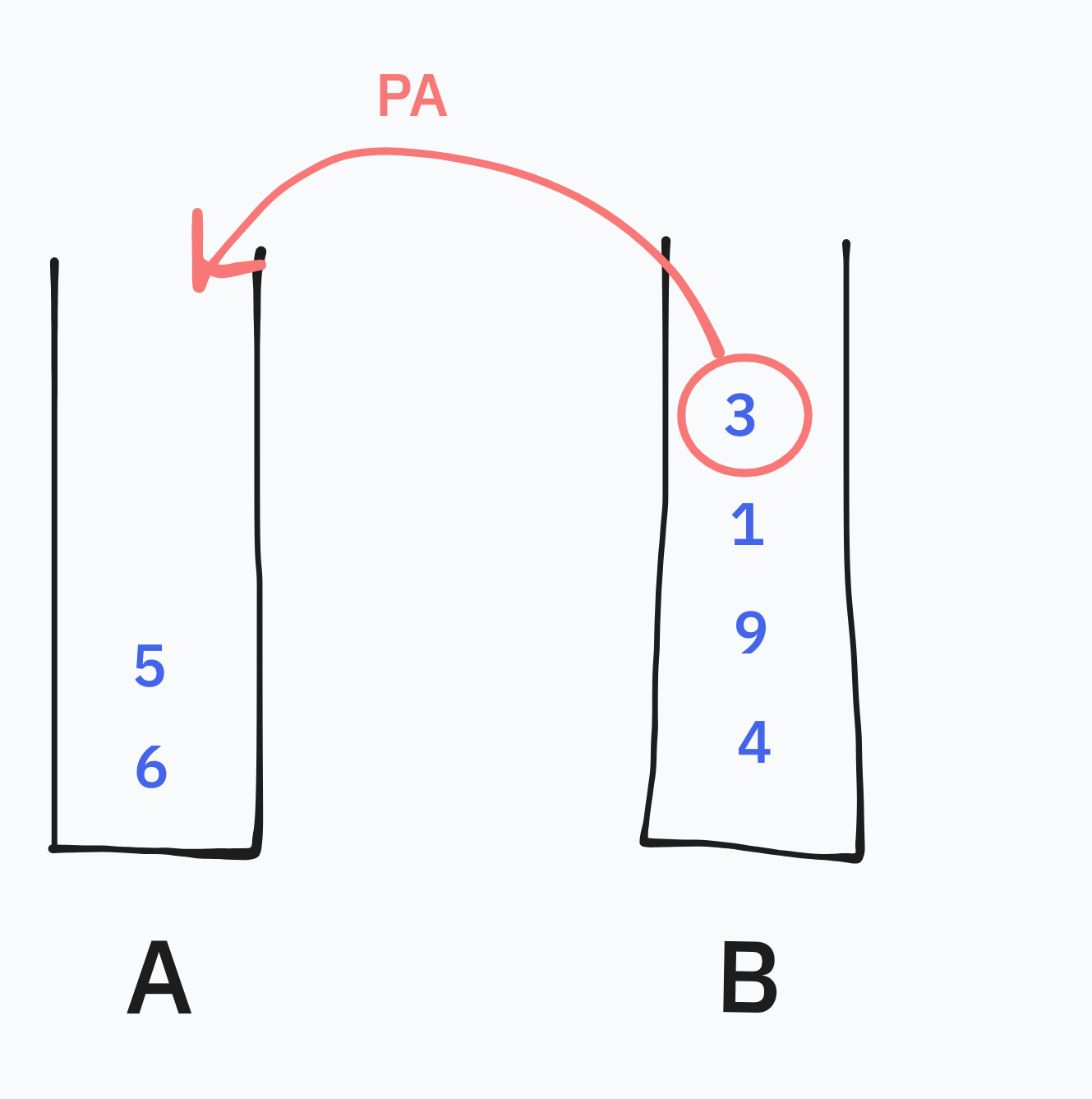
A가 다음과 같이 정렬된 상황에서 B에서 3이 보내진다고 생각해보자.
이 경우 A는 그냥 3을 그대로 받아도 오름차순을 유지할 수 있으므로 A에서 사용해야하는 명령어는 0개가 된다.
다른 예시를 들어보자.
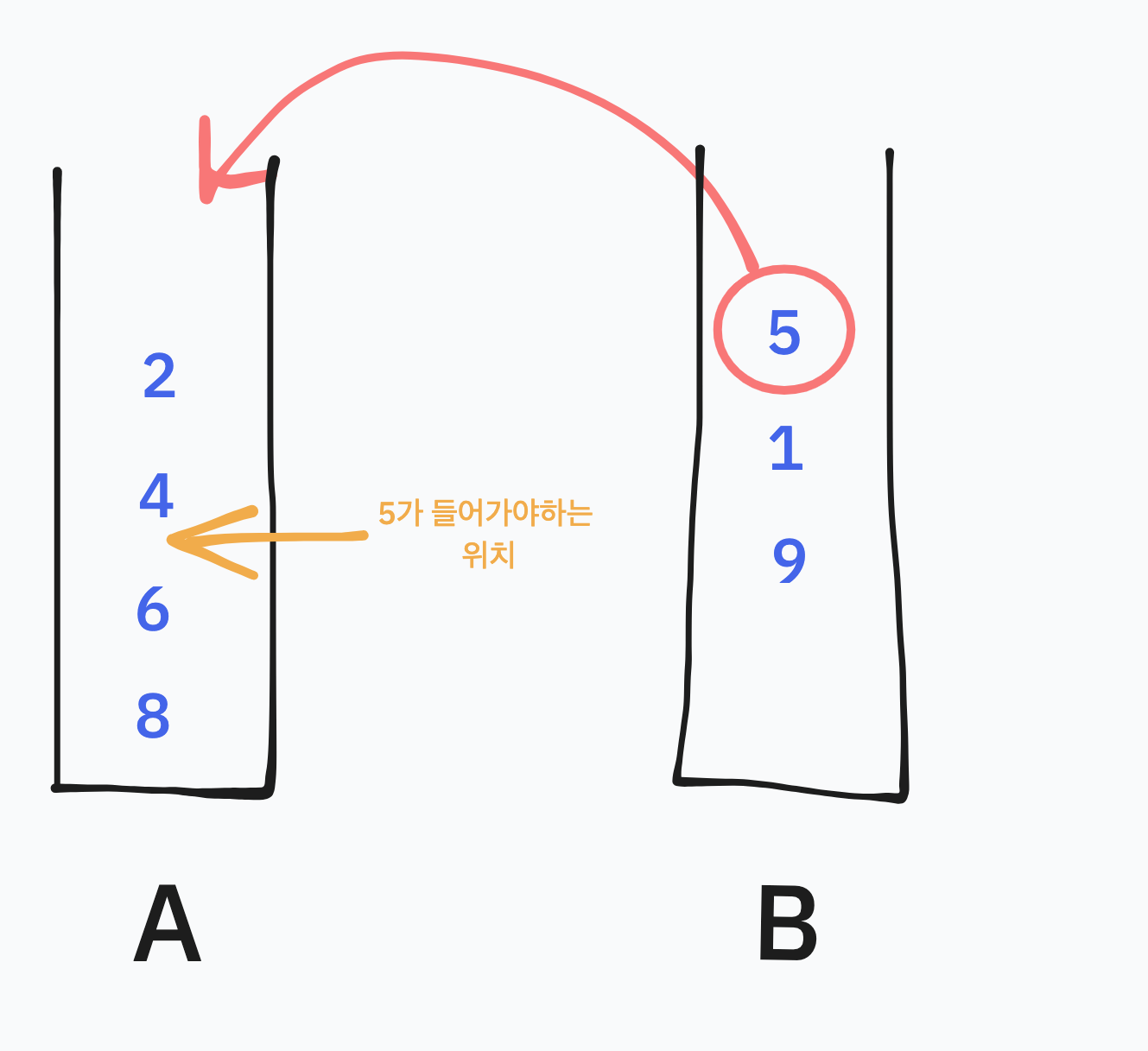
만약 B에서 보내지는 수가 5일때 A가 오름 차순을 유지하려면 어떻게 해야할까? 5는 현재 A에 있는 수들의 중간에 위치해야하므로 A를 어떤 식으로든 명령어를 써서 5를 받기 위한 형태로 바꿔야한다.
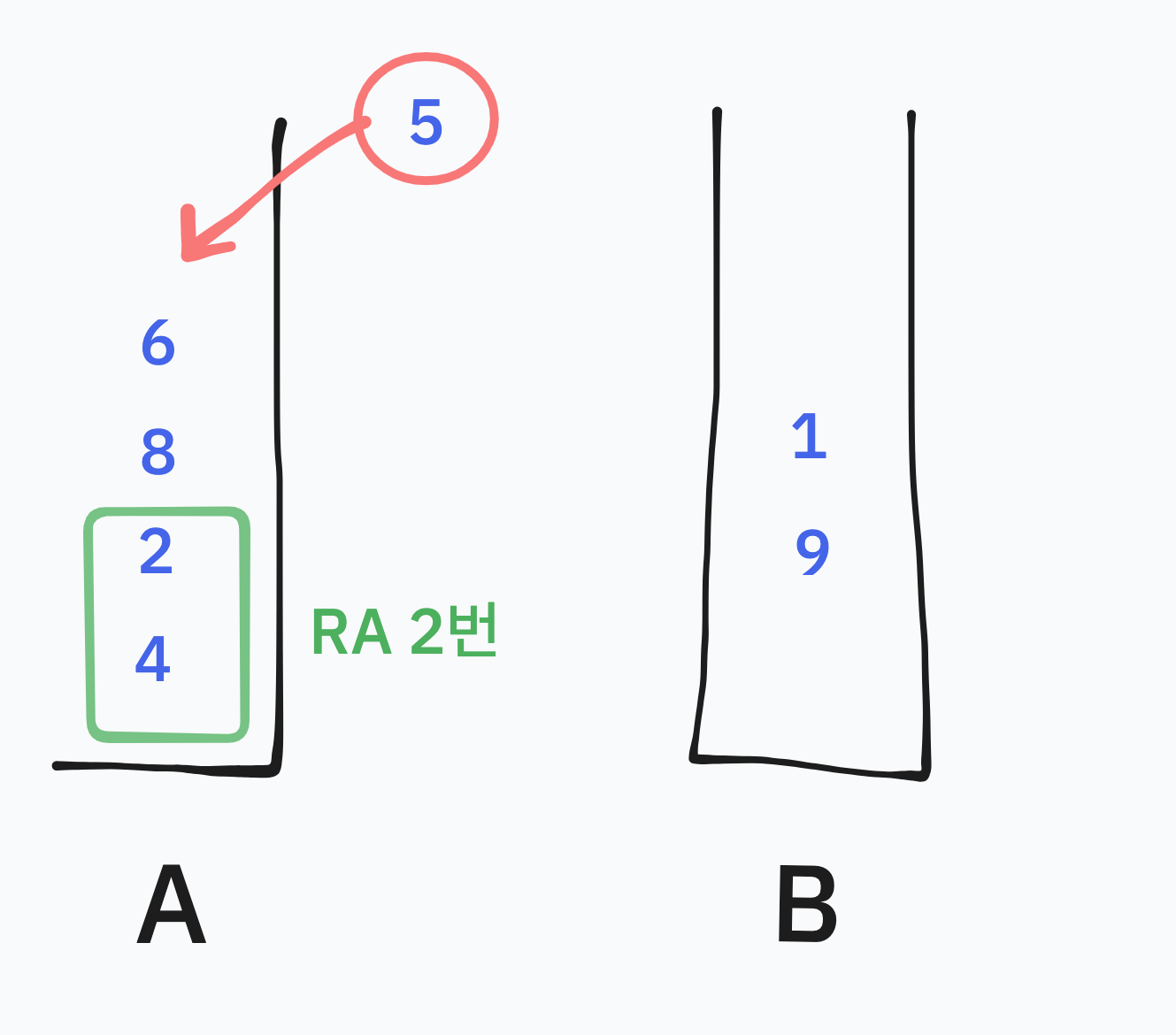
이때 A에서 5보다 작은 수들을 RA로 돌려준다면 5를 A의 Top으로 받았을 때 그림과 같이 오름차순이 두번 있는 형태 [5,6,8], [2,4] 로 받을 수 있게 된다.
이때 A를 다시 하나의 오름차순으로 바꿔줘야하지 않나 생각 할 수 있는데 굳이 B의 어떤 수를 받는 매과정에서 하나의 오름차순으로 다시 만들어주는 것은 불필요하게 명령어를 쓰는 것이라고 생각했다. 하나의 오름차순으로 다시 만든 후에 받는 수가 다시 A의 중간에 오는 수가 오면 다시 그만큼 RA를 써서 그 수를 top으로 받을 수 있게 해야하기 때문이다.
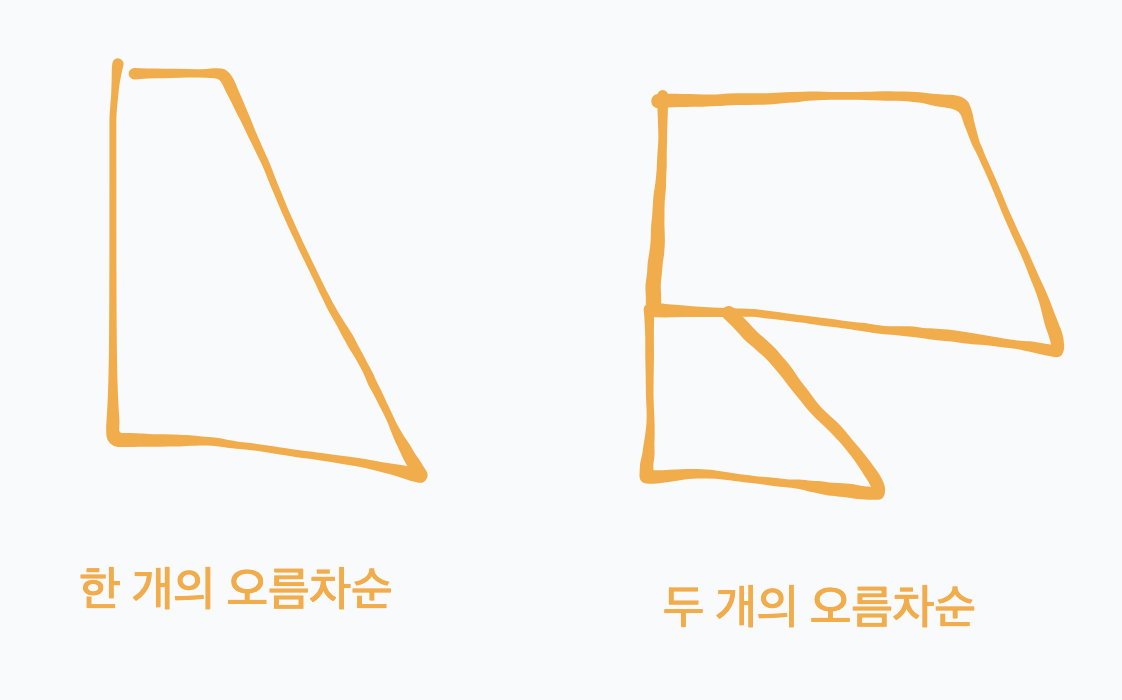
즉 A는 이와 같이 오름차순이 두번 나타나는 형태 또는 그냥 오름차순이 하나인 형태로 존재하게된다.
그리고 어떤 수를 A가 받을 때 A가 사용하는 명령어는 위에서 말한 A의 오름차순 조건을 유지하면서 그 수를 Top으로 받기 위해 사용하는 명령어 개수라고 할 수 있다. 이때 A를 RA 또는 RRA를 사용해서 위치를 조정하면 되고 그 기준은 받는 수의 위치가 현재 A의 index에서 절반 이하면 RA, 절반을 넘으면 RRA로 돌리는게 더 적은 명령어를 사용할 수 있게 된다.
B 에서의 명령어 수
이제 어떤 수를 선택했을 때 B에서 사용하는 명령어의 수를 계산해보자. B에서 사용하는 명령어는 굉장히 간단하다. 단지 그 수를 B의 Top으로 보내고 PA를 하면 되기 때문이다.
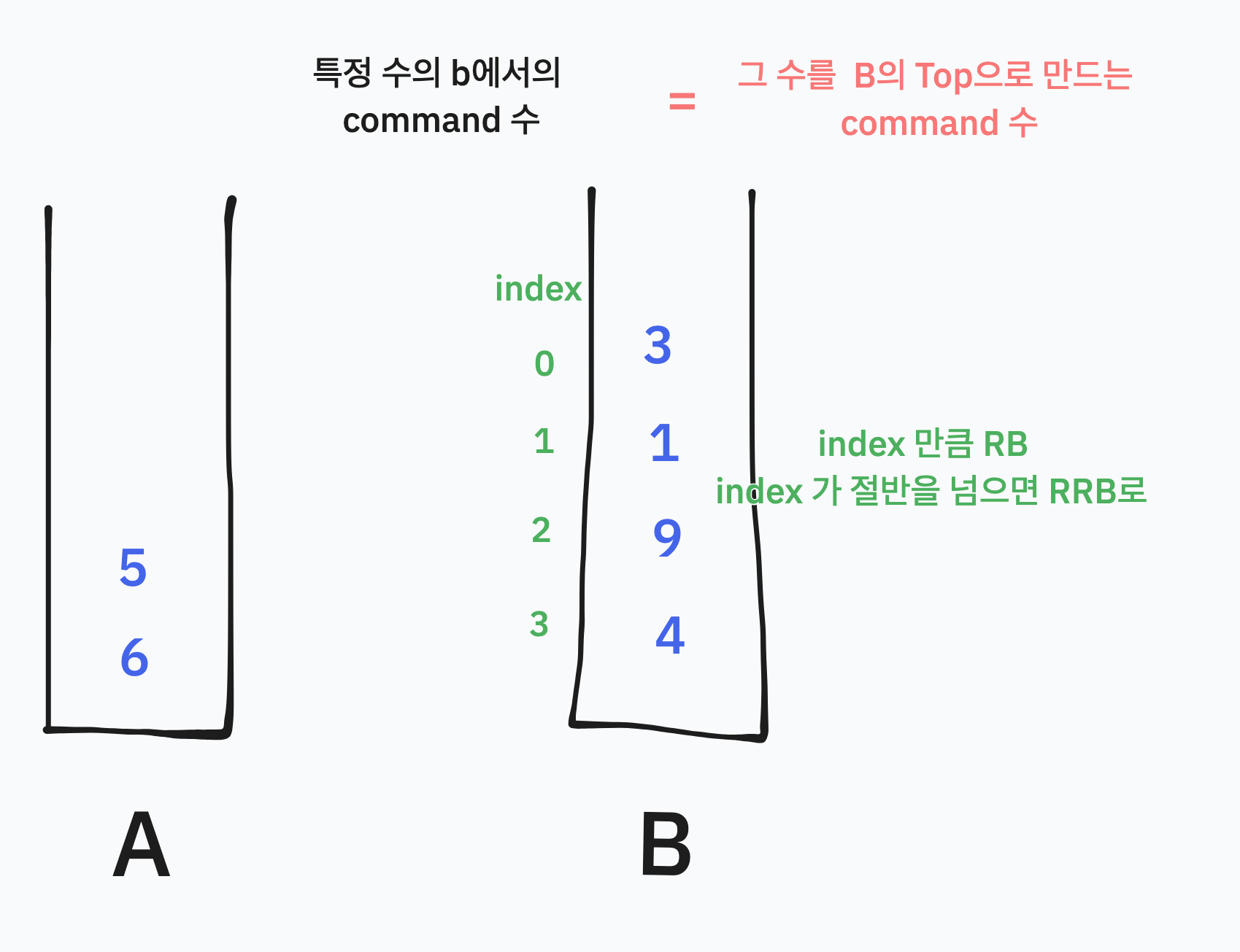
즉 위와 같이 index가 있으면 어떤 수를 top으로 보내는 명령어수는 그 수의 B에서의 index만큼 RB를 하면 된다. 여기서 마찬가지로 index가 절반을 넘으면 RRB로 Top으로 보내는게 더 적은 명령어를 쓰게 된다.
결국 B에 있는 어떤 수를 A로 보내는 명령어 수는 지금까지 설명한 A에서의 사용명령어 + B에서의 명령어 + 1(PA)이다.
반복 및 마지막 상태 체크
자. 이제 핵심적인 내용은 모두 끝났다.
결국 현재 상황에서 이렇게 구할 수 있는 전체 명령어 수가 가장 적은 수를 B에서 탐색하고 그 수를 저장해놓은 명령어 대로 동작시키면 된다. 이 동작을 B의 사이즈가 0이 될때까지 반복하면 결국 모든 수는 A에 오름 차순 형태로 존재하게된다.
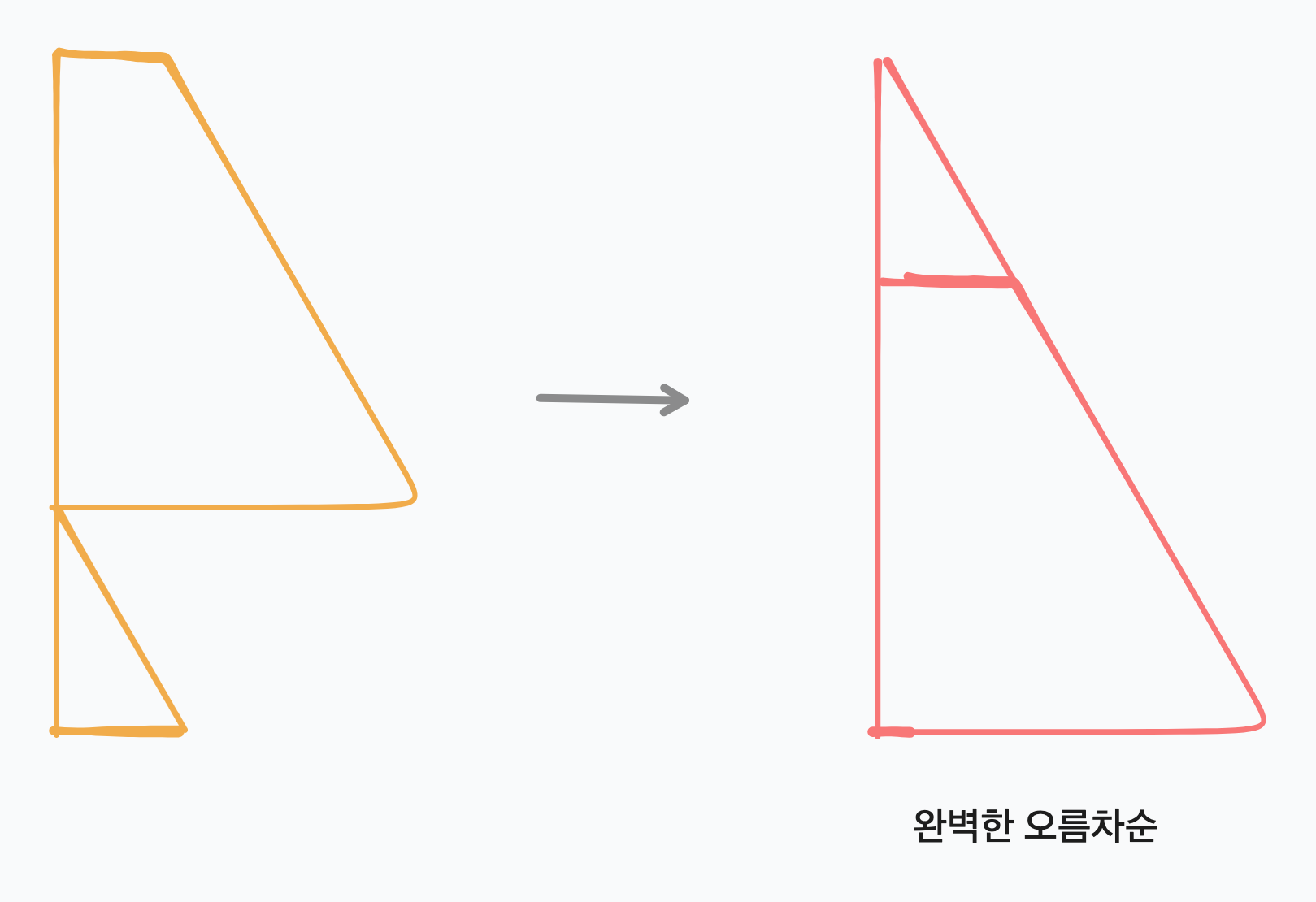
이때 마지막에 A의 상태가 두개의 오름차순이 존재하는 상태일 수 있으므로 그 상태인지 체크하고 하나의 완벽한 오름차순으로만 만들면 된다. 굿!
여기까지 잘 따라왔다면 아마 드디어 감이 잡히고 구현하는데 큰 문제는 없을 것이다.
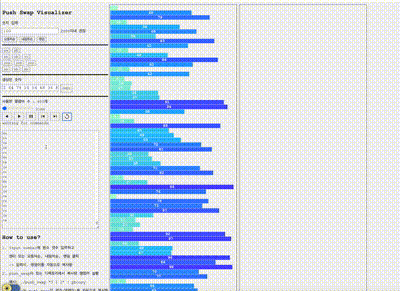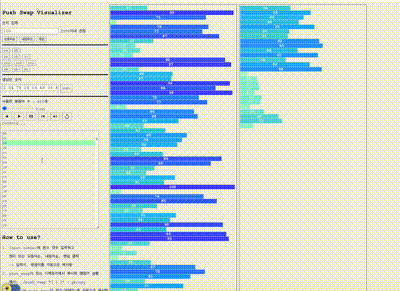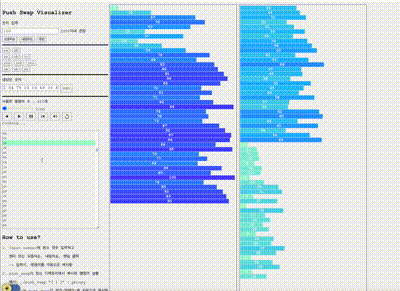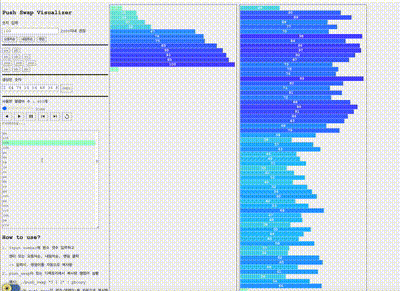
테스팅
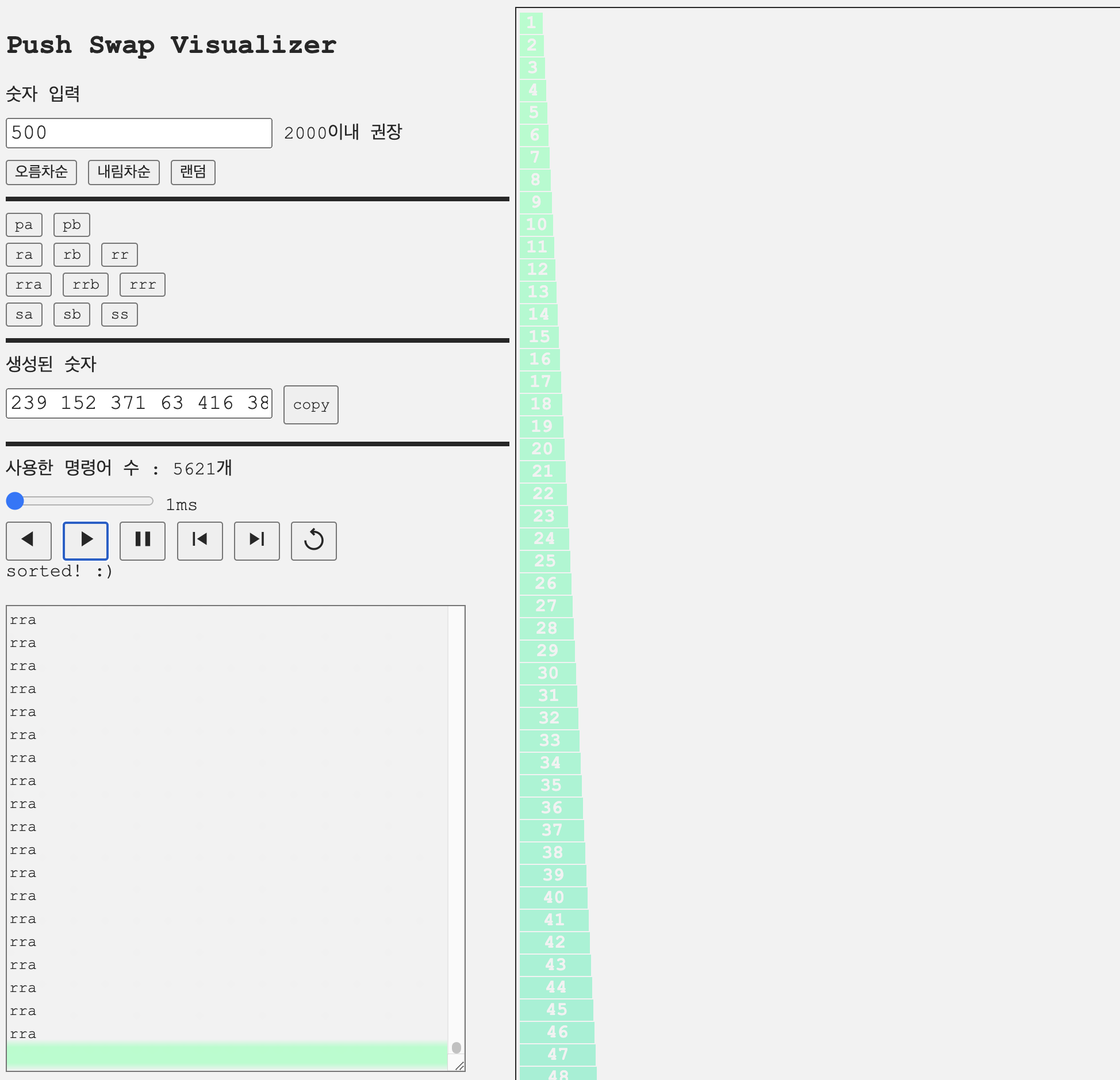
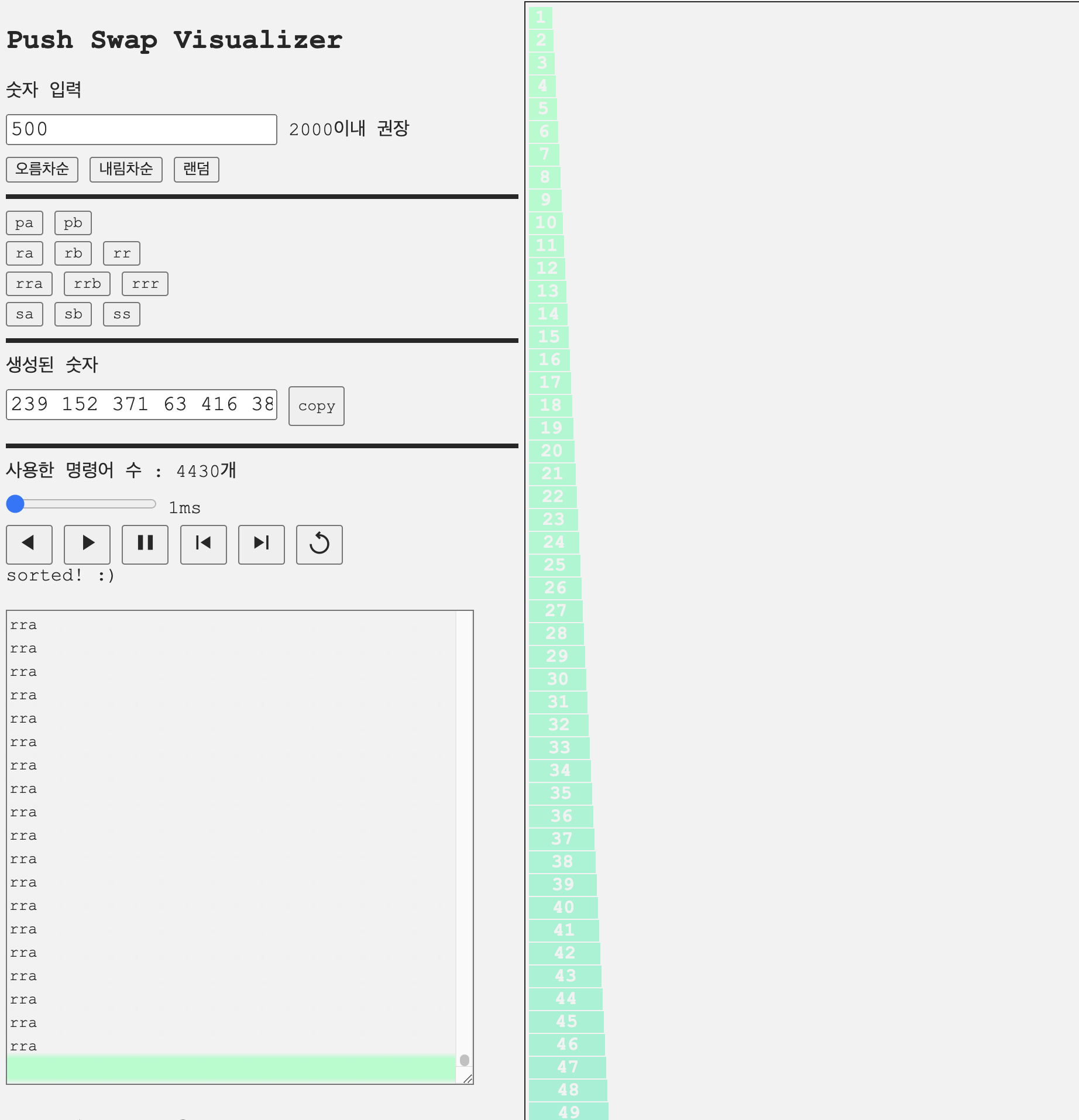
위와 같이 구현후 인자 500개에 대한 테스트를 push swap visualizer로 확인해보았다.
만점으로 통과하는 케이스도 있지만 명령어 수가 5500개를 넘는 케이스가 있었다.
최적화
여기서 어떻게 해야 더 최적화가 가능할까 생각해보았다.
visualizer를 보면 B에 존재하는 수들의 크기가 들쭉날쭉으로 순서대로 위치하다보니 그리디에서 매번 A로 보내겠다고 선택하는 수의 크기들도 작았다 컸다 하면서 A에서 스택을 돌리는 명령어가 많이 사용되는 것 같다고 생각했다.
따라서 B에서 매번 비슷한 크기의 수가 A로 보내지면 명령어를 줄일 수 있지 않을까라는 생각을 하였다.
이를 위해 A에 모든 수가 있는 초기 상태에서 B로 수들을 보낼때
특정 pivot값을 기준으로 큰 수는 PB, 작은 수는 PB, RRB를 하면 B에서 수들이 같은 범위의 수들이 군집을 이룬 상태로 존재하고
이런 상태가 B에서 보내는 수를 선택할때 비슷한 범위의 수들을 A에 보내어 명령어가 많이 줄어들지 않을까 생각했다.
이때 우선 각 군집 크기를 가장 비슷하게 적절히 나눠야 좋은 성능을 낼 수 있을 것이기 때문에 군집을 나누는 기준인 pivot 수를 처음 받은 수들을 선정렬한 후 구해주었다.
구현할때는 미리 정렬한 배열의 1/3, 2/3 index의 수를 pivot으로 두개를 잡았다.
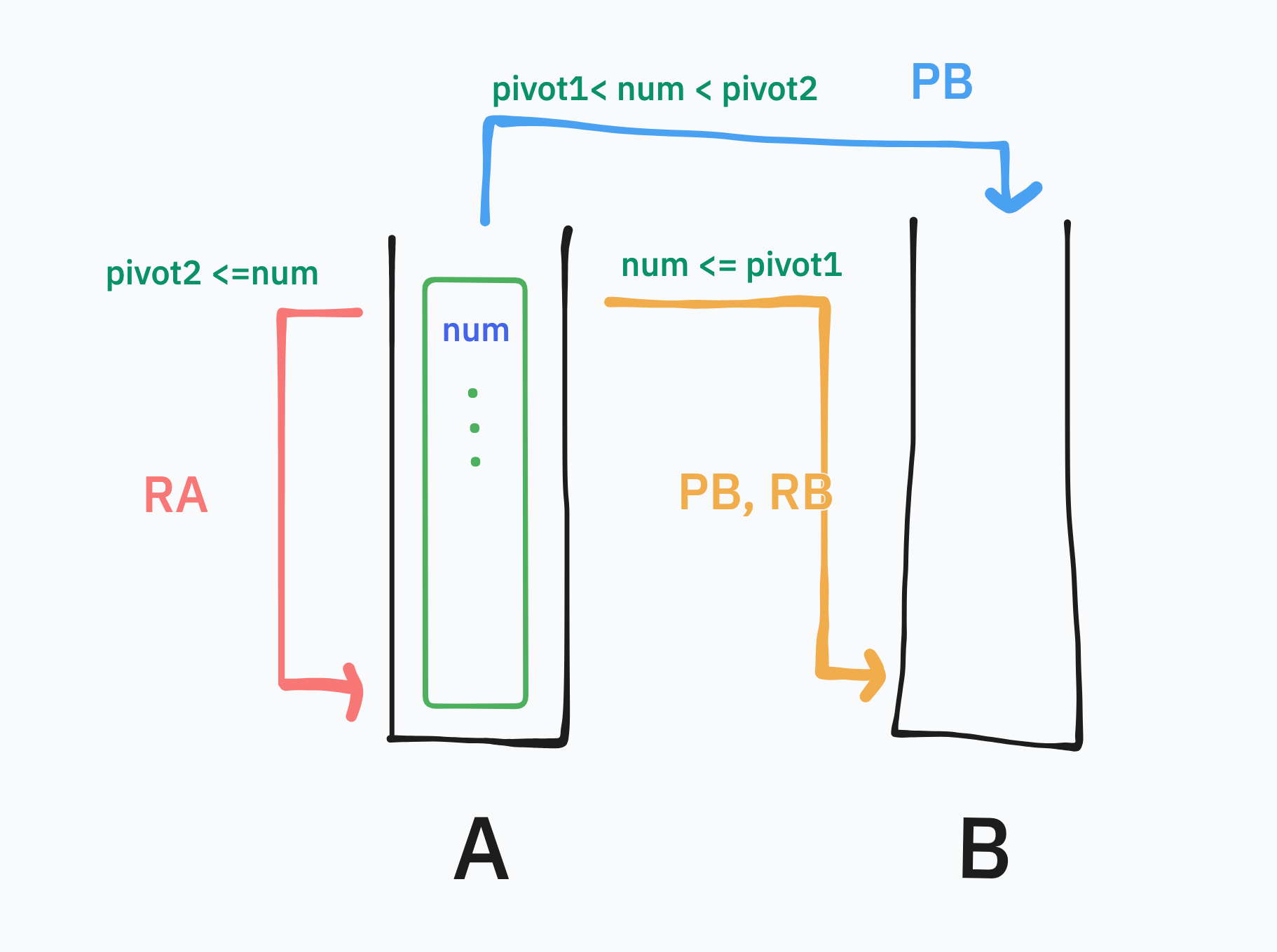
위와 같이 두 pivot값을 기준으로 A에 있는 수들을 군집화를 진행한다.
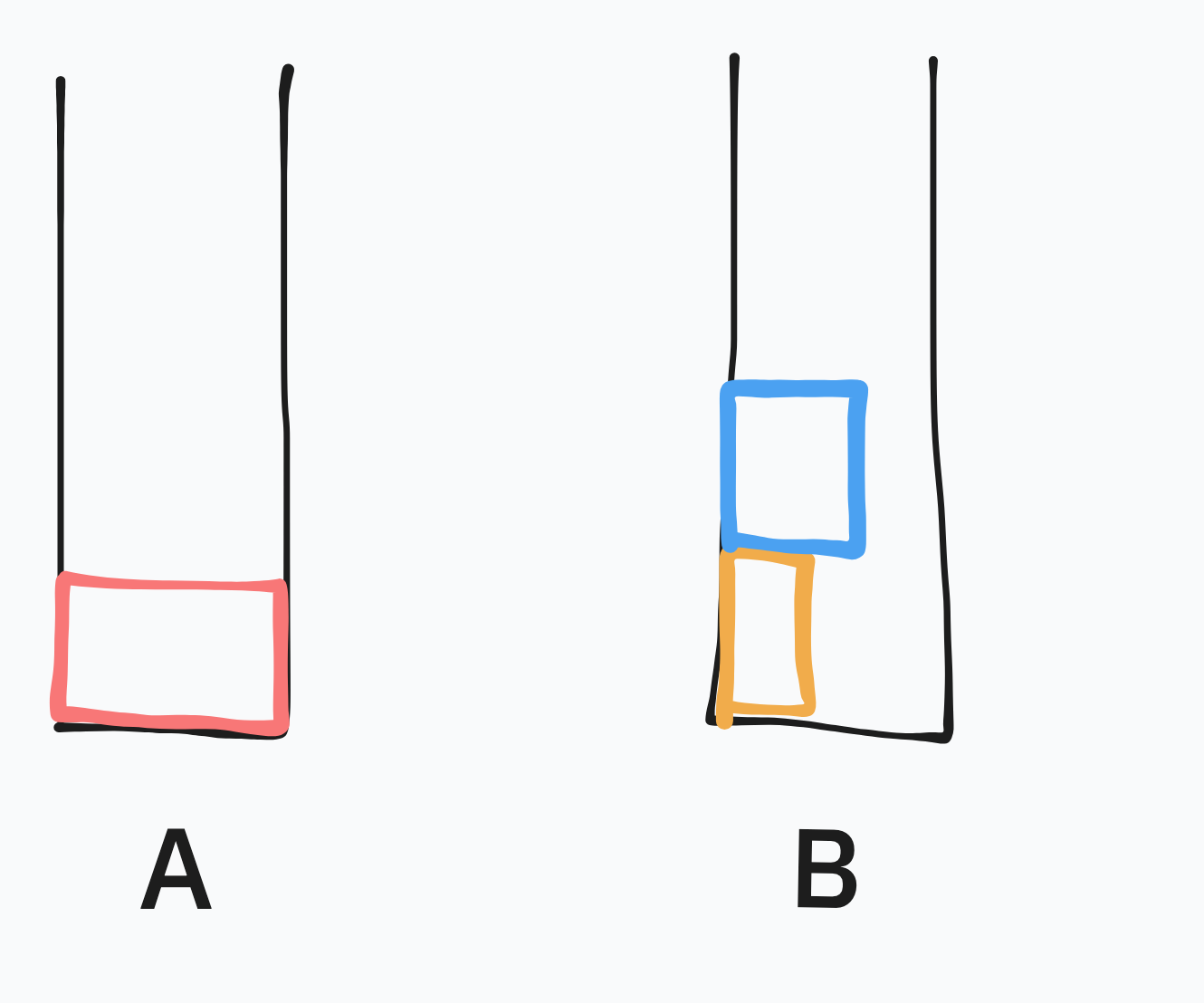
위와 같은 수의 크기로 값들이 군집화 되게 된다.
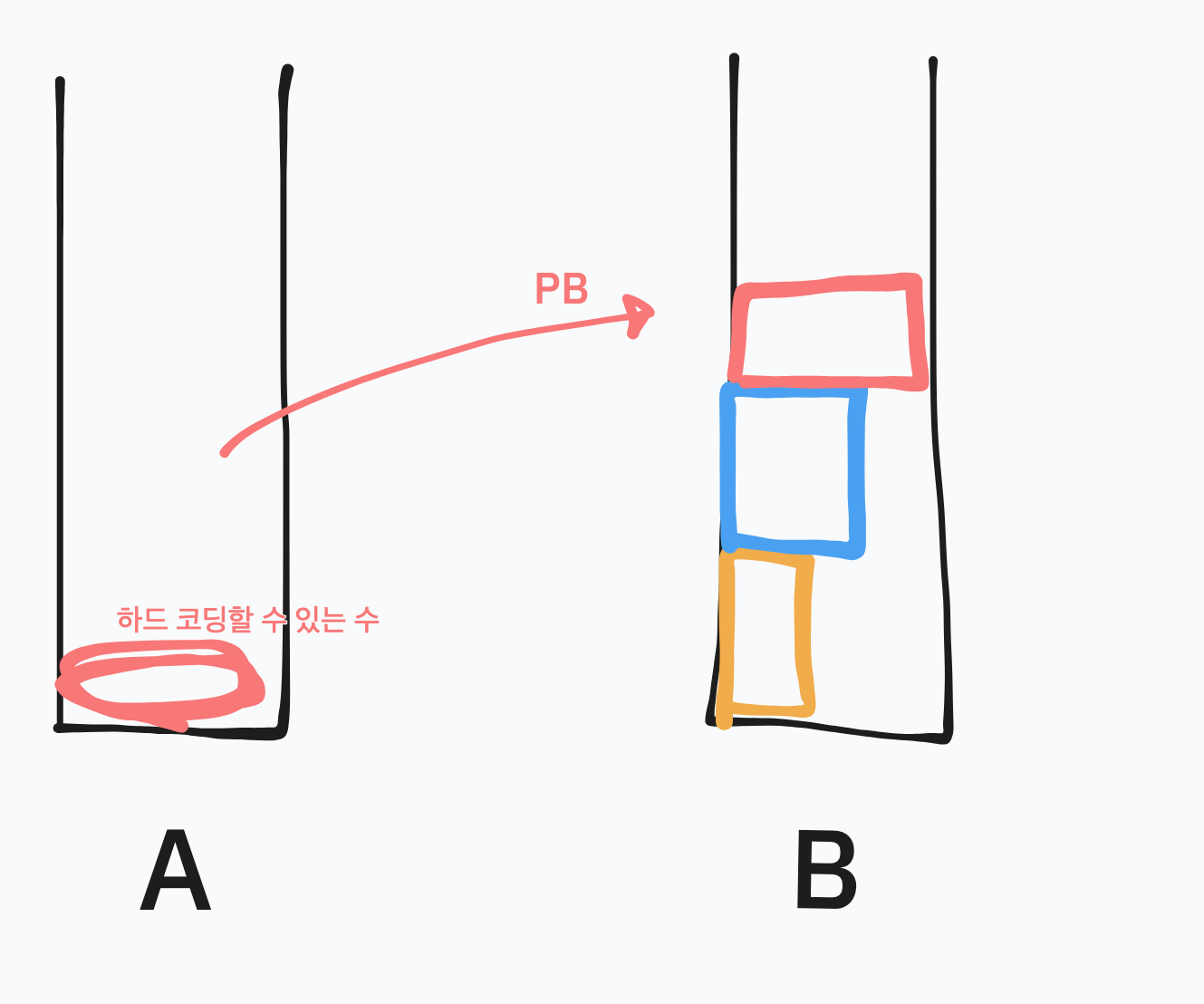
이후 마지막으로 A에 있는 수들을 하드코딩할 수 있는 수만 남기고 B로 보내주었다.
위 상태에서 앞선 그리디 방법을 적용해본 결과 명령어 수가 500개 기준으로 20% 가까이 줄어드는 것을 확인 할 수 있었다.
회고
처음에 과제가 일반적인 알고리즘 problem solving과는 다르게 시간복잡도를 고려하지 않고 정답이 있는 문제도 아니여서 풀이를 어떤 식으로 가져가야할지 고민이 많이 되었던 것 같다. 또한 명령어 파싱의 에러처리 부분과 유효한 인자를 어떤 자료구조에 저장하는게 좋을지 생각하고 코드로 구현하며 배열과 리스트의 차이와 특징을 정리할 수 있었다. 과제의 조건은 아니였지만 시간복잡도와 공간복잡도를 고려한 효율적인 코드를 짜려고 최대한 고민했던 것 같다.
최적화 과정을 진행하면서는 quick sort의 pivot 개념을 적용시켰는데 성능이 효과적으로 나타나 만족스러웠으며 역시 모든 SW에서 최적화 과정이 필수적이라는 것과 이를 통해 성능 개선을 하는 것이 얼마나 중요한지 몸소 느낄 수 있었다.
고생했다!👊