Map-reduce

Map-Reduce engine?

• A Map Reduce engine refers to the software or framework that implements the Map Reduce programming model for processing and analyzing large datasets in a distributed and parallelized manner.
• A map reduce engine automatically paralleizes and distributes the execution of the mapper and reducer functions that charcterize an application.
• It is highly fault tolereant.

Programming model (Paradigm)

• Functional programming approach

1. map

• mapper function is fed one key-value pair and generate the list associated to output value.
• The results of the map phase are hased by key, and written to the store(barrier). The hash divides the map output into 1 bucket per reducer (mod num_of_reducer)
• The engine waits for the map phase on a node to finish (bottle neck point).

input: (in_key, in_value)
output: (out_key, intermediate_value) list

2. reducer

• Reducer pull the relevant data from the all different mapper nodes.
• Reduce phase cannot start until the map phase has completed on all nodes.

input: (out_key, intermediate_Value list)
output: out_value list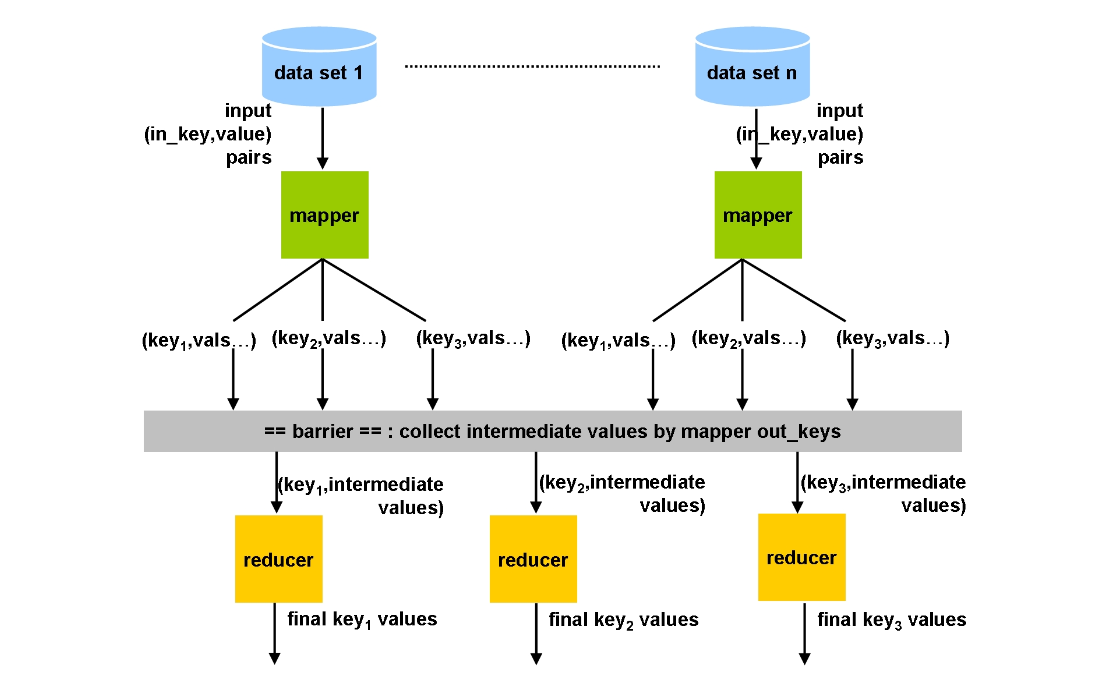

Example: Word Counting

map(String input_key, String input_value)
 // input_key: document name
 // input_value: document contents
 for each word w in input_value:
 	EmitIntermediate(w, "1");

reduce(String output_key, Iterator Intermediate_values)
  // output_key: a word
  // output_values: a list of counts
  int result = 0;
  for each v in intermediate_values:
  	result += ParseInt(v);
  Emit(AsStirng(result));

Map-reduce semantics for Relational Algebraic Operator

1. Selection

• Selection is capture by the mapper alone, reducer is just the identity function.

• For $\sigma_c(R)$

  Map: For each t in the input, if C(t) is true, then emit the key-value pair (t, t), i.e., set both key and value to t.
  Reduce: For each (t, t) from any of many mappers, emit (t, t).

• The key is hashed to be distributed to reducers.

2. Projection

• Under set semantics, projection must eliminate duplicates.
• For $\pi_A(R)$, where $R$is the single input relation to the mapper and $A$ isthe se of columns.

Map: For each t in the input, construct t a tuple t' containing only the columns in A and emit the key-value pair (t', t'), i.e., set both key and value to t'.
Reduce: For each t' from any of many mappers, there will be one or more (t', t') pairs (i.e., the reducer takes pairs of the form (t', [t', t', ... , t']), emit exactly one pair (t', t') for each key t' for deduplication.

3. Union

• Union has a merely formatting mapper and a duplicate-eliminating reducer.
• For $R \cup S$ where $R$ and $S$ are the input relations, we define:

Map: For each t in the input, emit the key-value pair (t, t), i.e., set both key and value to t.
Reduce: For each key t from any of many mappers, there will be one or two (t, t) pairs (i.e., the reducer takes pairs such as (t, [t]) or (t, [t, t]), emit exactly one pair (t, t) for each key t.

4. Intersection

• Similar to the Union
• For $R \cap S$ where $R$ and $S$ are the input relations.

Map: For each t in the input, emit the key-value pair (t, t), i.e., set both key and value to t
Reduce: For each key t from any of many mappers, there will be one or two (t, t) pairs (i.e., the reducer takes pairs such as (t, [t]) or (t [t,t]). If second element is a singleton, emit nothing, otherwise emit exactly one pair (t, t) for each key t.

5. Difference

• The information as to which relation the tuple is from needs to be passed on to the reducer.
• For $R$ \ $S$ where $R$ and $S$ are the input relations.

Map: For each t in the input, if t $\in$ R, emit the key -value pair (t, 'R'), other wise emit the key-value pair (t, 'S'), where the second element may be implemented economically with a single bit to indicate membership in either of the two input relations.
Reduce: For each key t from any of many mappers, if the associated value list is ['R'], then emit exactly one pair (t,t) for each key t, otherwise emit nothing.

6. Natural Join

• For $R \bowtie S$, where $R$ and $S$ are the input relations with schemas (A, B) and (B, C).

Map: For each t in the input, if t $\in$ R, emit key-value pair (b, ('R',a)), otherwise emit the key-value pair (b, ('S', c)), where a, b, c are values in the columns A, B, C, rep..
Reduce: For each key b from any of many mappers, the associated value list will be contain pairs of the form ('R', a) or ('S',c ). Then compute

for each key b
	list = []
    for each ('R', a)
    	for each ('S', c)
        	list.append((a, b, c))
    emit(b, list)

7. Partitioned Aggregation (Group-By)

• Consider the concrete example of a relation $R(A, B, C)$ to which we apply the operation $A\gamma_\phi(B)$ where $\phi$ is a an aggregation function, $B$ the column being aggregated, and $A$ the grouping column.

Map: For each tuple (a, b, c) in the input, emit the key-value pair (a, b), i.e., the grouping attribute is the obvious key and, under map-reduce semantics, the desired partition of the input follows from that.
Reduce: For each key a from any of many mappers, there will be one or more (a, b) pairs (i.e., the reducer takes pairs of the form (a, [b1, b2, ..., bn])), emit exactly one pair (a, x) for each key a, where x = $\phi$([b1, b2,..., bn]) (e.g., if $\phi$ is Sum, then x = b1+ b2+ ... + bn)