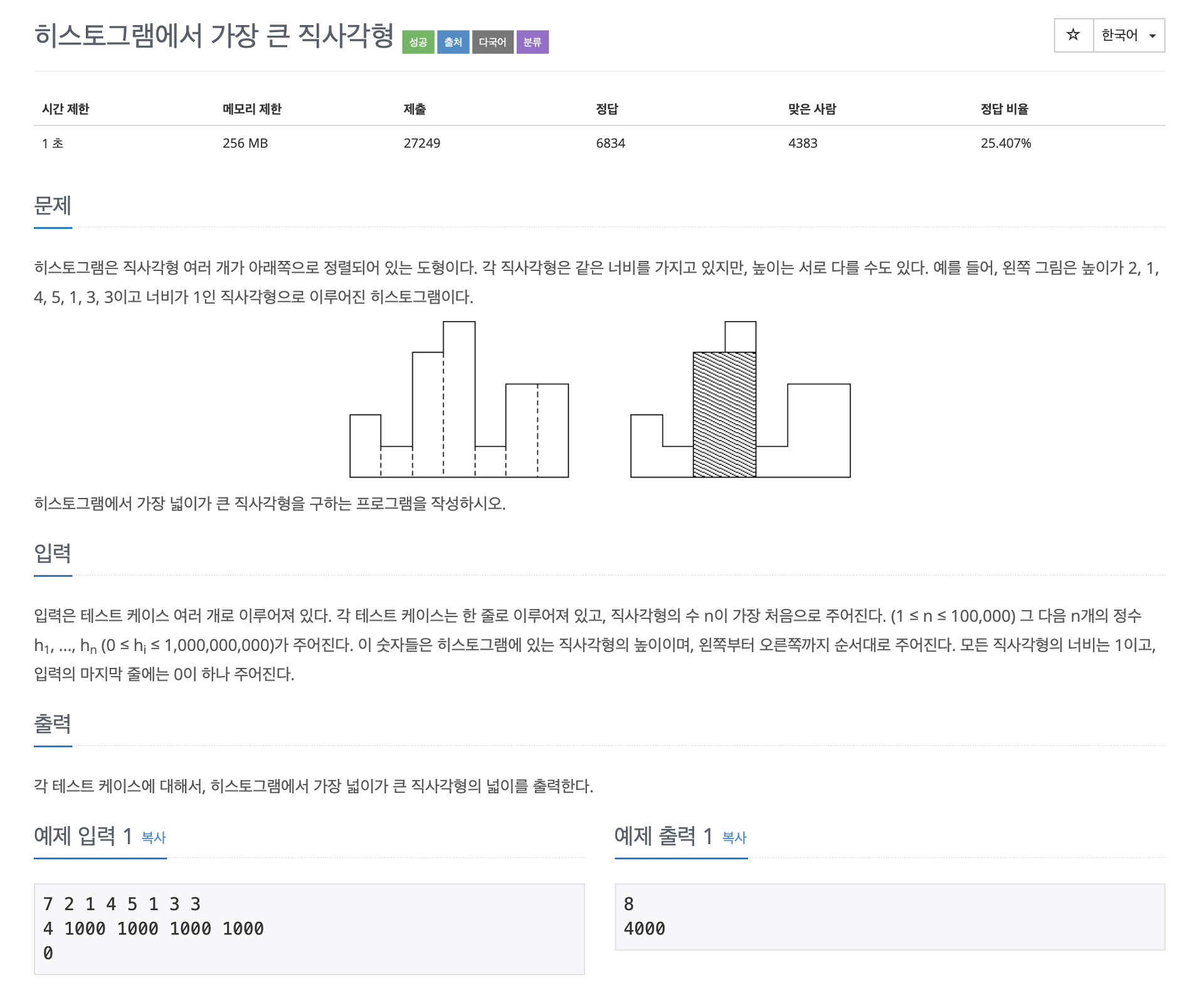
해결 방법
https://st-lab.tistory.com/255
막히면 항상 찾아보는 블로그.. 오늘도 감사합니다!
알고리즘
이번 문제에 해결 방법에는 크게 2가지가 있었다.
분할정복과 스택 자료구조를 이용한 풀이방식이다.
(나중에 세그먼트 트리에 대해 공부하고 해당 방법으로도 풀어봐야겠다..!)
분할정복
가장 직관적이면서도 쉬운 방법인 구간 내 가운데를 기준으로 분할 하는 방식으로 해결했다.
가운데를 기준으로 분할하여 풀이 할 때 아래 4가지 과정만 유의하여 작성하면 된다. (구간 범위 [lo : hi])
-
가운데 위치를 구한다. ( mid = (lo + hi) / 2 )
-
가운데 위치를 기준으로 분할하여 왼쪽 구간의 넓이([lo : mid])와 오른쪽 구간의 넓이([mid : hi])를 구한다.
-
왼쪽과 오른쪽 중 큰 넓이를 변수에 저장한다.
-
변수에 저장된 넓이와 두 구간을 합친 구간([lo : hi])의 가장 큰 넓이를 구해 두 개 중 가장 큰 넓이를 반환한다.
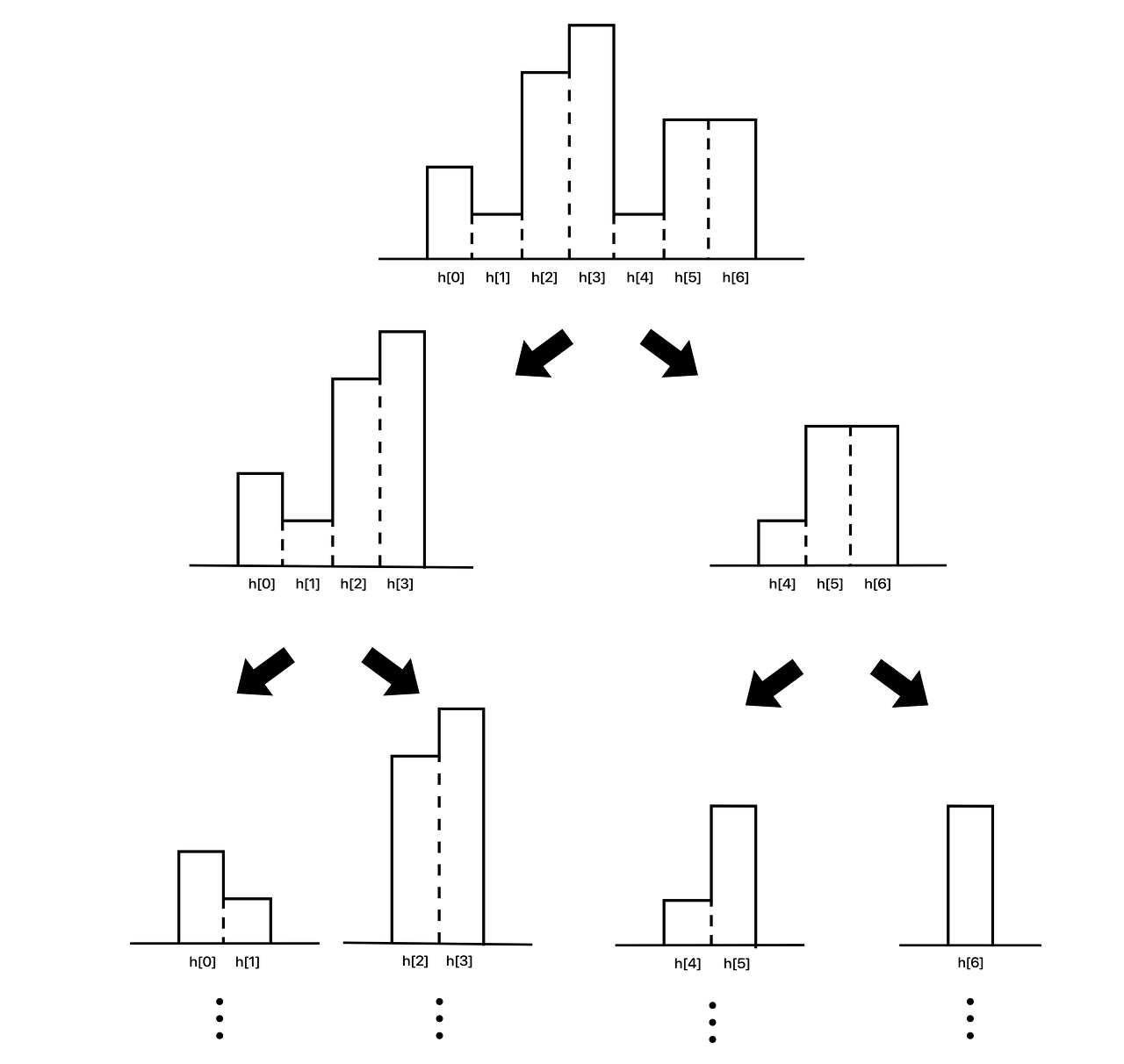
막대의 넓이가 1일 때까지 재귀과정을 거친다.
public static long getArea(int lo, int hi){
//막대의 폭이 1일 경우 높이가 넓이가 되기에 바로 반환
if(lo==hi){
return histogram[lo];
}
//1번
int mid = (lo+hi)/2;
//2번
long leftArea = getArea(lo,mid);
long rightArea = getArea(mid+1,hi);
//3번
long max = Math.max(leftArea,rightArea);
//4번
return max;
}4번을 해야하는 이유?
왼쪽 및 오른쪽으로 분할하여 얻어진 최대 넓이가 전체 구간(lo~hi) 내의 최대 넓이라는 보장이 없기 때문
그래서
mid를 기준으로 양쪽으로 뻗어나가면서 두 구간 사이의 겹친 넓이를 탐색해야 한다!
그러면 어떻게 중간 부분을 탐색해야할까?
일단 왼쪽과 오른쪽 중 어떤걸 고를까? -> 높이가 큰게 좋을것
이때 기존 높이와 새로운 높이 중 작은 것을 골라야 한다!
즉, 우리는 세 가지의 과정만 유의하면서 처리해주면 된다.
-
양쪽 다음 인덱스 중 높이가 큰 쪽으로 확장(padding)한다.
-
갱신되는 높이는 기존의 높이와 확장 한 막대의 높이 중 작은 것을 선택한다.
-
기존의 넓이와 확장한 넓이 중 큰 값으로 갱신한다.
다음의 과정을 그림으로 확인해보자
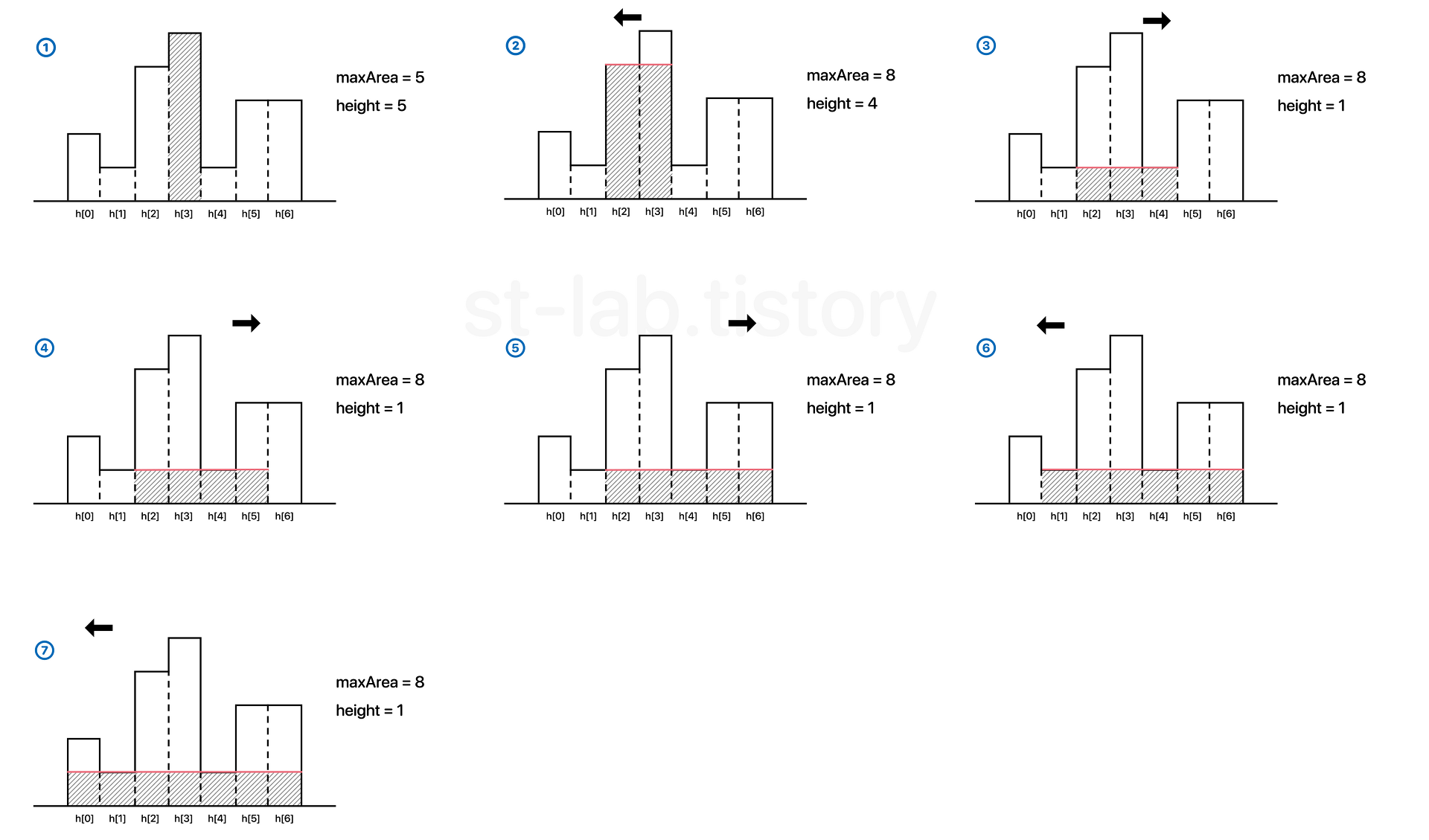
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static int[] histogram;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
StringBuilder sb = new StringBuilder();
while(true){
st = new StringTokenizer(br.readLine()," ");
int n = Integer.parseInt(st.nextToken());
if(n==0){
break;
}
histogram = new int[n];
for(int i=0;i<n;i++){
histogram[i] = Integer.parseInt(st.nextToken());
}
sb.append(getArea(0,n-1)).append('\n');
histogram = null;
}
System.out.println(sb);
}
public static long getArea(int lo, int hi){
//막대의 폭이 1일 경우 높이가 넓이가 되기에 바로 반환
if(lo==hi){
return histogram[lo];
}
//1번
int mid = (lo+hi)/2;
//2번
long leftArea = getArea(lo,mid);
long rightArea = getArea(mid+1,hi);
//3번
long max = Math.max(leftArea,rightArea);
//4번 - 양쪽 구간 중 큰 값과 중간 구간을 비교하여 더 큰 넓이로 갱신
max = Math.max(max,getMidArea(lo,hi,mid));
return max;
}
//중간 지점 영역의 넓이를 구하는 메소드
public static long getMidArea(int lo, int hi, int mid){
int toLeft = mid; //중간 지점으로부터 왼쪽으로 갈 변수
int toRight = mid; //중간 지점으로부터 오른쪽으로 갈 변수
long height = histogram[mid]; //높이
//초기 넓이는 구간폭이 1이기에 높이가 넓이
long maxArea = height;
//양 끝 범위를 벗어나기 전까지 반복
while(lo<toLeft && hi > toRight){
/*
양쪽 다음칸의 높이 중 높은거 선택,
단 갱신되는 height는 기존 height보다 작거나 같아야 함.
*/
if(histogram[toLeft-1] < histogram[toRight+1]){
toRight++;
height = Math.min(height,histogram[toRight]);
}
else{
toLeft--;
height = Math.min(height,histogram[toLeft]);
}
//최대 넓이 갱신
maxArea = Math.max(maxArea,height*(toRight - toLeft + 1));
}
//오른쪽 구간을 끝까지 탐색 못했다면 마저 탐색
while(toRight < hi){
toRight++;
height = Math.min(height,histogram[toRight]);
maxArea = Math.max(maxArea,height*(toRight - toLeft + 1));
}
//왼쪽 구간을 끝까지 탐색 못했다면 마저 탐색
while(toLeft > lo){
toLeft--;
height = Math.min(height,histogram[toLeft]);
maxArea = Math.max(maxArea,height*(toRight - toLeft + 1));
}
return maxArea;
}
}한줄평..
이번에 처음 플레티넘 문제를 풀어봤는데, 풀었다라는 말이 무색하게 찾아보고 이해하기도 벅찼다.. 하지만 막상 문제를 구현해보면 코드 자체는 그렇게 어렵지 않았다.
문제를 처음 접했을 때, 어떤 알고리즘을 사용해 어떻게 구현할지 그런 능력이 중요함을 느꼈다.
어려운 문제도 내 손으로 해결할 수 있을때까지 백준 문제를 풀어볼 것이다!