[백준] 1629번 : 곱셈

분할정복

---

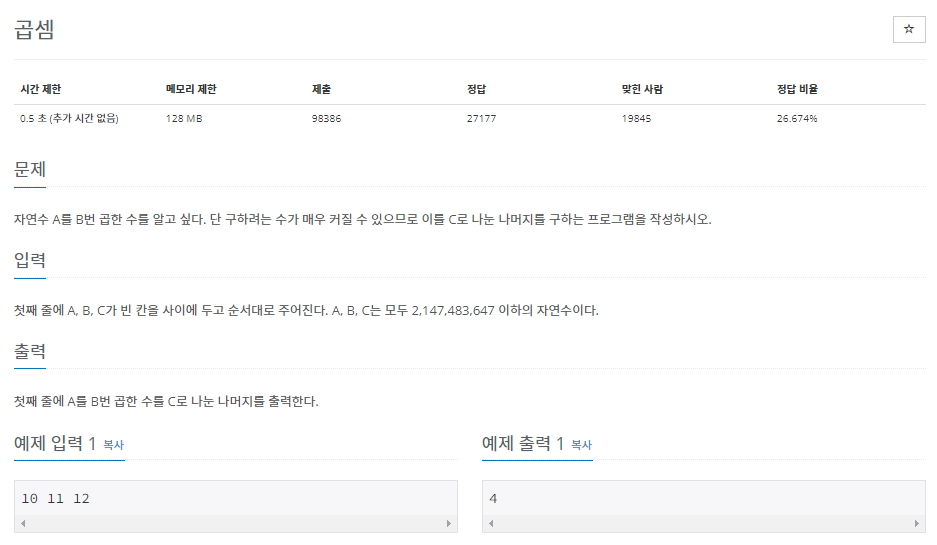
풀이 방법

다소 간단한 문제로 보이지만, 2,147,483,647 범위에 시간 제한은 0.5초가 주어졌기 때문에 그냥 제곱해버리면 시간 초과가 날것이기에 다른 방법을 찾아야 한다.

이번 문제는 '지수 법칙'과 '모듈러 성질'을 알고 있다면 쉽게 해결할 수 있는 문제이다.

나는 모듈러 성질에 대해 정확히 알고있지 않아서 풀이를 보고 해결한 문제였다...
모듈러 연산이란 나머지와 관련된 연산식이라고 생각하면 될 것 같다.

먼저 지수법칙
$a^{n+m}=a^n+a^m$

그리고 필요한 모듈러 성질
$(a\times b)\; mod\; C =(a\; mod\; C \times b\; mode\; C)\; mod\; C$

이것을 코드에서 사용하는 연산자를 사용해서 표현해보면

(a*b) % C = (a%C * b%C) % C

여기서 해당 모듈러 식에 대한 증명은 하지 않겠다..

예제풀이

예제에 보면 A가 밑, B가 지수, C는 결과값에 나눌 값이다.
먼저 거듭제곱을 어떻게 할지 고민해보자면

지수를 반으로 나누는 것이다.
다음 수식을 통해 이해해보자

먼저 지수가 짝수인 경우
$a^8 = a^4 * a^4$
$\,\,\,\,\,\,\,=(a^2*a^2)*(a^2*a^2)$
$\,\,\,\,\,\,\,=((a^1*a^1)*(a^1*a^1))*((a^1*a^1)*(a^1*a^1))$

다음은 지수가 홀수인 경우
$a^9 = a^4 * a^4 * a$
$\,\,\,\,\,\,\,=(a^2*a^2)*(a^2*a^2) * a$
$\,\,\,\,\,\,\,=((a^1*a^1)*(a^1*a^1))*((a^1*a^1)*(a^1*a^1)) * a$

예제의 A=10, B=11을 위와 같이 적용해보면 다음 그림과 같다.

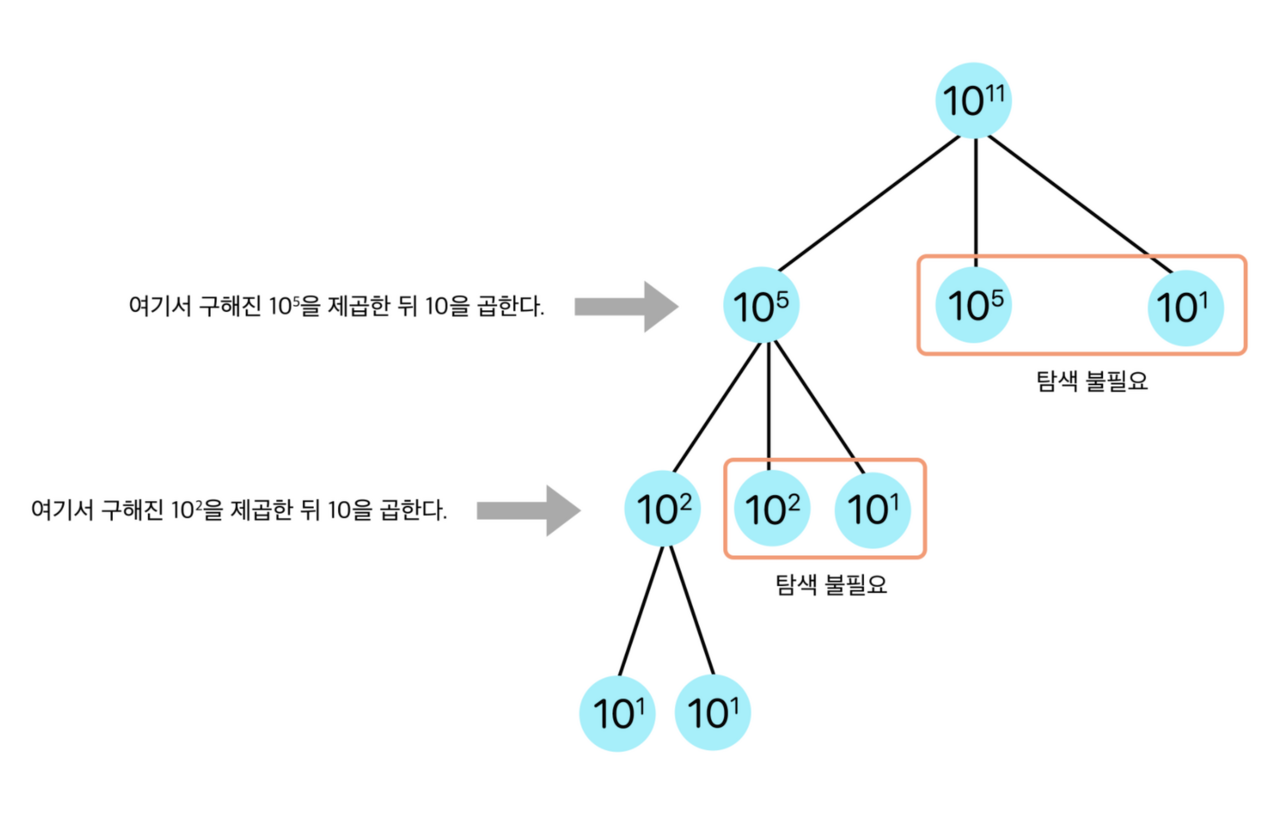
다음을 코드로 구현해보면

    public static long pow(long a, long exp){
        //지수가 1이라면 A^1 그대로 반환
        if(exp==1){
            return a;
        }

        //지수의 절반에 해당하는 값 구함
        long temp = pow(a,exp/2);

        //만약 지수가 홀수라면
        if(exp%2==1){
            //a를 한번 더 곱함
            return temp*temp*a;
        }
        //그 외는 짝수이기에 구했던 값을 한 번 더 곱해서 반환
        return temp*temp;
    }

다음으로는 모듈러 연산을 구현해보겠다.

그냥 리턴되는 값에 나머지 값만 다음처럼 붙이면

long pow(long A, long exponent) {
	if(exponent == 1) {
		return A % C;
	}
 
	/*
	 * 중략
	 */
 	if(exponent % 2 == 1) {
		return temp * temp * A % C;
	}
    
	return temp * temp % C;
}

이렇게 하면 틀린다.
왜?? 다음부분을 보자

if(exponent % 2 == 1) {
	return temp * temp * A % C;
}

문제에서 주어지는 각 최댓값은 int형의 max값이다. 즉, $2,147,483,647 (2^{31}-1)$을 입력받을 수 있다는 뜻이다. 대략 $2*10^9$ 정도 된다.

long형의 경우 $9,223,372,036,854,775,807 (2^{63}-1)$ 이고 대략 $9*10^{18}$ 정도 된다.

예로들어 temp가 2,147,483,647 라면 어떻게 할 것인가.
$temp \; *\; temp$는 long형 안에서 오버플로우 없이(long 타입 범위 안) 가능하다.
$(2^{31}-1)(2^{31}-1)<2^{63}-1$ 이 식을 만족하기 때문에
$temp \; * \; temp\;\%\;C$는 가능하다는 뜻이다.

모듈러 공식이 필요한 이유가 이 때문이다.
$(a\times b)\; mod\; C =(a\; mod\; C \times b\; mode\; C)\; mod\; C$
위 식을 다시 보자.

여기서 $temp \; *\; temp$ 는 long 형 범위를 넘어가지 않으니 a라고 보고, b를 A라고 생각하면 다음과 같이 변형할 수 있다.

// (a * b) % C = ((a % C)*(b % C)) % C
(temp * temp * A) % C = ((temp * temp % C) * (A % C)) % C
					  = (((temp * temp % C) % C) * (A % C)) % C 	// (temp * temp % C) = (temp * temp % C) % C
					  = ((temp * temp % C) * A) % C

즉, 이 부분만 고려하여 다음과 같이 리턴 값에 모듈러 연산을 해주면 된다.

---

코드

import java.io.*;
import java.util.*;

class Main {
    static long c;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine(), " ");
        long a = Long.parseLong(st.nextToken());
        long b = Long.parseLong(st.nextToken());
        c = Long.parseLong(st.nextToken());
        System.out.println(pow(a,b));
    }
    public static long pow(long a, long exp){
        if(exp==1){
            return a%c;
        }

        long temp = pow(a,exp/2);

        if(exp%2==1){
        	//(temp * temp * a) % C -> ((temp * temp % c) * (a % c)) % c
            return ((temp*temp%c) * a) %c;
        }
        return temp*temp%c;
    }
}

---

출처

https://st-lab.tistory.com/237
자주 참고하는 사이트입니다! 항상 감사합니다!!