[백준] 2110번 : 공유기 설치

공유기 설치

---

해결 방법

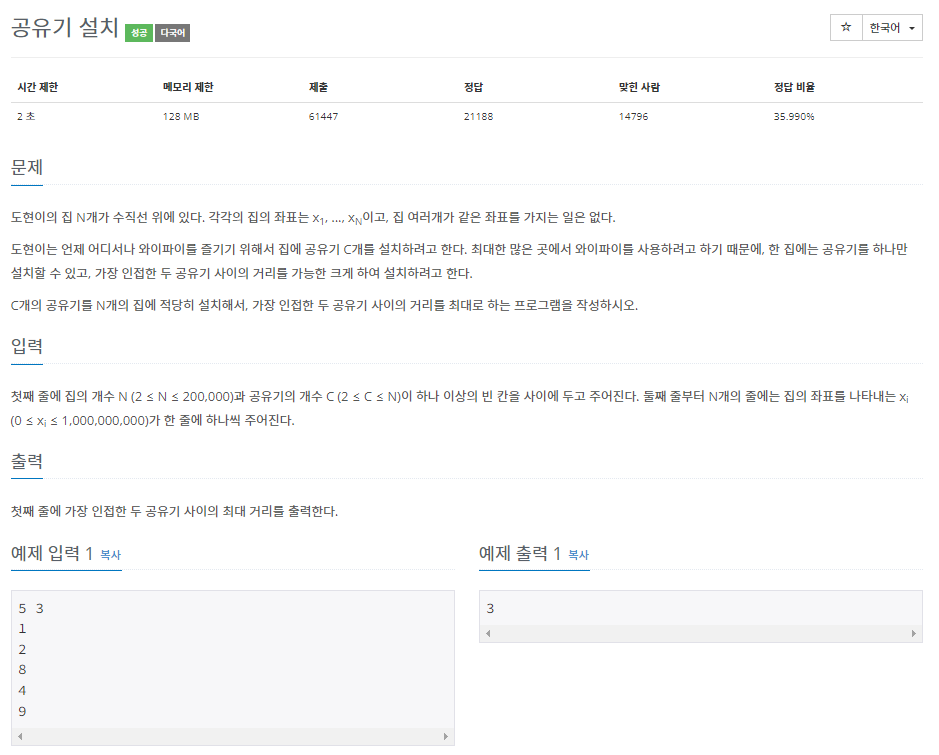
집의 좌표의 최대 크기가 10억개 이므로 완전 탐색으로 풀기엔 시간이 부족하다.
-> 이분탐색을 사용하자

이 문제는 코드가 진행되는 과정을 이해해야 해결 가능한 문제였다.

가장 인접한 두 공유기의 최대 거리를 구하는 문제인데

예제 풀이

max를 공유기를 설치할 수 있는 집 사이의 최대 거리로 잡고, min을 최소 거리로 잡는다.

만약 집 좌표가 {1,2,4,8,9}라면 max 값은 8 , min 값은 1이라는 것을 구할 수 있다.
그럼 mid 값이 4가되면,
{1,8}로 결과는 2가 나온다.
왜? -> 첫 번째 좌표에서 출발해 인접한 좌표 순으로 비교하면서 되는 것만 count해주면 되니까..

그러면 이 예제에서 원하는 결과(3)와 다르기 때문에
결과 값이 원하는 결과보다 작다면?? -> max 값을 줄임.

• 그러면 mid 값도 줄어드니까 더 좁은 간격으로 계산하기 때문에
  
  

결과 값이 원하는 결과보다 크거나 같다면??
-> 현재 mid(간격)를 저장하고, min 값을 늘린다.

• 현재 값을 저장해놓고, 더 큰 간격에서도 가능한지 확인한다. => 최대 값 구하기

예제를 마저 풀이해보면
결과가 2가 나왔기 때문에 max 값을 mid-1로 줄인다.
그러면 max = 3 , min = 1로 계산된다. mid = 2
{1,4,8}로 원하는 결과 3과 같기 때문에, 값을 저장하고 간격을 늘려본다.

max = 3 , min = 3 , mid = 3
{1,4,8} 그래도 원하는 결과가 나오기에 최대 값인 3이 정답이 된다.

---

코드

import java.io.*;
import java.util.*;

class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine(), " ");
        int n = Integer.parseInt(st.nextToken());
        int c = Integer.parseInt(st.nextToken());
        long[] router = new long[n];
        for(int i=0;i<n;i++){
            router[i] = Integer.parseInt(br.readLine());
        }

        Arrays.sort(router);
        System.out.println(binarySearch(
                c,1,router[n-1]-router[0],router));

    }
    public static long binarySearch(int num,long min, long max,long[] router){
        long result=0;
        while(min<=max){
            long mid = (min+max)/2;
            
            long count=1;
            int m=0;
            for (int i = 0; i < router.length; i++) {
                if (router[i] - router[m] >= mid) { //공유기 설치 가능 여부
                    count++;
                    m=i; //가능하면 그 위치가 시작지점이 됨.
                }
            }
            if(count<num){
                max = mid-1;
            }
            else{
                result = mid;
                min = mid + 1;
            }

        }
        return result;
    }
}