[백준] 5639번 : 이진 검색 트리

이진 검색 트리

---

풀이 방법

전에 풀어봤던 트리 순회의 변형 문제 같은 느낌이였다.
'트리 순회' 문제에서 트리 구조를 확실히 이해하고 넘어왔기 때문에 이번 문제는 상당히 쉬웠다.

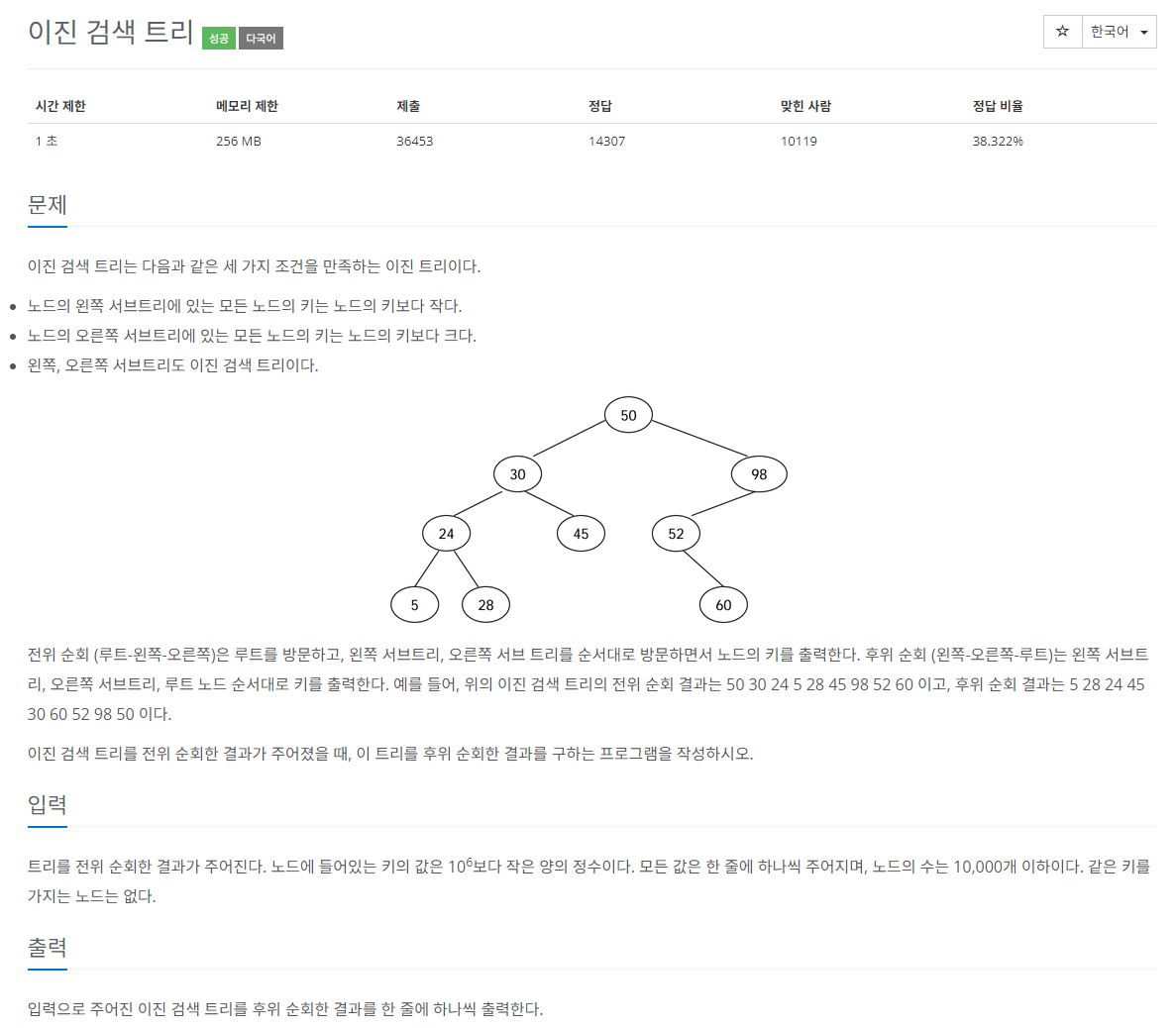
• 노드의 왼쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 작다.
• 노드의 오른쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 크다.
• 왼쪽, 오른쪽 서브트리도 이진 검색 트리이다.

해당 문제 조건에 맞춰서 변형시켜주기만 한다면 해결 가능하다.

느낀 점

이번 입력은 끝이 주어지지 않아서 while문을 돌려서 마지막 문자열을 검사했다.
str.equals("") 이렇게 마지막에 빈 문자열이 들어오면 종료되게 만들었는데, 이렇게만 돌리니까 백준 검사에서 런타임 에러 (NullPointer)가 나버렸다..
해결 방법으로는 str == null || str.equals("") 이런 식으로 EOF 처리를 해줘야 한다고 한다.
물론 str==null만 사용하는 것도 가능하다

---

소스 코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

class Node {
    int value;
    Node left;
    Node right;
    public Node(int value) {
        this.value = value;
    }
}

class Tree {
    Node root;
    public void InsertNode(int value){
        if(root == null){
            root = new Node(value);
        } else{
            searchNode(root, value);
        }
    }
    private void searchNode(Node root, int value) {
        if(value < root.value ){
            if(root.left == null) {
                root.left = new Node(value);
            }
            else{
                searchNode(root.left,value);
            }
        }
        else if(value > root.value){
            if(root.right == null){
                root.right = new Node(value);
            }
            else{
                searchNode(root.right,value);
            }
        }
    }
    public void postOrder(Node node) {
        if(node != null){
            postOrder(node.left);
            postOrder(node.right);
            System.out.println(node.value);
        }
    }
}

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        Tree tree = new Tree();

        while(true){
            String str = br.readLine();
            if(str == null || str.equals("")) break;
            int n = Integer.parseInt(str);
            tree.InsertNode(n);
        }

        tree.postOrder(tree.root);
    }
}