[백준] 9465번 : 스티커

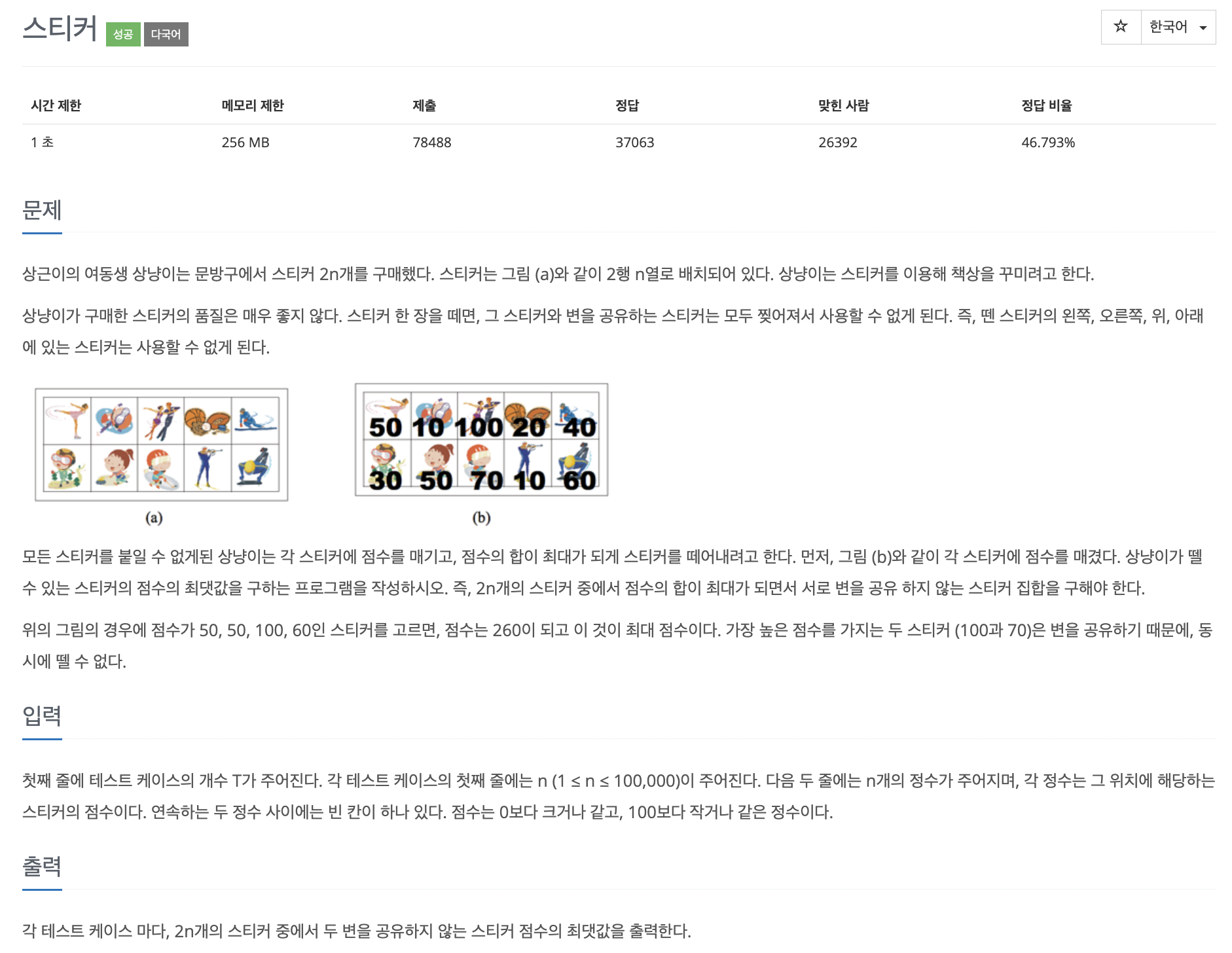
오랜만에 DP 문제를 풀어봤다.
확실히 DP 문제는 그림을 그려서 각 자리에서의 최대값을 어떻게 구할지 생각해보면 답이 눈에 보이는 것 같다.

여기서는 2열짜리 2차원배열로 주어지는데, 각 자리의 스티커를 뗐을 때 최대값을 구하면 된다.

계산을 쉽게 하기 위해서 0번째 자리([0,0], [1,0])는 0으로 초기화해두고,
[0,1], [1,1] 열에서의 최대값은 항상 자기자신이기에 설정해두고 시작한다.

2번째 자리 부터는 그 자리의 스티커를 떼면 이전 값들의 최대값과 비교를해서 각 자리에서 최대값을 업데이트 해줘야 한다.

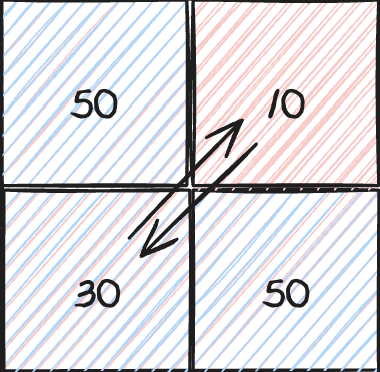
처음에는 이런식으로 10에서 자리를 떼면 앞에 자리 대각선만 계산해주면 될 줄 알았는데,

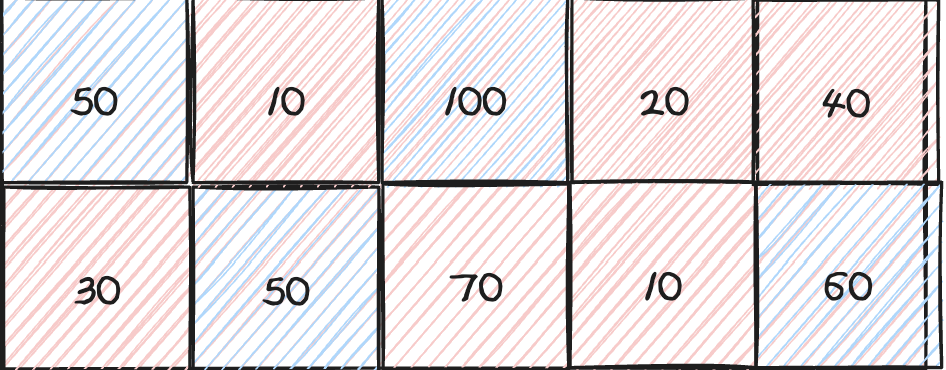
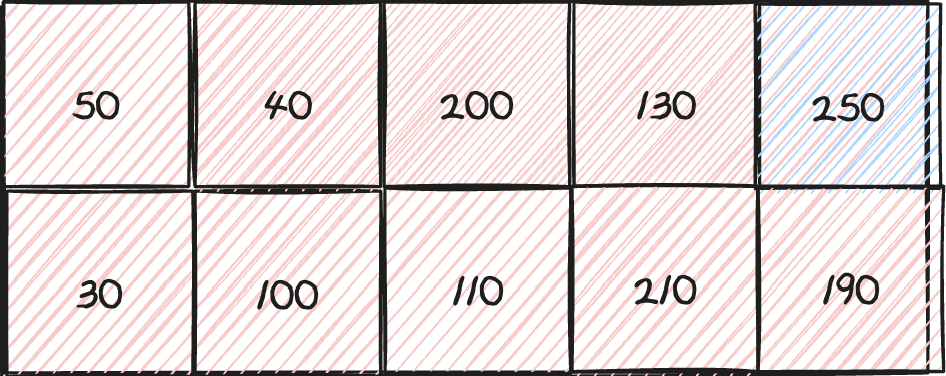
이런식으로 50,50,100,60 으로 마지막에 60을 골라야 하는데, 10+40 을 선택하는 문제가 발생했다.

그래서 100을 기준으로 생각해보면

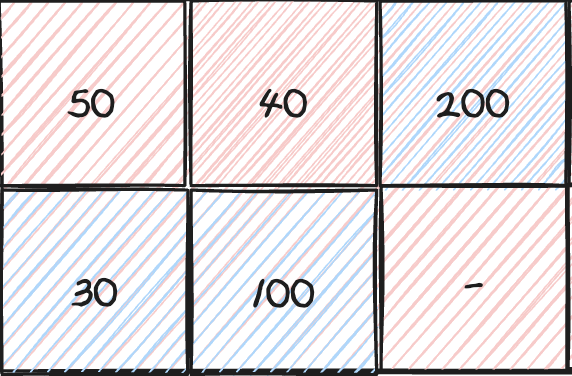
이처럼 [0,3] 자리에서는 [1,2],[1,1] 자리를 비교해서 최대값을 선택하는 방법을 사용하면 각 자리에서의 최대값을 제대로 구할 수 있다.

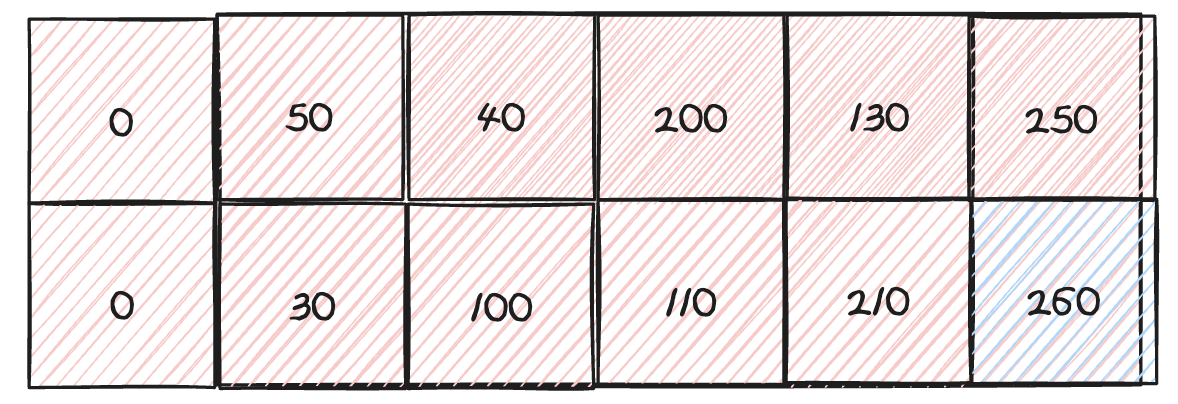
결과적으론 다음처럼 dp 배열이 이루어짐을 알 수 있다. 마지막에 [0,N],[1,N] 둘 중 최대값을 구해준다면 정답을 찾아낼 수 있다.

import java.io.*;
import java.util.*;

/**
 * 1 ≤ N ≤ 100,000
 * 시간 제한 1초
 * 메모리 제한 256 MB
 * ---
 *
 */

public class Main {
    public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    public static StringBuilder sb = new StringBuilder();
    public static StringTokenizer st;
    public static int T;

    public static void main(String[] args) throws IOException {
        T = Integer.parseInt(br.readLine());

        for (int i=0; i<T; i++) {
            int N = Integer.parseInt(br.readLine());
            int[][] arr = new int[2][N+1];
            int[][] dp = new int[2][N+1];
            for (int j=0; j<2; j++) {
                st = new StringTokenizer(br.readLine(), " ");
                for (int k=1; k<=N; k++) {
                    arr[j][k] = Integer.parseInt(st.nextToken());
                }
            }

            dp[0][1] = arr[0][1];
            dp[1][1] = arr[1][1];
            for (int k=2; k<=N; k++) {
                dp[0][k] = Math.max(dp[1][k-1], dp[1][k-2]) + arr[0][k];
                dp[1][k] = Math.max(dp[0][k-1], dp[0][k-2]) + arr[1][k];
            }
            sb.append(Math.max(dp[1][N], dp[0][N])).append("\n");
        }
        System.out.print(sb);
    }
}