[자료구조] 그래프(Graph)

그래프(Graph)의 개념

단순히 노드(N, node)와 그 노드를 연결하는 간선(E, edge)을 하나로 모아 놓은 자료 구조

---

그래프 용어

• 노드(node) : 정점(vertice)라고도 불리며, 일반적으로 노드에는 데이터가 저장됨
• 간선(edge) : 링크, arcs라고도 불리며, 노드간의 관계를 나타냄
• 인접 정점(adjacent vertex) : 간선에 의해 연결된 정점. 위 그림에서 노드A와 B는 인접 정점이라고 할 수 있다
• 단순 경로(simple-path) : 경로 중 반복되는 정점이 없는것, 같은 간선을 자나가지 않는 경로
• 차수(degree) : 무방향 그래프에서 하나의 정점에 인접한 정점의 수. 위 그래프에서 A의 차수는 3이다.
• 진출차수(out-degree)/진입차수(in-degree) : 방향그래프에서 사용되는 용어
  • 진출 차수 : 한 노드에서 외부로 향하는 간선의 수,
  • 진입차수 : 외부 노드에서 들어오는 간선의 수
• 사이클(cycle): 단순 경로의 출발지와 목적지가 같은 경우

---

그래프 종류

• 무방향 그래프(Undirected Graph)
  

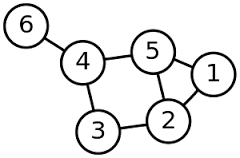
  무방향 그래프는 두 정점을 연결하는 간선에 방향이 없는 그래프이다.

• 방향 그래프(Directed Graph)
  

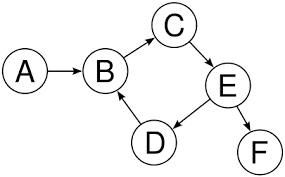
  방향 그래프는 두 정점을 연결하는 간선에 방향이 존재하는 그래프이다.
  간선의 방향으로만 이동할 수 있다.

• 가중치 그래프(Weighted Graph)
  

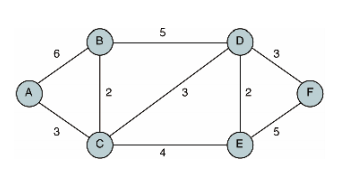
  가중치 그래프는 간선에 가중치(비용)가 할당된 그래프로, 두 정점을 이동할 때 비용이 드는 그래프이다.

• 연결 그래프(Connected Graph)
  

무방향 그래프에 있는 모든 정점 쌍에 대해서 항상 경로가 존재하는 그래프
대표적인 예) 트리

• 비연결 그래프(Disconnected Graph)
  

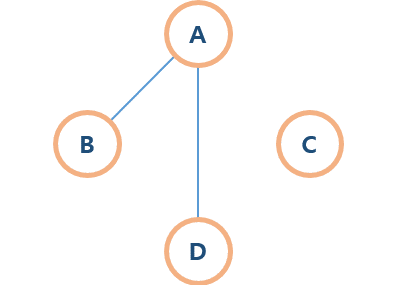
무방향 그래프에서 특정 정점 사이에 경로가 존재하지 않는 그래프
즉, 노드들 중 간선에 의해 연결되어 있지 않은 그래프이다.

• 완전 그래프(Complete graph)
  

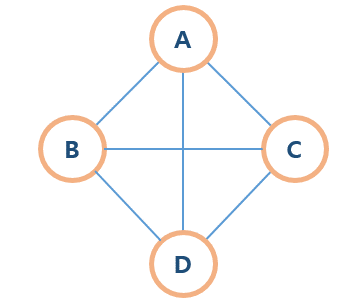
  그래프의 모든 정점이 서로 연결되어 있는 그래프이다. (인접 연결)

• 신장트리(Spanning Tree)
  

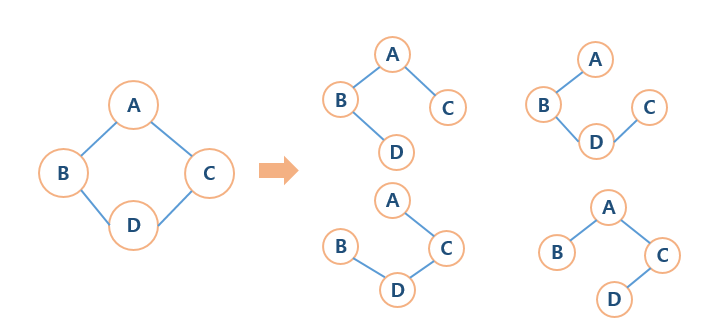
  원래 그래프의 모든 노드가 연결되어 있으면서, 트리의 속성을 만족하는 그래프
  
  트리의 속성을 만족하기 때문에 사이클이 존재하면 안된다.

• 최소 신장트리(Minimum Spanning Tree)
  

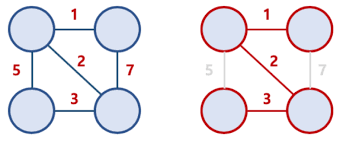
  신장트리(Spanning Tree)중 간선의 가중치 합이 최소인 신장 트리

---

그래프의 구현

그래프는 인접행렬 또는 인접리스트로 표현할 수 있다.

장/단점	인접 행렬	인접 리스트
시간 복잡도	O(N^2) 정점 N * N만큼 필요	O(N) N : 간선의 개수
두 정점의 연결 여부	graph[x][y] 의 값으로 한번에 확인	graph 의 원소에서 y가 나올때까지 탐색
인접 노드 파악 여부	N * N만큼 반복문을 돌아 확인한다.	각 리스트에 담겨있는 원소를 확인한다.

즉 둘 다 각각의 장단점을 가지고 있다.
간선이 많은 그래프 -> 인접행렬을 통해 빠르게 연결 여부 확인
간선이 적은 그래프 -> 인접리스트를 통해 빠르게 인접 노드 확인

1. 인접 행렬을 통한 구현

public class Main {
    public static void main(String[] args) throws IOException {
        int[][] edges = new int[][] {
                {1, 2}, {2, 3}, {3, 4}, {4, 5}
        };//

        int n = 5; //정점의 개수

        int[][] matrix = new int[n + 1][n + 1];

        for(int[] edge : edges) { //양방향 그래프
            matrix[edge[0]][edge[1]] = 1;
            matrix[edge[1]][edge[0]] = 1;
        }

        //출력
        for(int i = 1 ; i <= n ; i++) {
            for(int j = 1 ; j <= n ; j++) {
                System.out.print(matrix[i][j]+" ");
            }
            System.out.println();
        }
    }
}

출력 결과
0 1 0 0 0 
1 0 1 0 0 
0 1 0 1 0 
0 0 1 0 1 
0 0 0 1 0 

2. 인접 리스트를 통한 구현

	public class Main {
    public static void main(String[] args) throws IOException {
        int[][] edges = new int[][] {
                {1, 2}, {2, 3}, {3, 4}, {4, 5}
        };//

        int n = 5; //정점의 개수

        ArrayList<ArrayList<Integer>> list = new ArrayList<>();

        for(int i = 0 ; i <= n ; i++) list.add(new ArrayList<>());

        for(int[] edge : edges) {
            list.get(edge[0]).add(edge[1]);
            list.get(edge[1]).add(edge[0]);
        }

        //출력
        for (int i = 1; i < list.size(); i++) {
            for(int j = 0 ; j < list.get(i).size(); j++)
                System.out.print(list.get(i).get(j)+" ");
            System.out.println();
        }
    }
}

출력 결과
2 
1 3 
2 4 
3 5 
4