121. Best Time to Buy and Sell Stock

문제 링크: https://leetcode.com/problems/best-time-to-buy-and-sell-stock/?envType=study-plan-v2&envId=top-interview-150

주어진 조건

• prices: 해당 날짜의 특정 주식 가격을 나타내는 정수 배열

문제

• 수익을 극대화할 수 있도록 주식을 특정 날짜에 매수하고, 매도하려고 한다
• 이때 달성할 수 있는 최대 수익을 return 하자

---

나의 풀이

코테 문제는 처음부터 좋은 방법을 바로 떠올리기는 힘들다고 생각해, 일단 떠오르는 방법을 바로 시도해보았다.

완전탐색을 이용해 모든 경우를 하나씩 계산하는 방법이다. 이중 반복문 사용으로, 시간복잡도가 O(n^2)이고, 따라서 시간 초과 결과를 얻었다.

시도 1

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        answer = 0
        for i in range(len(prices)):
            for j in range(i+1, len(prices)):
                if prices[j] - prices[i] > answer:
                    answer = prices[j] - prices[i]
        

        return answer

위 시도를 한 번 최적화 해보자.

• prices의 요소 반복
• 최소 가격을 매번 업데이트
• 최대 수익 또한 매번 업데이트

for문을 한 번만 사용함으로써 시간복잡도 O(n)으로 감소

구현 코드

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        minPrice, profit = 100000, 0
        for price in prices:
            minPrice = min(minPrice, price)
            profit = max(profit, price - minPrice)
        return profit

---

다른 풀이 - Kadane

Kadane 알고리즘이란?

Maximum Subarray를 푸는 방법 중 하나의 알고리즘이다. (DP 중 하나)

핵심: 각각 최대 부분합은 이전 최대 부분합이 반영된 결과값

Kadane 알고리즘의 핵심을 따라, 최대 부분합은 이전 최대 부분합이라는 것을 이용했다

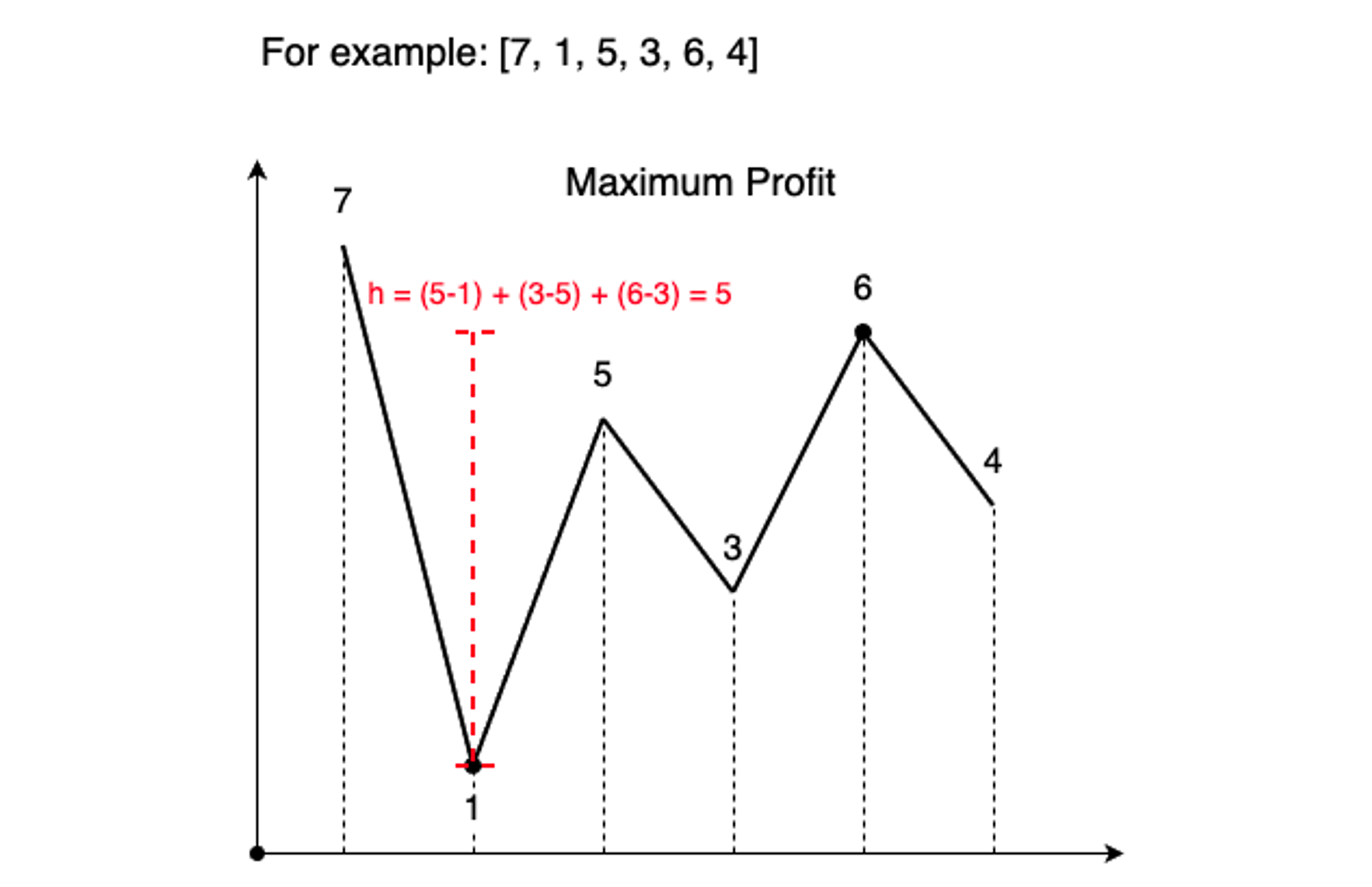
prices[n] - prices[n-4]

= (prices[n-3] - prices[n-4]) + (prices[n-2] - prices[n-3]) + (prices[n-1] - prices[n-2]) + (prices[n] - prices[n-1])

예를 들면, 위와 같은 방식으로 두 요소 값의 차이를 구할 수 있다.

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        n = len(prices)
        ans = 0
        curSum = 0
        for i in range(n-1):
            curSum += prices[i+1] - prices[i]
            if curSum < 0:
                curSum = 0
            ans = max(ans, curSum)
        return ans

위 코드 설명

Time: O(N)

Space: O(1)

• curSum에 이웃하는 두 요소 값의 차이를 차례대로 더해간다
  • 만약, 음수가 된다면 0 으로 초기화
• 현재 최대 수익과 curSum 비교하여 더 큰 값으로 업데이트

최대 부분합은 이전 최대 부분합이 반영된 결과값이라는 아이디어가 생각보다 코테에 많이 사용되는 것 같다.

완전 탐색으로 먼저 생각해보고 이후에 최적화하는 방향으로 사고과정을 갖는 것이 좀 더 아이디어를 떠올 릴때 유용하다고 느꼈다.