1823. Find the Winner of the Circular Game [Leet Code]

Problem

There are n friends that are playing a game. The friends are sitting in a circle and are numbered from 1 to n in clockwise order. More formally, moving clockwise from the ith friend brings you to the (i+1)th friend for 1 <= i < n, and moving clockwise from the nth friend brings you to the 1st friend.

The rules of the game are as follows:

1. Start at the 1st friend.
2. Count the next k friends in the clockwise direction including the friend you started at. The counting wraps around the circle and may count some friends more than once.
3. The last friend you counted leaves the circle and loses the game.
4. If there is still more than one friend in the circle, go back to step 2 starting from the friend immediately clockwise of the friend who just lost and repeat.
5. Else, the last friend in the circle wins the game.

Given the number of friends, n, and an integer k, return the winner of the game.

---

Examples

Example 1:

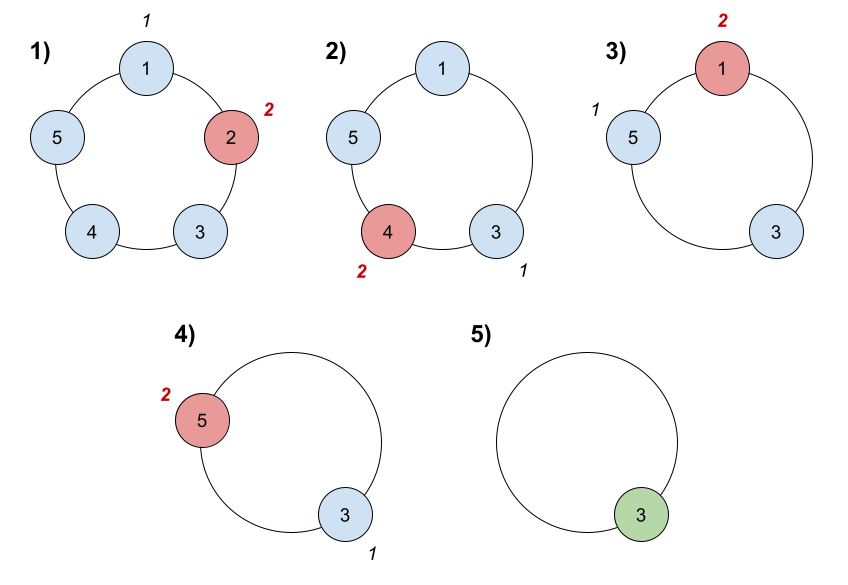
Input: n = 5, k = 2
Output: 3
Explanation: Here are the steps of the game:
1) Start at friend 1.
2) Count 2 friends clockwise, which are friends 1 and 2.
3) Friend 2 leaves the circle. Next start is friend 3.
4) Count 2 friends clockwise, which are friends 3 and 4.
5) Friend 4 leaves the circle. Next start is friend 5.
6) Count 2 friends clockwise, which are friends 5 and 1.
7) Friend 1 leaves the circle. Next start is friend 3.
8) Count 2 friends clockwise, which are friends 3 and 5.
9) Friend 5 leaves the circle. Only friend 3 is left, so they are the winner.

Example 2:

Input: n = 6, k = 5
Output: 1
Explanation: The friends leave in this order: 5, 4, 6, 2, 3. The winner is friend 1.

---

Constraints

1 <= k <= n <= 500

---

Code

Python

class Solution:
    def findTheWinner(self, n: int, k: int) -> int:
        lst = [i for i in range(1, n+1)]
        start = 0

        while len(lst) > 1:
            idx = (start + k -1) % len(lst) 
            lst.remove(lst[idx])

            start = idx % n

        return lst[0]
        

Swift

class Solution {
    func findTheWinner(_ n: Int, _ k: Int) -> Int {
        var start = 0
        var lst : [Int] = []
        var idx : Int
        for i in 1...n{
            lst.append(i)
        }

        while lst.count > 1 {
            idx = (start + k - 1) % lst.count
            lst.remove(at:idx)
            start = idx
        }
        return lst[0]
    }
}

list.remove()를 사용해서 제거 연산이 O(n) 시간 복잡도를 가진다. 따라서 전체 시간 복잡도는 O(n^2) 이며 공간 복잡도는 n개의 요소를 저장하기 위해 O(n)을 사용한다.