버블 정렬(Bubble Sort)

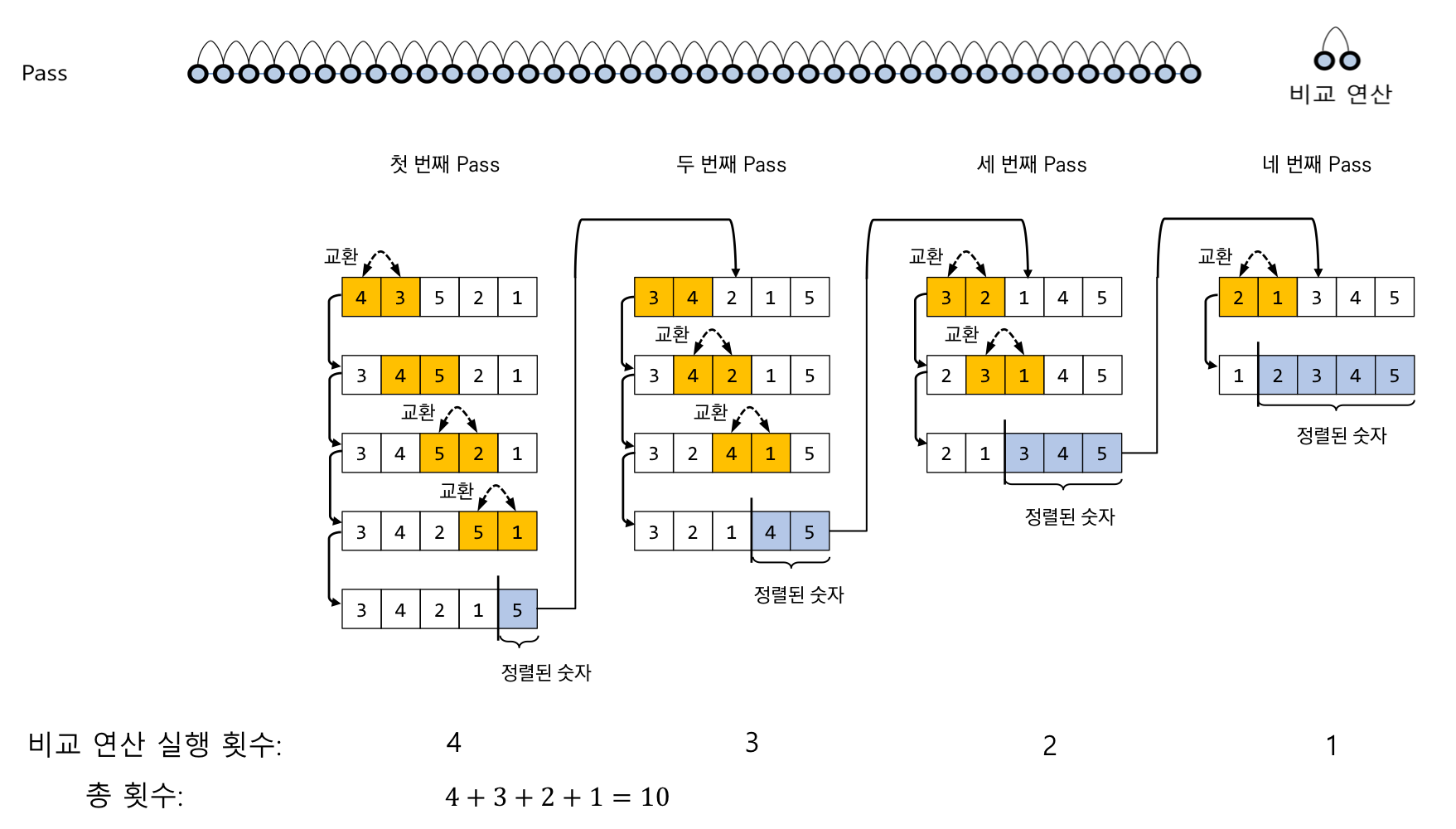
💡 버블 정렬(Bubble Sort) 이란?

인접한 두 숫자를 비교하여 두 수의 정렬 순서가 맞지 않는 경우에 교환(Swap) 하는 정렬

👉 Pass

• 맨 왼쪽 인접한 두 숫자부터 맨 오른쪽 끝 인접한 두 숫자를 비교할 때까지 연속적으로 인접한 두 숫자를 비교
• 비교한 두 숫자의 정렬 순서가 맞지 않을 경우에 교환(Swap)

👉 Pass의 결과

• 제일 큰 숫자가 맨 오른쪽 끝으로 이동
• 제일 큰 숫자는 더 이상 다음 Pass에 포함시킬 필요가 없음

👉 비교 횟수

• 입력 데이터의 개수를 n이라고 할 때, 한 Pass에서 n-1 번의 비교 실행
  
  
  

✔️ 버블 정렬 구현

void swap(int* a, int* b){
    int tmp = *a;
    *a = *b;
    *b= tmp;
}


void bubbleSort(int array[], int n){
    for(int pass=1; pass<n; pass++){
        for(int i=0; i<n-pass; i++){ // 정렬된 숫자 제외
            if(array[i] > array[i+1]){
                swap(array[i], array[i+1]);
            }
        }
    }
}

비교 횟수
👍 best case: n^2
👊 average case: n^2
👎 worst case: n^2

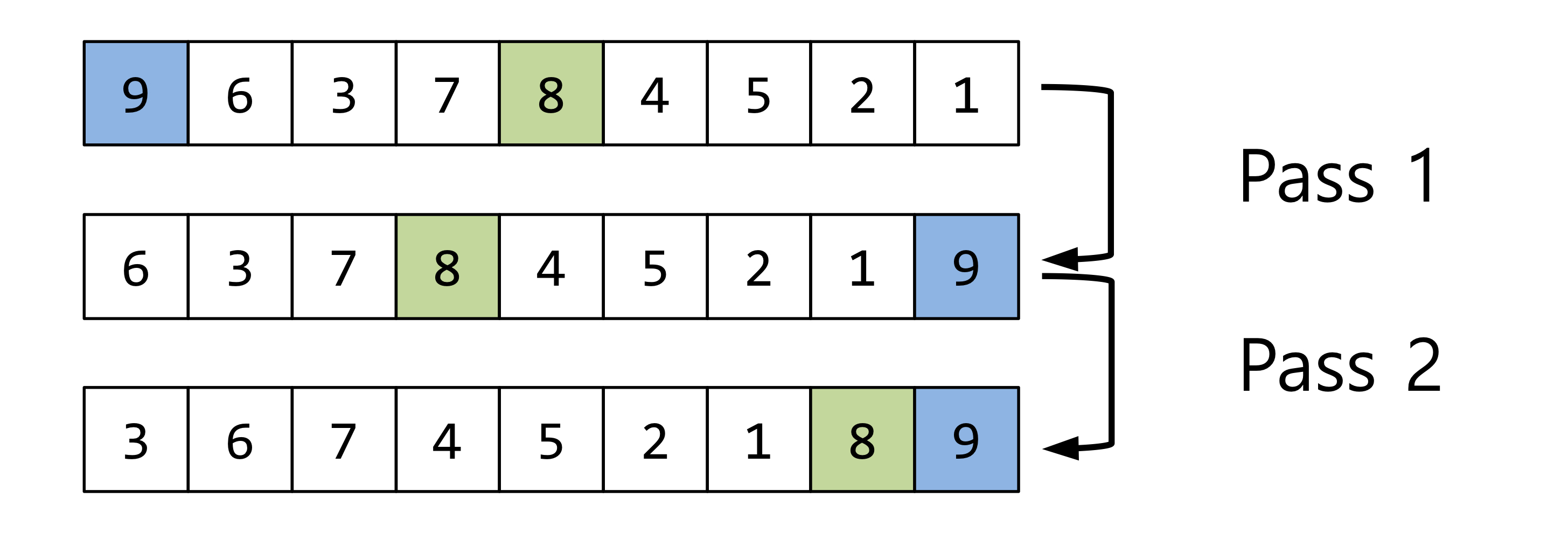
✔️ 토끼와 거북이 데이터

🐰 토끼 데이터(Rabbit Data)
왼쪽에서 오른쪽으로 빠르게(몇 번의 pass를 통하여) 제 위치로 이동하는 큰 데이터들

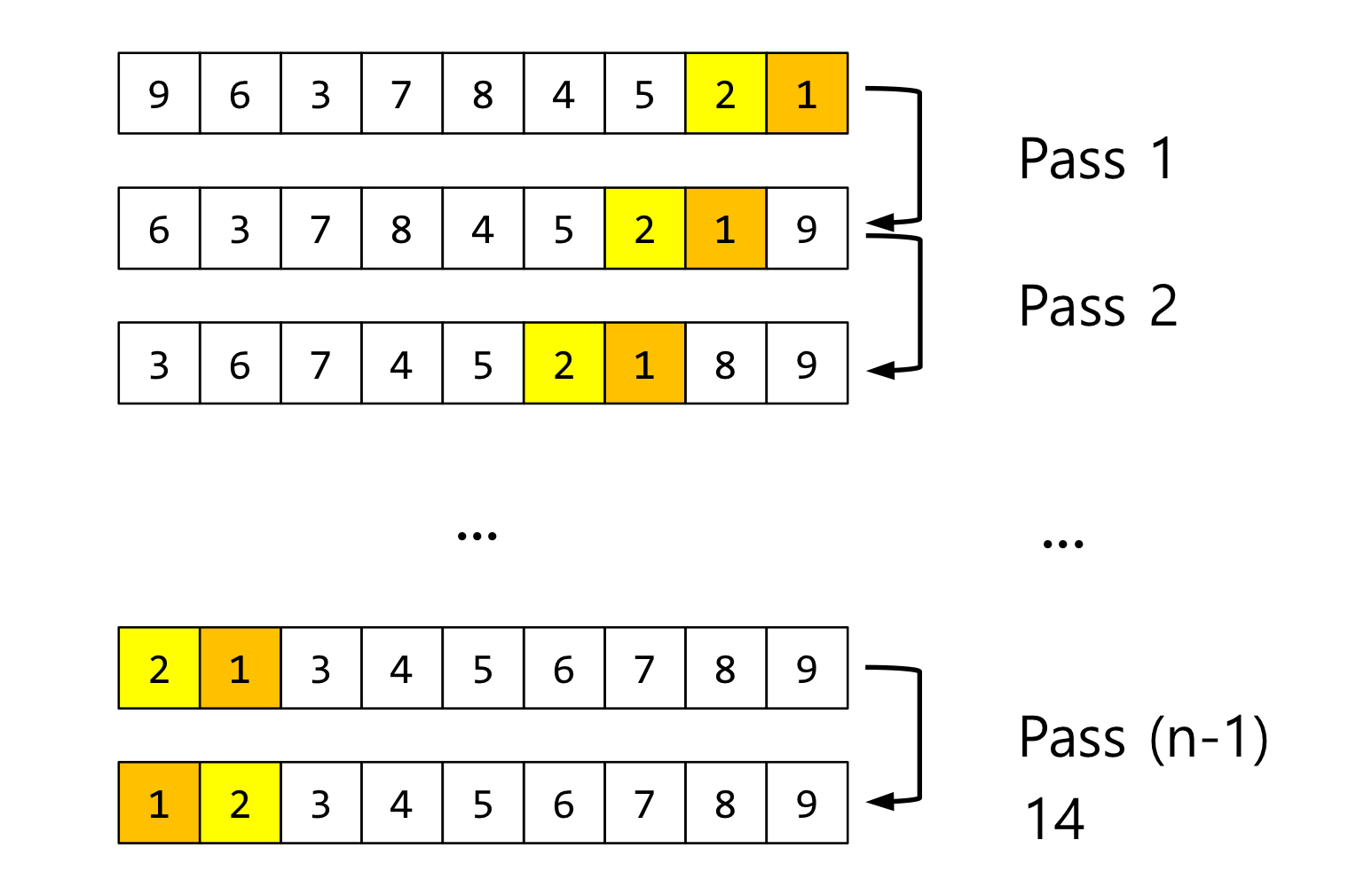
🐢 거북이 데이터(Turtle Data)
오른쪽에서 왼쪽으로 매우 느리게 제 위치로 이동하는 작은 데이터들

➕ 버블 정렬 개선 구현

개선 1

→ 해당 pass에서 데이터 교환했는지 판단. 교환하지 않았다면 모든 데이터가 정렬되어있으므로 종료함

void bubbleSortImproved1(int array[], int n){
    int swapped; 

    for(int pass=1; pass<n; pass++){
        swapped = 0;
        for(int i=0; i<n-pass; i++){
            if(array[i] > array[i+1]){
                swap(array[i], array[i+1]);
                swapped = 1;
            }
        }
        if(swapped == 0) break; // 이번 pass에서 swap하지 않았다면, 모든 데이터가 정렬되어 있음
    }
}

비교 횟수
👍 best case: n-1
→ 입력데이터가 오름차순으로 정렬되어 있는 경우
👎 worst case: n(n-1)/2
→ 입력데이터가 내림차순으로 정렬되어 있는 경우 등

개선2

→ 해당 pass에서 마지막으로 교환한 데이터의 위치 파악. 다음 pass에서는 이 위치 바로 앞까지만 실행함

void bubbleSortImproved2(int array[], int n){
    int lastSwappedPos = n-1;
    int swappedPos;

    for(int pass=1; pass<n; pass++){
        if(lastSwappedPos > 0){
            swappedPos = 0;
            for(int i=0; i<lastSwappedPos; i++){ // 마지막으로 교환한 index 바로 앞까지만 실행
                if(array[i] > array[i+1]){
                    swap(array[i], array[i+1]);
                    swappedPos = i;
                }
            }
            lastSwappedPos = swappedPos;
        }
    }
}

✔️ 시간복잡도 및 특징

시간 복잡도: O(n^2)

✔︎ Stable
✔︎ In-place