동적 계획법(DP)

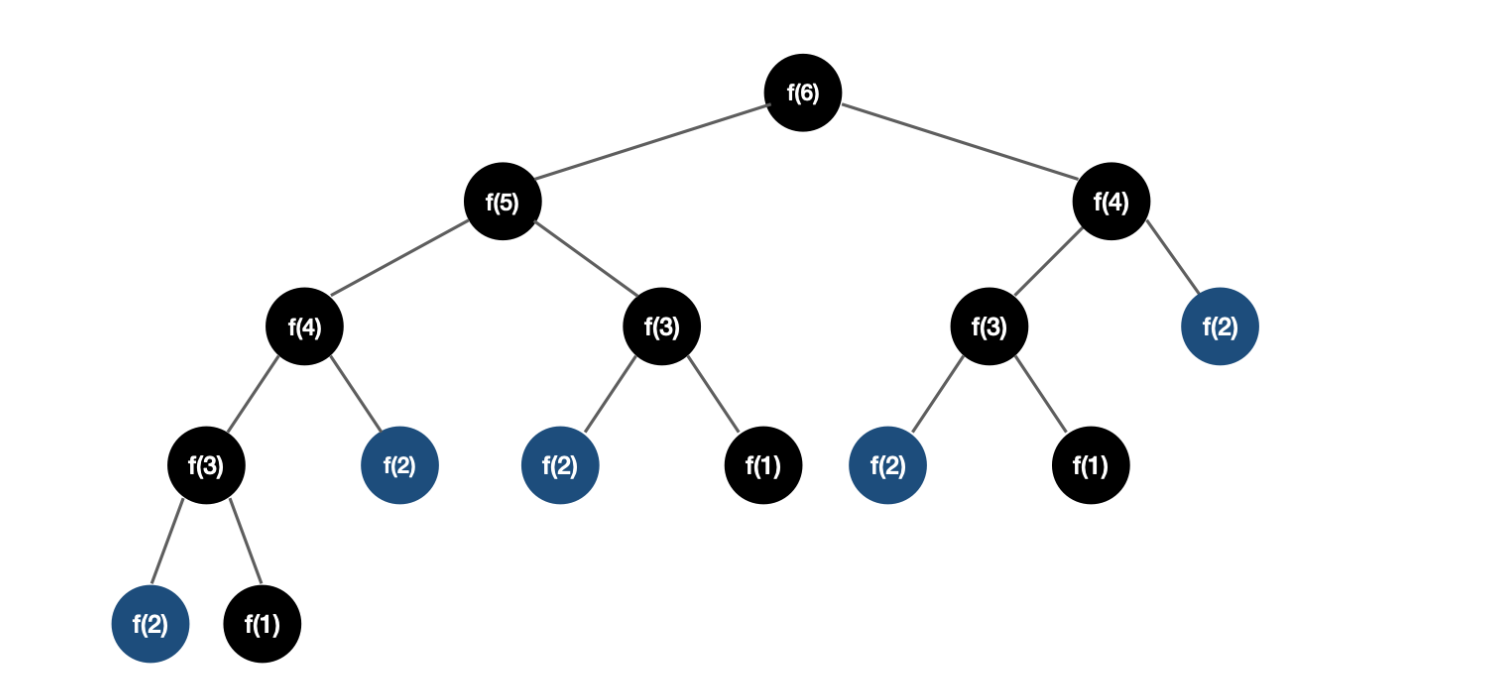
🔎 Dynamic Programming(동적 계획법)

• 하나의 큰 문제를 여러 개의 하위 문제로 나누어 풀고, 그것들을 결합하여 최종 목적에 도달하는 방식의 알고리즘이다.
• 처음 진행한 연산은 기록해 두고, 이미 진행했던 연산이라면 다시 연산하지 않고 기록되어 있는 값을 가져오는 메모이제이션 방식을 이용한다.
  

❓ 메모이제이션(Memoization)
    컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술이다.

• 일반적인 재귀(Recursion) 방식 또한 DP와 매우 유사하다.

  ❗️ Recursion과 DP 차이
  → 일반적인 Recursion을 사용할 때 동일한 작은 연산들이 여러 번 반복되어 비효율적인 계산이 될 수 있다.
  → 그러나, DP는 진행한 연산을 기록해두고 기록된 값을 가져오기 때문에 동일한 연산을 하지 않아 비효율적인 계산을 막을 수 있다.

       // **Recursion으로 작성한 피보나치**
       int fibo(int n){
       	if(n <= 2) return 1;
       	else return fibo(n-1) + fibo(n-2);
       }

        // **DP로 작성한 피보나치**
        int fiboData[100] = {0, }; // 모두 0으로 초기화
        
        int fibo(int n){
        	if(n <= 2) return 1;
        	if(fiboData[n] == 0){
        		fiboData[n] = fibo(n-1) + fibo(n-2);
        	}
        	return fiboData[n];
        }
        

  
  

🔎 사용 조건

☑️  동일한 작은 문제들이 반복하여 나타나는 경우에 사용 가능

☑️  부분 문제의 최적 결과 값을 사용해 전체 문제의 최적 결과를 낼 수 있는 경우에 사용 가능

🔎 구현 방법

👇 TOP-DOWN

문제 풀이가 위에서 아래로 진행되는 방식

int fiboData[100] = {0, }; // 모두 0으로 초기화

int fibo(int n){
	if(n <= 2) return 1;
	if(fiboData[n] == 0){
		fiboData[n] = fibo(n-1) + fibo(n-2);
	}
	return fiboData[n];
}

👆 BOTTOM-UP

문제 풀이가 아래에서 위로 진행되는 방식

int fiboData[100] = {0, };

int fibo3(int n){
    fiboData[0] = 0;
    fiboData[1] = 1;
    for (int i=2; i<=n; i++){
        fiboData[i] = fiboData[i-1] + fiboData[i-2];
    }
    return fiboData[n];
}

🆚 Greedy(탐욕법) 알고리즘

→ Greedy 알고리즘은 모든 해를 구하지 않고 그 순간마다 최적의 해를 찾는 방식의 알고리즘이다.
이는 모든 방법을 하나씩 검토하여 최적의 해를 찾아내는 DP 알고리즘과 대비된다.
→ Greedy 알고리즘은 닥치는 순간만을 고려하여 해를 구하기 때문에 도출된 값이 항상 최적의 해라고 할 수 없다.

→ 그러나, DP 알고리즘은 모든 방법 검토해보고 결과적으로 효율적인 값을 택한다.
⇒ DP 알고리즘은 Greedy 알고리즘에 비해 시간이 오래 걸리지만, 결과는 항상 최적의 해를 구할 수 있다.

References:

https://velog.io/@chelsea/1-동적-계획법Dynamic-Programming-DP

https://hongjw1938.tistory.com/47

https://ko.wikipedia.org/wiki/메모이제이션