- AR(Autoregression) 모형과 MA(Moving Average) 모형을 합친 모형
- 시계열 데이터의 정상성을 가정
정상성, 차분, 확률보행 모델
정상성(Stationary, 고정적)
-
정상성을 나타내는 시계열은 시계열의 특징이 해당 시계열이 관측된 시간에 무관함
-
또한 정상성을 나타내는 시계열은 평균, 분산, 공분산이 모두 시간에 따라 일정해야 한다.
- 추세와 계절성이 있는 시계열의 경우 서로 다른 시계열의 값에 영향을 주기 때문에 정상성을 나타내는 시계열이 아님
- 단, 백색잡음(white noise) 시계열의 경우 언제 관찰하는지에 상관이 없고, 시간에 따라 어떤 시점에서 보더라도 똑같이 보이므로 정상성을 나타내는 시계열이라 할 수 있다
- 주기성 행동을 가지는(추세나 계절성은 없는) 시계열은 주기가 고정된 길이를 가지고 있지 않아 시계열 관측 전 주기의 고점/저점 확인하기 어려워 정상성을 나타내는 시계열이라 할 수 있다
-
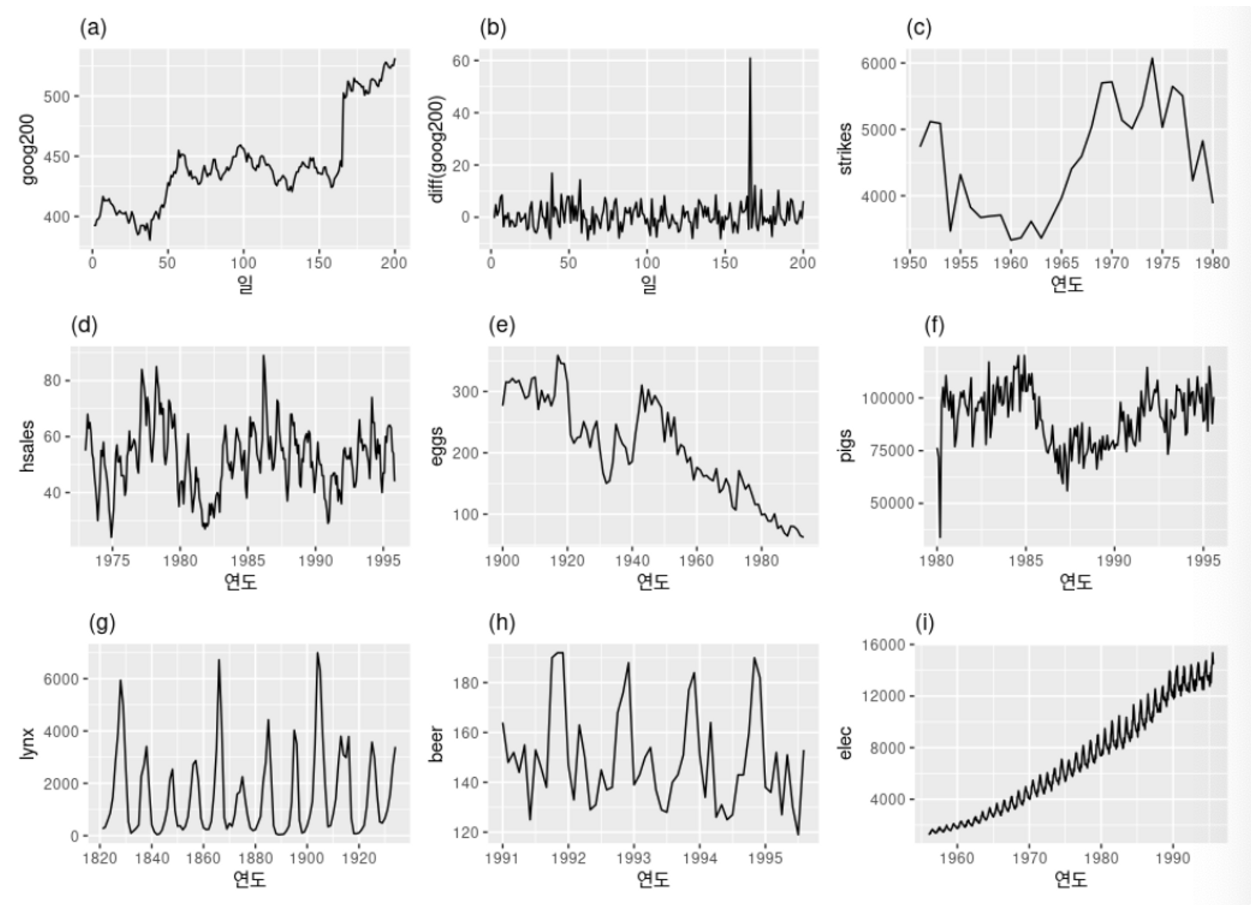
정상성 만족하는 데이터 구분
- (d), (h), (i) → 계절성이 보이므로 비정상 시계열
- (a), (c), (e), (f), (i) → 추세가 존재하고 수준이 변하므로 비정상 시계열
- (i) → 분산이 증가하므로 비정상 시계열
- (b), (g) → 정상시계열
- (g)의 경우 뚜렷한 주기(cycle)이 보여 비정상 시계열처럼 보일 수 있으나, 이러한 주기는 불규칙적(aperiodic)한 주기이다
- 불규칙적 주기의 경우 장기적으로 볼때 주기의 시작이나 끝을 예측할 수 없다
-
정상성을 나타내지 않는 데이터를 정상 시계열로 변환하는 방법
- 변동폭이 일정하지 않은 경우 → 로그 변환
- 추세, 계절성이 존재하는 경우 → 차분(differencing)
-
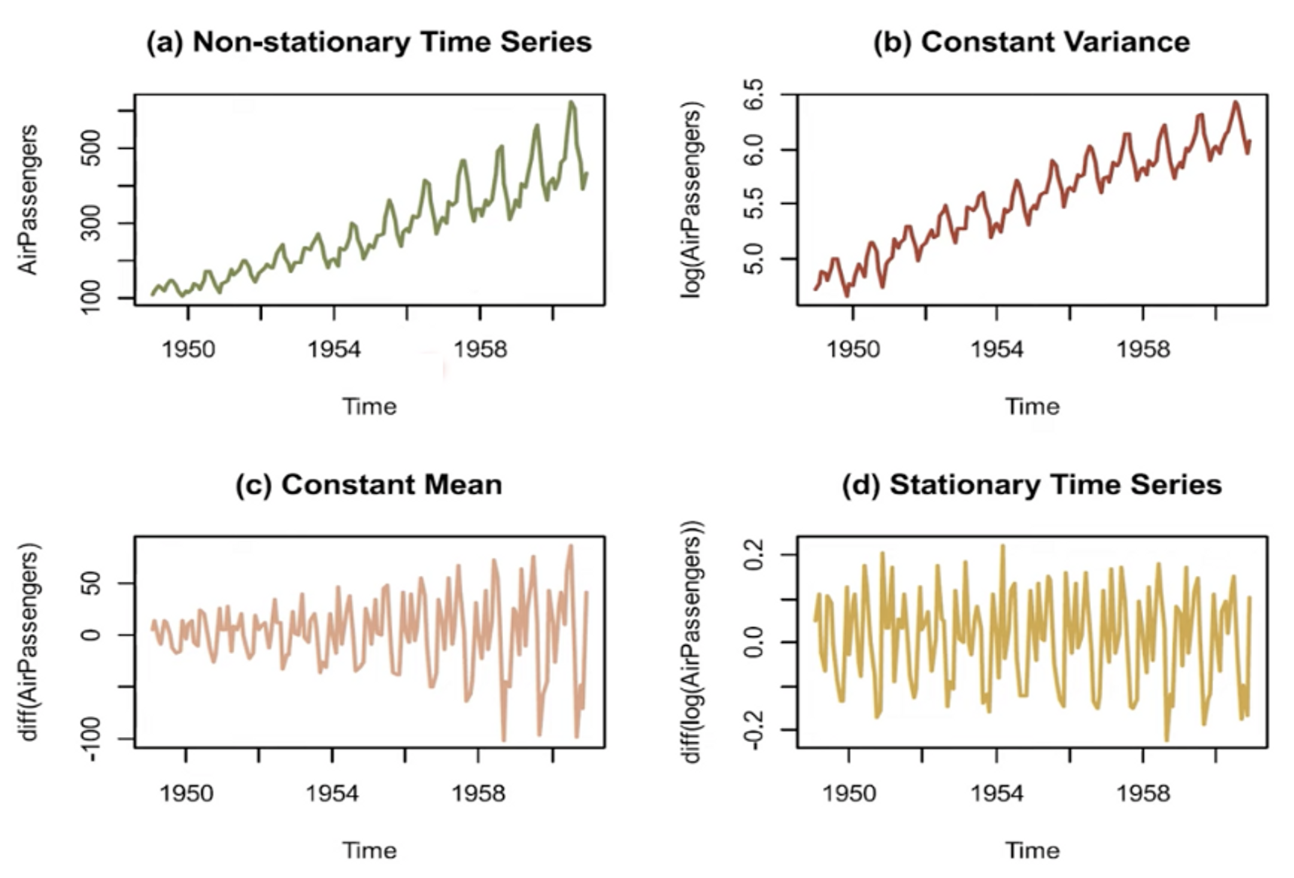
(a) : 비정상 시계열
-
(b) : 로그변환을 통해 변동폭 일정하게 변환
-
(c) : 차분을 통한 평균 일정한 정상 시계열로 변환
-
(d) : 로그변환, 차분 동시에 진행시켜 평균, 분산 일정한 정상 시계열로 변환
차분(differencing)
- 정상성을 나타내지 않는 시계열을 정상성을 나타내도록 만드는 한가지 방법
- 연이은 관측값들의 차이 계산하여 변동하는 평균을 제거하여 추세나 계절성 제거(혹은 감소)
- 정상성을 나타내는 시계열에서는 ACF가 빠르게 0으로 떨어지고, 정상성을 나타내지 않는 데이터에서 은 종종 큰 양수 값을 가짐
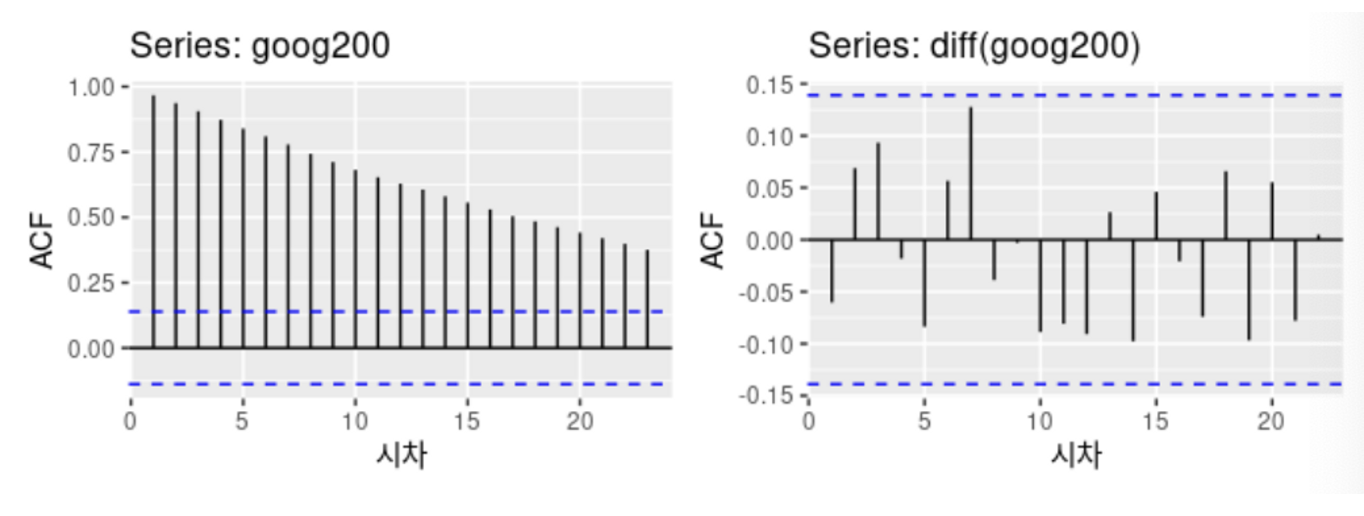
확률보행 모델(random walk)
- 첫번째 관측값에 대한 차분을 계산할 수 없어 차분을 구한 시계열은 개의 값만 가짐
- 차분을 구한 시계열이 백색잡음(, white noise)일 경우 시계열 모델을 정리한 것이 확률 보행(random walk) 모델
- 확률보행에는 다음과 같은 특징 존재
- 누가 봐도 알 수 있는 긴 주기를 갖는 상향/하향 추세 존재
- 갑작스럽고 예측할 수 없는 방향 변화 존재
2차 차분
- 차분을 통해 구한 데이터가 정상성이 없는 경우 한 번 더 차분 진행
- 이 경우 는 개의 값을 가짐
- 원본 데이터의 변화에서 나타나는 변화를 모델링 → 실제 상황에서는 잘 일어나지 않음
자기회귀 모델(AR(p))
- 변수의 과거 값의 선형 조합을 이용해 관심 있는 변수 예측
- 이전 자신의 관측값이 이후 자신의 관측값에 영향을 준다는 아이디어 기반
- 자기회귀(autoregressive) → 자기 자신에 대한 변수의 회귀
- 현재의 계열값이 일정한 시간 지연으로 이전 계열값에 따라 달라진다고 가정하고 시계열을 자신의 계열에 회귀
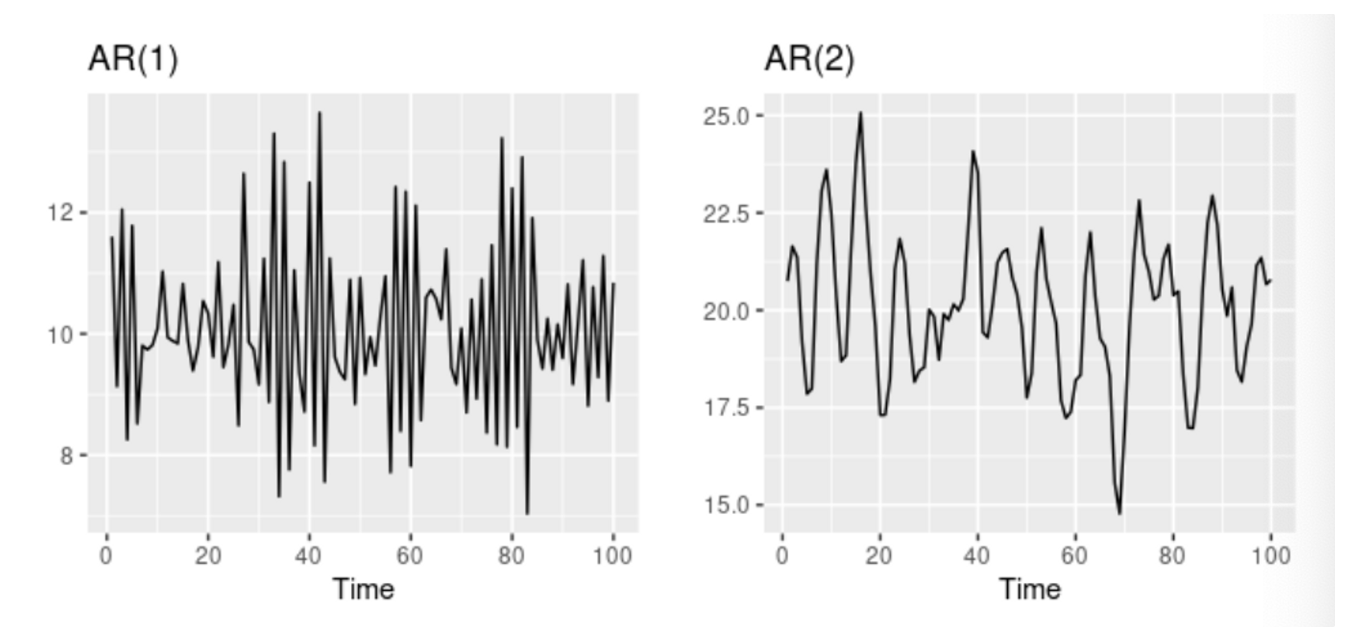
- AR(1)의 모델의 경우
- 인 경우 는 백색잡음
- 인 경우 는 확률보행 모델
- 인 경우 는 표류가 있는 확률보행 모델
- 인 경우 는 평균값을 중심으로 진동
- 보통 자기회귀 모델은 정상성을 나타내는 데이터에만 사용하는데, 이 경우 매개변수 값에 대한 몇가지 제한조건 존재
- AR(1) 모델 :
- AR(2) 모델 :
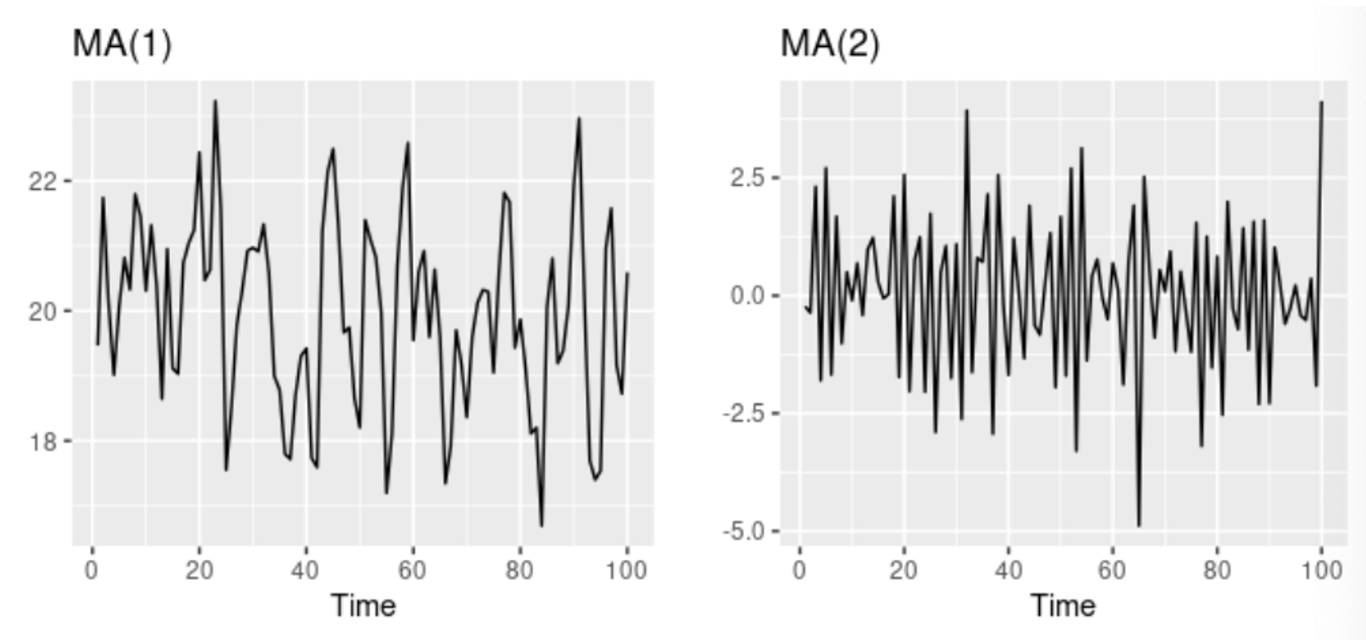
이동평균 모델(MA(q))
- 회귀처럼 보이는 모델에서 과거 예측 오차(forecast error) 이용하여 미래 예측
- 현재 오류가 일정한 시간 지연(q)으로 이전 오류에 따라 달라진다고 가정하고 시계열의 오류 모델링
- 의 각 값은 과거 몇개의 예측 오차(forecast error)의 가중 이동 평균
- AR(p) 모델을 MA(∞)모델로 쓸 수 있음
-
AR(1) 모델을 MA(∞) 모델로 바꾸기
-
위 과정을 반복할 경우 아래와 같은 MA(∞)식 나옴
-
- MA 매개변수에 몇몇 제한조건을 걸면 반대도 성립함. 즉, MA(q)과정을 AR(∞)과정으로 변환 가능. 이때 MA모델을 가역적(invertible)이라고 한다.
- 다른 모델에 대한 가역성의 제한조건은 아래와 같다
- MA(1) 모델 :
- MA(2) 모델 :
ARIMA 모델(ARIMA(p,d,q))
- : 한번 이상 차분을 구한 시계열
- : 자기회귀 부분의 차수, : 이동 평균 부분의 차수, : 1차 차분이 포함된 정도
ACF, PACF
- ARIMA 모델의 p,q를 확인하는 방법
1. ACF(AutoCorrelation Function)
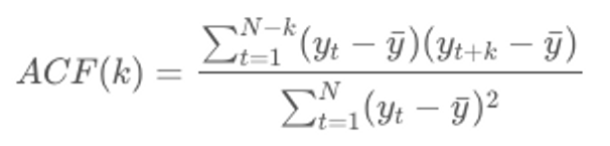
- 시차에 따른 일련의 자기상관, 시차 커질수록 ACF는 0에 수렴
- 정상 시계열일수록 빠르게 0에 수렴, 비정상 시계열일수록 천천히 감소하고 종종 큰 양의 값을 가짐
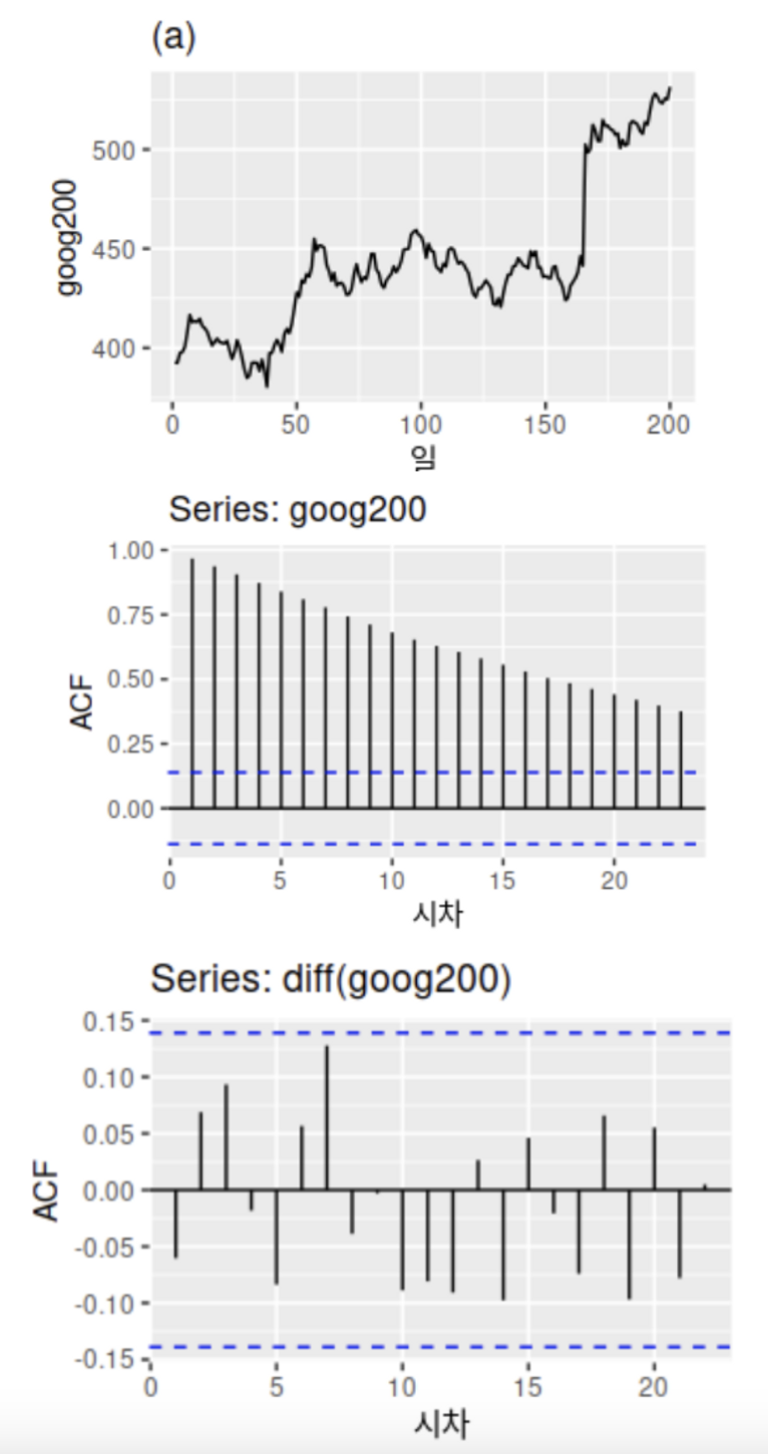
- 추세가 존재하는 비정상 시계열 데이터(첫번째 그림)의 ACF 그래프와(두번째 그림) 차분을 통해 정상 시계열로 변환 후 그린 ACF 그래프(세번째 그림)
- 추세가 존재하는 비정상 시계열 데이터(첫번째 그림)의 ACF 그래프와(두번째 그림) 차분을 통해 정상 시계열로 변환 후 그린 ACF 그래프(세번째 그림)
2. PACF(Partial AutoCorrelation Function)
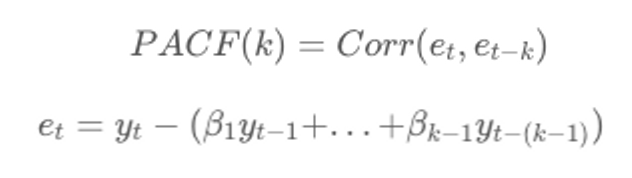
- 시차에 따른 일련의 편자기상관, 시차가 다른 두 시계열 데이터 간의 순수한 상호 연관성
- 와 간 순수한 상관관계로, 두 시점 사이에 포함된 시점의 데이터 영향 제거
3. 활용방법
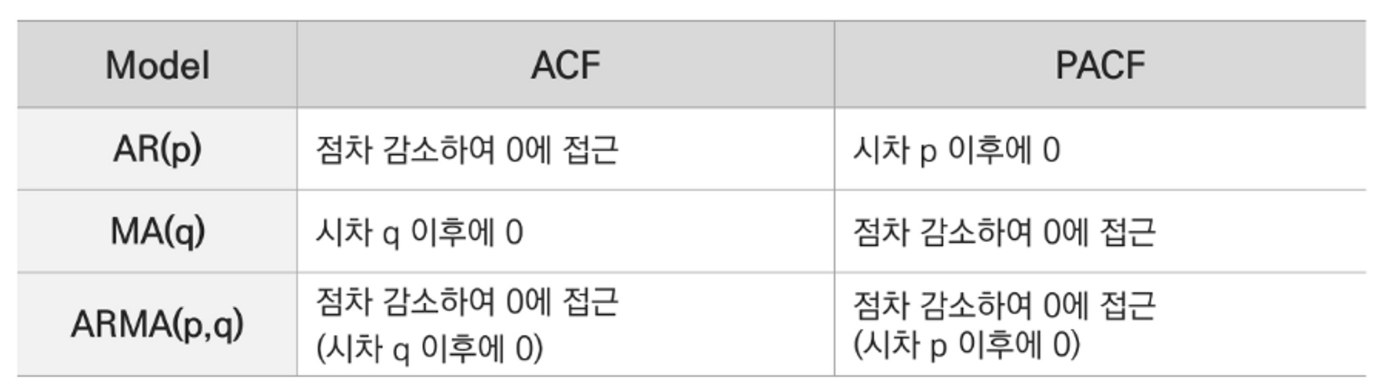
- 예시
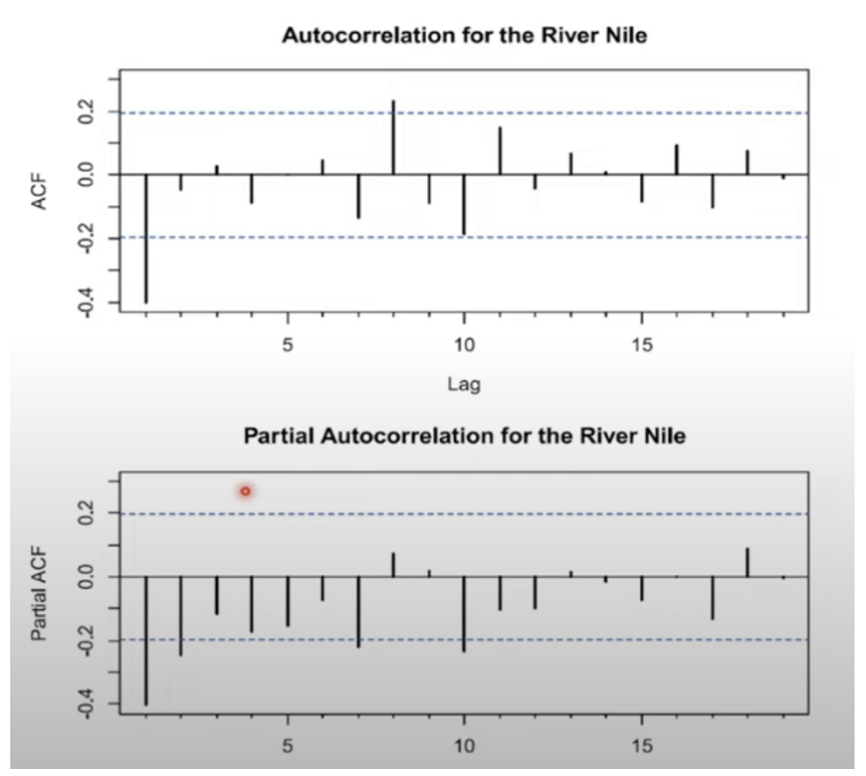
- 위의 ACF그래프의 경우 시차1 이후, PACF의 경우 시차2 이후 0에 수렴
- 또한 두 그래프 모두 점진적으로 0에 수렴 → 따라서 AR(2), MA(1), ARMA(2,1)등의 모델 활용 가능
