Chapter 2. 마르코프 결정 프로세스(Markov Decision Process)

순차적 의사결정 문제는 결국 MDP(Markov Decision Process)라는 개념을 통해 더 정확하게 표현 가능

2.1 마르코프 프로세스(Markov Process)

2.1.1 아이가 잠이 드는 마르코프 프로세스

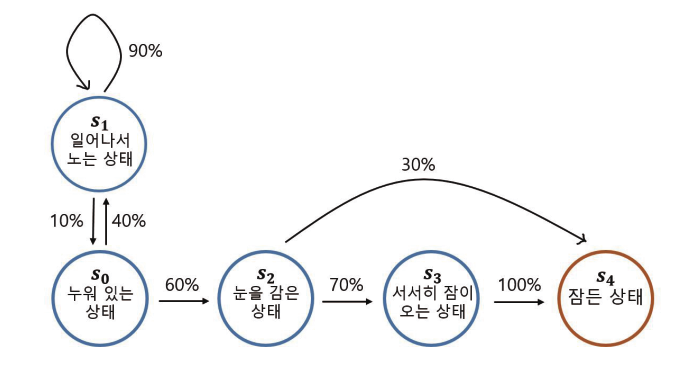
아이가 취할 수 있는 상태

• 누워 있는 상태 S0
• 일어나서 노는 상태 S1
• 눈을 감은 상태 S2
• 서서히 잠이 오는 상태 S3
• 잠든 상태 S4

하나의 상태에서 다른 상태로 상태 전이가 일어남
S4의 경우 종료 상태

MP(Markov Process)

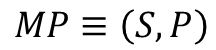
• 마르코프 프로세스는 상태(S)와 전이확률행렬(P)로 정의

2.1.2 마르코프 성질(Markov property)

마르코프 성질의 정의

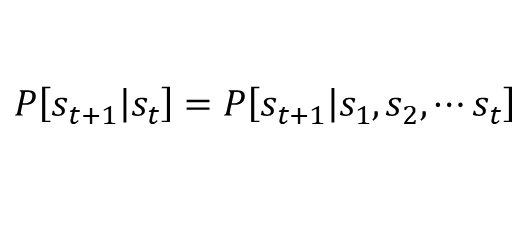
• 상태(St)일때 상태(St+1)로 전이 될 확률

마르코프 성질의 뜻

• "미래는 오로지 현재에 의해 결정된다."

• 상태(St)가 되기까지의 과정은 확률 계산에 영향 X

마르코프한 상태

• 체스 게임
  • 한 수 이전 혹은 그 전의 상황의 영향 X
  • 어느 시점 t의 사진 한 장으로 체스의 다음수 결정 가능

마르코프하지 않은 상태

• 운전하고 있는 운전자의 상태
  • 어느 시점 t의 사진 한 장으로 의사결정 불가능
  • 앞으로 가고 있는지, 뒤로 가는지 확인 불가
  • 10초 동안의 사진 10장을 묶어서 상태로 제공하면 좀 더 마르코프한 상태에 가깝
  • 진행 방향, 속도, 가속도 등의 정보를 함께 제공하여 마르코프한 상태 만족

--> 어떤 현상을 마르코프 프로세스로 모델링하려면 상태가 마르코프 해야하며, 단일 상태 정보만으로도 정보가 충분하도록 상태를 잘 구성해야 함

2.2 마르코프 리워드 프로세스(Markov Reward Process)

마르코프 프로세스에 보상의 개념이 추가되면 마르코프 리워드 프로세스(Markov Reward Process)

2.2.1 아이가 잠이 드는 MRP

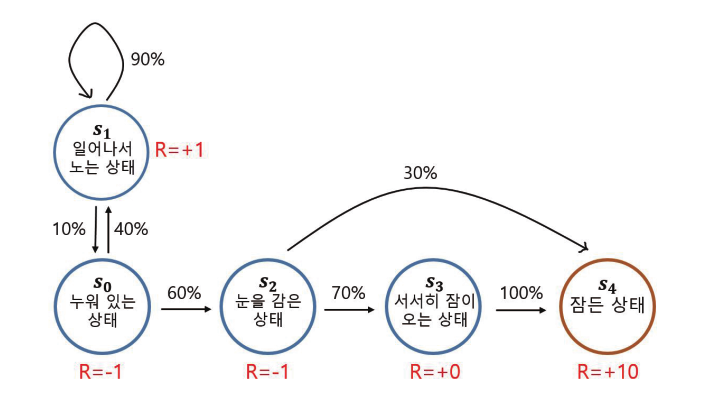
아이가 잠이 드는 MP에 빨간색으로 보상 값이 추가된 것

MRP(Markov Process)

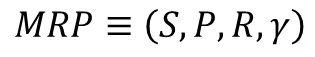
• 상태의 집합 S
  • 마르코프 프로세스의 S와 같고, 상태의 집합
• 전이 확률 행렬 P
  • 마르코프 프로세스의 P와 같고, 상태 s 에서 s'으로 갈 확률을 행렬 형태로 표현한 것
• 보상함수 R
  • 어떤 상태 S에 도착했을 때 받게 되는 보상
    
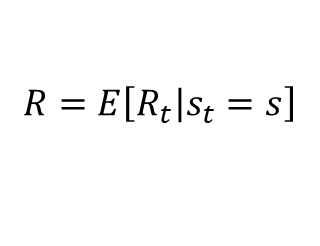
  • E(기댓값, 평균값)이 나오는 이유는 특정 상태에 도달했을때 받는 보상이 매번 조금씩 다를 수 있으므로
  • ex) 특정 상태에서 500원 동전을 던져서 앞면 : 500원, 뒷면 : 0원 => 기댓값 : 250원
• 감쇠인자 𝛾
  • 0< 𝛾 <1
  • 미래에 얻을 보상에 비해 당장 얻는 보상이 얼마나 더 중요하게 여길 것인지를 나타내는 파라미터
  • 미래에 얻을 보상의 값에 𝛾가 여러 번 곱해지면서 그 값을 작게 만드는 역할

2.2.2 감쇠된 보상의 합, 리턴

에피소드(Episode)

• MRP에서는 MP와 다르게 상태가 바뀔 때마다 해당하는 보상을 얻음
• 상태 S0에서 보상 R0를 받고 시작하여 종료 상태인 St에 도착할 때 보상 Rt를 받으며 끝남
• S0에서 St까지 가는 여정을 다음과 같이 표현

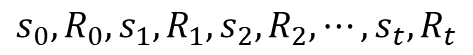
리턴 (G)

• 현재 타임스텝이 t일때 그 이후에 발생하는 모든 보상의 값
• 강화학습은 리턴을 최대화하도록 학습
  

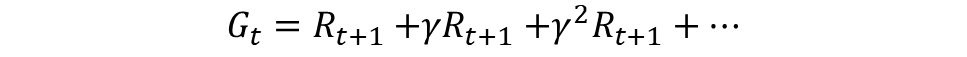
2.2.3 𝛾는 왜 필요할까?

• 𝛾=0 일때 미래의 보상은 모두 0 --> 매우 근시안적인 에이전트
• 𝛾=1 일때 매우 장기적인 시야를 갖고 움직이는 에이전트

1. 수학적 편리성

• 𝛾를 1보다 작게 해줌으로써 리턴 Gt가 무한의 값을 가지는 것을 방지

2. 사람의 선호 반영

• 사람은 기본적으로 당장 벌어지는 눈앞의 보상을 더 선호
• 에이전트를 학습하는데 있어서 이를 반영

3. 미래에 대한 불확실성 반영

• 현재와 미래 사이에는 다양한 확률적 요소
• 당장 느끼는 가치에 비해 미래에 느끼는 가치 변화 가능
• 미래의 가치에는 불확실성을 반영하고자 감쇠 인자 사용

2.2.4 MRP에서 각 상태의 밸류(Value) 평가하기

• 어떤 상태를 평가할 때에는 그 시점으로부터 미래에 일어날 보상을 기준으로 평가
• MRP 자체가 확률적인 요소에 의해 다음 상태가 정해지므로 리턴 역시 매번 변화
• --> 리턴의 기댓값 사용

2.2.5 에피소드의 샘플링

• 하나의 에피소드 안에서 경유하는 상태들은 매번 다름
• 매번 에피소드가 어떻게 샘플링 되느냐에 따라서 리턴 달라짐

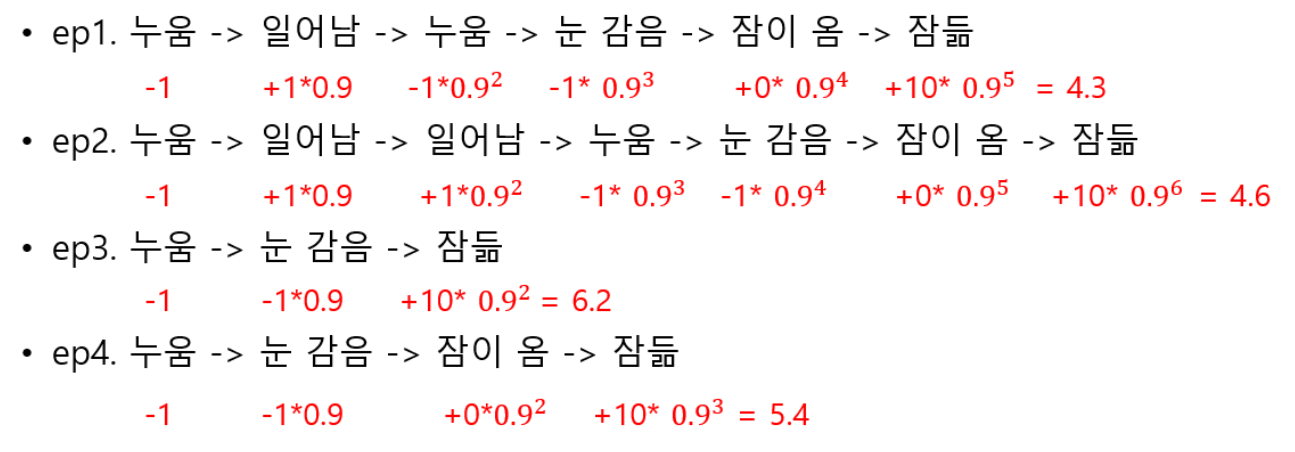
에피소드 샘플

ep1. 누움 -> 일어남 -> 누움 -> 눈 감음 -> 잠이 옴 -> 잠듦
ep2. 누움 -> 일어남 -> 일어남 -> 누움 -> 눈 감음 -> 잠이 옴 -> 잠듦
ep3. 누움 -> 눈 감음 -> 잠듦
ep4. 누움 -> 눈 감음 -> 잠이 옴 -> 잠듦

2.2.6 상태 가치 함수(State Value Function)

• 상태를 인풋으로 넣으면 그 상태의 Value를 아웃풋으로 출력하는 함수
• 상태 s로부터 시작하여 얻는 리턴의 기댓값

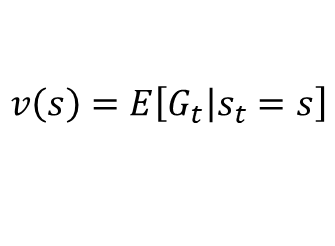
• 에피소드 4개를 샘플링 및 리턴 계산

2.3 마르코프 결정 프로세스(Markov Decision Process)

• 앞의 MP와 MRP에서는 상태 변화가 자동으로 이루어짐
• 순차적 의사 결정에서는 의사결정이 핵심

2.3.1 MDP의 정의

• MRP에 에이전트가 더해진 것
• 에이전트는 각 상황마다 액션
• 해당 액션에 의해 상태가 변하고 그에 따른 보상

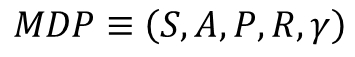
• 상태의 집합 S

  • MP와 MRP에서의 S와 동일

• 액션의 집합 A

  • 에이전트가 취할 수 있는 액션들
  • ex) 화성의 흙을 채집하는 탐사 로봇 --> A={앞으로 이동, 뒤로 이동, 흙 채집}
  • 에이전트는 스텝마다 액션중 하나를 취하며 그대따라 상태 변화

• 전이 확률 행렬 P

  • 현재 상태 s이며 에이전트가 액션 a를 선택했을때 다음 상태가 s'이 될 확률
  • 같은 상태 s에서 같은 액션 a를 선택해도 매번 다른 상태에 도착할 수도 있음

  

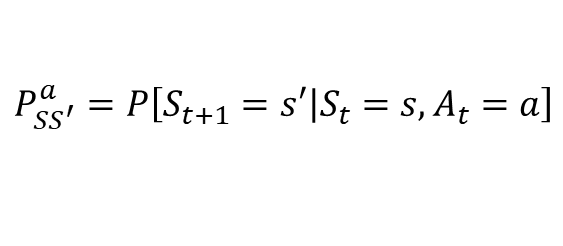
• 보상함수 R

  • 현재 상태 s이며 에이전트가 액션 a를 선택했을때 받는 보상의 기댓값

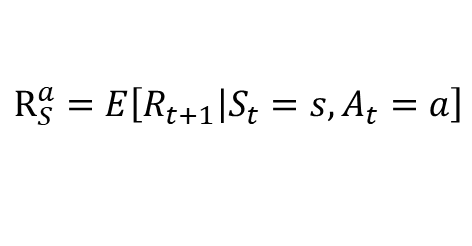
• 감쇠인자 𝛾
  • MRP에서의 𝛾과 동일

2.3.2 아이 재우기 MDP

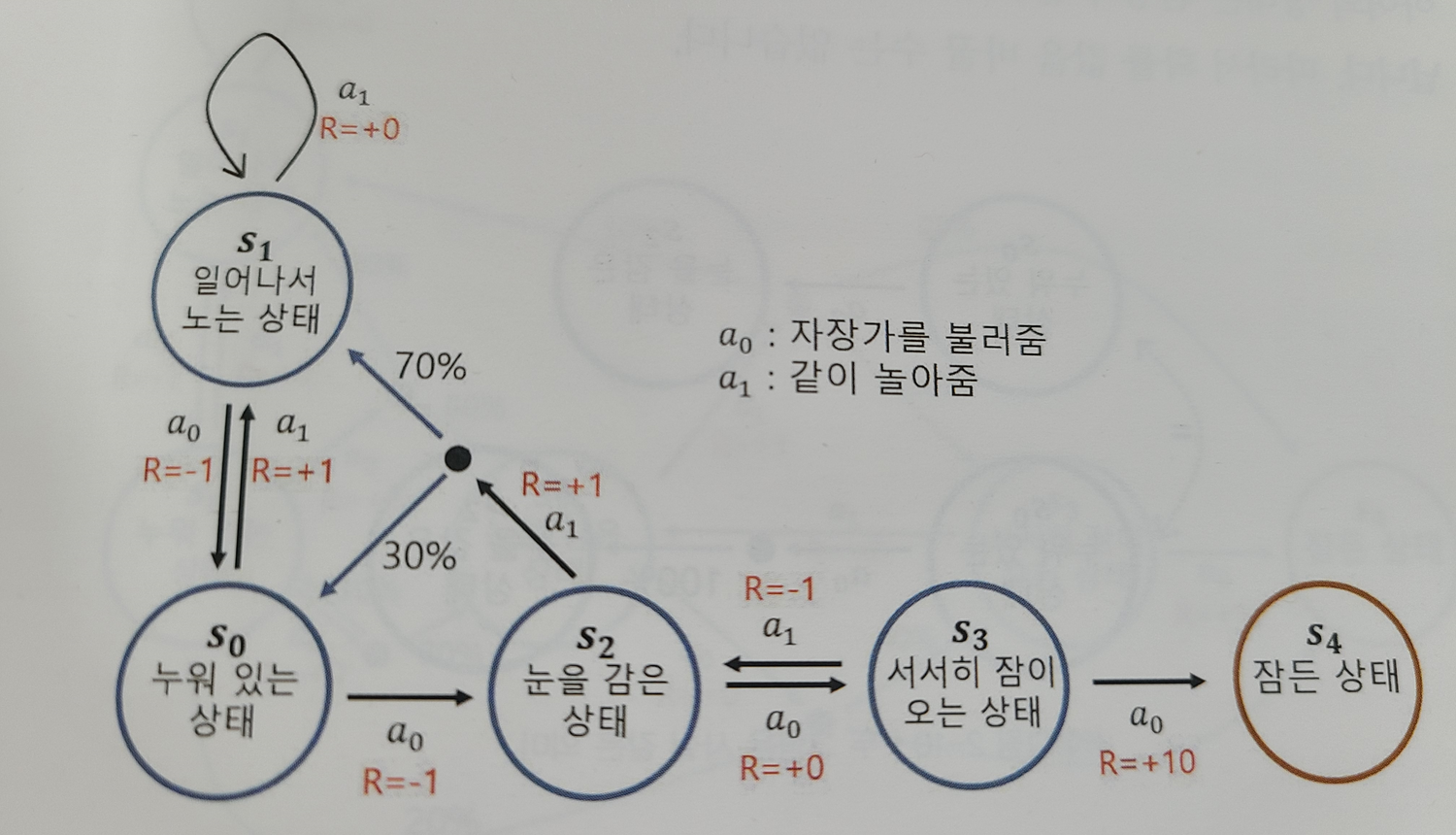
• 에이전트 개입 시작
• 상태 S일때 액션 a를 하면 확률적으로 다음 상태가 결정
• A ={ a0 : "자장가를 불러줌", a1 : "같이 놀아줌"}
• 상태 S2에서의 전이 확률 수식

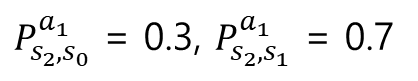
• 실제 상황에서는 상태의 개수가 훨씬 많고, 액션의 수도 훨씬 다양
  --> 각 상태 S에 따라 어떤 액션 a를 선택해야 보상의 합을 최대로 할 수 있는가?

2.3.3 정책 함수와 2가지 가치 함수

정책함수

• 각 상태에서 어떤 액션을 선택할지 정해주는 함수
• 𝜋를 사용해서 표기

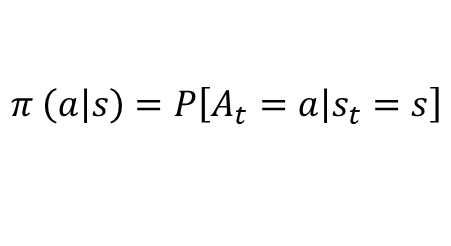
• 상태 s에서 액션 a를 선택할 확률
• 상태 s에서 선택할 수 있는 액션이 a0, a1, a2라고 할때

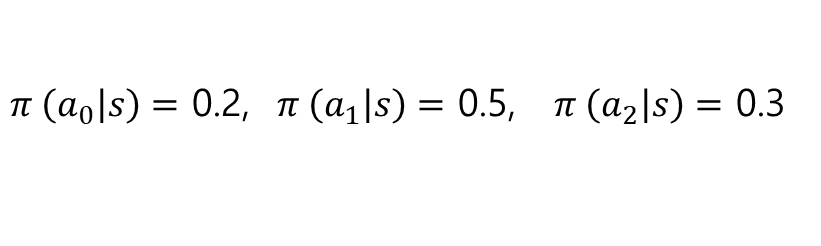
• 위와 같이 각각 액션에 대해 얼마큼 확률을 부여할지를 정책 함수가 결정

상태 가치 함수

• 주어진 상태에서 미래에 얻을 리턴의 기댓값을 상태의 벨류로 정의 했었고, 이와 비슷
• 에이전트의 액션과 정책함수가 도입
• 주어진 상태에서 정책함수에 의해서 정해지는 액션에 따라 얻어지는 리턴의 기댓값

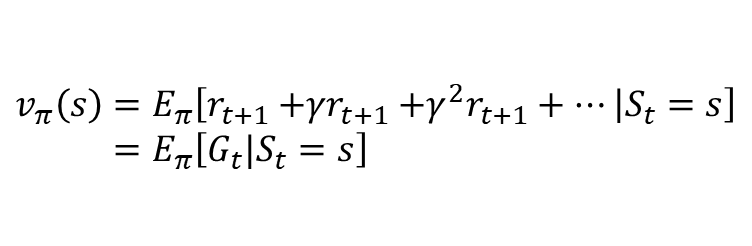
• s부터 끝까지 𝜋를 따라서 움직일 때 얻는 리턴의 기댓값
• 가치함수는 𝜋에 의존적

액션 가치 함수

• 액션을 평가할 수 있다면 각 상태에서 선택할 수 있는 액션을 모두 평가해 본 후 가장 가치있는 액션을 선택
• 인풋으로 s와 a가 포함
• s0에서 a0와 s2에서 a0은 전혀 다른 상황이므로 상태 s와 결합하여 평가

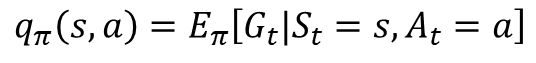
• s에서 a를 선택하고, 그 이후에는 𝜋를 따라서 움직일 때 얻는 리턴의 기댓값
• 여러 액션중 하나를 선택했을때, 리턴의 기댓값이 가장 높은 액션이 가장 가치 있는 액션

상태 가치 함수와 액션 가치 함수의 차이는 "s에서 어떤 액션을 선택하는가" 부분에만 차이

2.4 Prediction과 Control

1. Prediction : 𝜋가 주어졌을 때 각 상태의 밸류를 평가하는 문제

• --> 임의의 정책 𝜋에 대해 각 상태의 Value를 구하는 것

2. Control : 최적 정책 𝜋*를 찾는 문제

• --> 누구를 만나도 다 이기는 정책

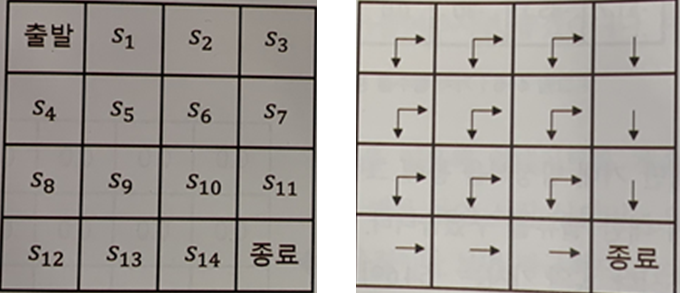
최적 정책 𝜋* 과 최적 가치 함수 v* 를 찾으면 이 MDP는 풀렸다
--> MDP의 최적 정책과 최적 가치 함수를 찾아내어 MDP를 푸는 것이 목적