극댓값 찾기
1차원의 경우
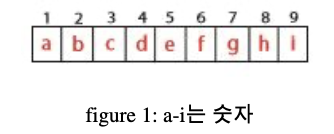
b>=a이고 b>=c이면 2번 위치가 극댓값이다.
i>=h이면 9번 위치가 극댓값이다.
문제 : 극댓값이 존재할 경우 그 값을 찾아라. (항상 존재하는가?)
간단한 알고리즘
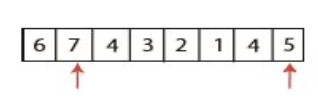
왼쪽부터 시작하는 경우
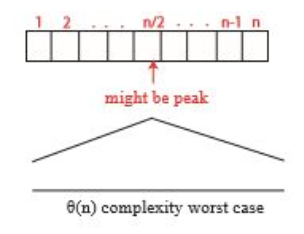
중앙부터 시작하면 어떻게 될까?
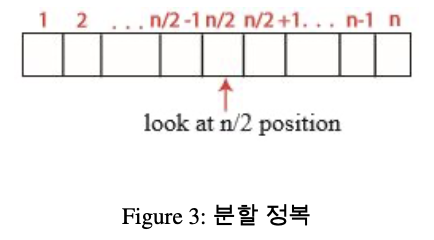
아래 그림과 같은 상황에서는 n/2개의 원소를 확인해야 한다.
중앙부터 시작하여 인접한 원소 중 중앙 원소보다 값이 큰 쪽으로 방향을 선택한다면, n/2개보다 더 많이 확인해야 할 경우가 있을까?
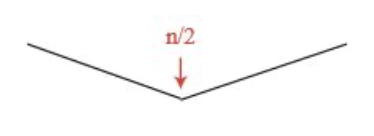
더 효율적으로 찾을 수 있을까?
-
a[n/2] < a[n/2-1]이면 왼쪽 절반인 1부터 n/2-1까지 보고 극댓값을 찾는다.
-
그게 아니면 a[n/2] < a[n/2+1]이면 오른쪽 절반인 n/2+1부터 n까지 보고 극댓값을 찾는다.
-
그것도 아니면 n/2 위치가 극댓값이다.
-
a[n/2] >= a[n/2-1], a[n/2] >= a[n/2+1]
-> 이 경우 복잡도는?
T(n) = T(n/2) + O(1) = O(1) + ..... + O(1) (log(n) times) = O(log(n))
(O(1)은 극댓값을 확인하는 부분)
-
위와 같이 O(i)들을 합하려면, 모든 경우에 적용되는 상수를 찾아야 한다.
-
n=1000000인 경우, 파이썬에서 O(n) 알고리즘을 실행하는 데 13초가 걸린다.
-
O(log n)알고리즘은 0.001초밖에 걸리지 않는다.
2차원의 경우
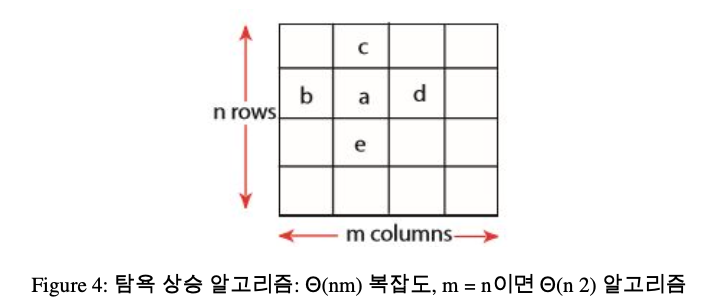
a >= b, a >= d, a >= c, a >= e이면 a는 2차원 극댓값이다.
시도 #1 : 1차원 분할 정복을 2차원으로 확장
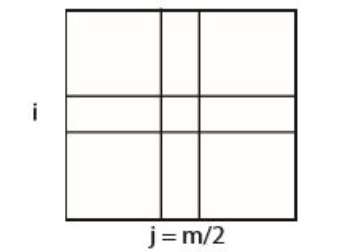
-
중앙 열 j = m/2을 선택한다.
-
(i, j)에서 1차원 극댓값을 발견한다.
-
(i, j)를 시작 지점으로 하여 i행에서 1차원 극댓값을 찾는다.
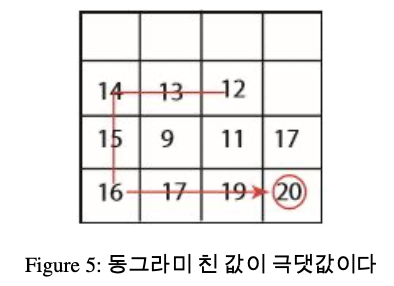
시도 #1 실패
-
문제 : 2차원 극댓값이 i행에 존재하지 않을 수도 있다.
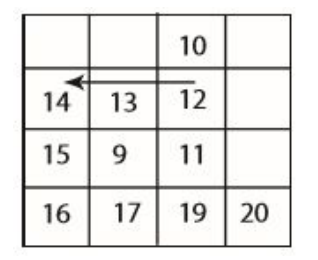
-
2차원 극댓값이 아닌 14를 찾음.
시도 #2
-
중앙 열 j=m/2을 선택한다.
-
(i, j)에서 j열의 최댓값을 찾는다.
-
(i, j-1), (i, j), (i, j+1)를 비교한다.
-
(i, j-1) > (i, j)이면 왼쪽 열을 선택한다.
-
오른쪽도 똑같이 진행한다.
-
두 조건 모두 만족하지 않으면, (i, j)가 2차원 극댓값이다.
-
열 개수가 절반으로 줄어든 새로운 문제를 푼다.
-
열이 1개 남으면, 최댓값을 찾고 끝난다.
시도 #2 예시
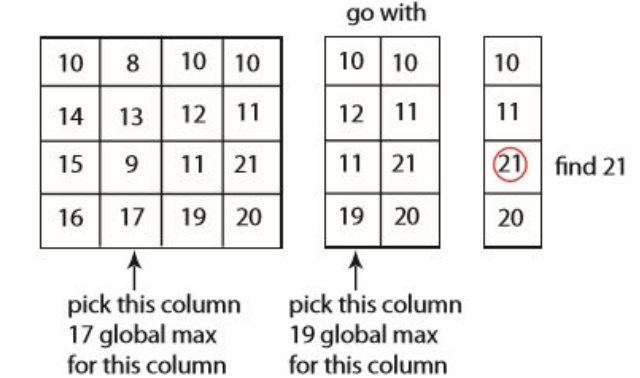
시도 #2 복잡도
n개의 행과 m개의 열이 있는 문제를 해결하기 위해 요구되는 일의 양을 T(n, m)라고 하면,
T(n, m) = T(n, m/2) + O(n) (to find global maximum on a column - (n rows))
T(n, m) = O(n) + ........ + O(n) = O(n log m) = O(n log n) if m = n
