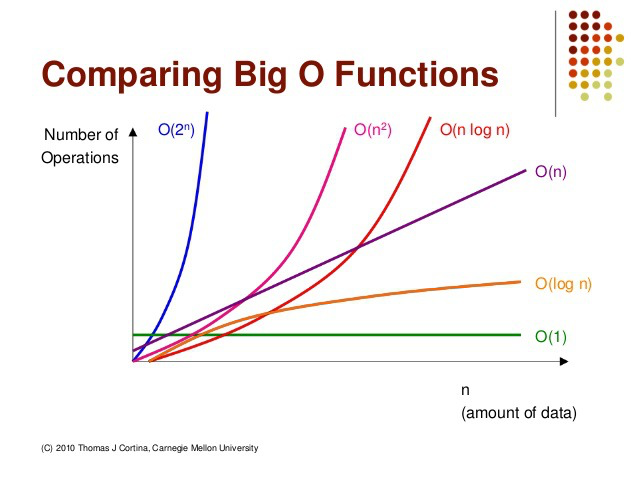
빅-오 표기법(Big-O Notation)
- 빅오란 입력값이 무한대로 향할때 함수의 상한을 설명하는 수학적 표기 방법이다.
- 빅오는 점근적 실행 시간(시간 복잡도)을 표기할때 가장 널리 쓰이는 수학적 표기 방법이다.
- 빅오 표기법은 알고리즘 효율성을 상한선 기준으로 표기한다.
빅-오 표기법의 특징
- 상수항 무시
- 영향력 없는 항 무시
- ->
- ->
- ->
대표적인 빅-오
1. 상수형 빅-오
- 데이터 수에 상관없이 연산횟수가 고정인 유형의 알고리즘이다.
- 연산횟수가 3이라 할지라도 (1)을 쓴다.
-> 상수형 빅-오는 연산횟수가 고정인 유형의 알고리즘을 대표하기 때문이다. - 상수값이 상상이상으로 클 경우 사실상 일정한 시간의 의미가 없다.
-> 최고의 알고리즘이 될 수 있지만 그만큼 신중해야 한다. - ex) 스택에서 push, pop
2. 로그형 빅-오
- 데이터 수의 증가율에 비해서 연산횟수의 증가율이 훨씬 낮은 알고리즘이다.
-> 바람직한 유형 - ex) 이진 탐색
3. 선형 빅-오
- 데이터의 수와 연산횟수가 비례하는 알고리즘이다.
- 모든 입력값을 적어도 한 번 이상 살펴봐야 한다.
- ex) for문
4. 선형로그형 빅-오
- 데이터의 수가 두배로 늘때, 연산횟수는 두배를 조금 넘게 증가하는 알고리즘이다.
- 대부분 효율이 좋은 알고리즘이 이에 해당한다.
- 입력값이 최선일 경우, 비교를 건너 뛰어 이 될 수 있다.
- ex) 퀵 정렬, 병합정렬, 힙 정렬
5. 제곱형 빅-오
,
- 제곱, 세제곱에 해당하는 연산횟수를 요구하는 알고리즘이다.
- 이중, 삼중으로 중첩된 반복문의 사용형태라고 볼 수 있다.
- ex) 이중 for문, 삽입정렬, 버블정렬, 선택정렬
6. 지수형 빅-오
- 지수적증가라는 매우 안좋은 연산횟수의 증가를 보이는 알고리즘이다.
- 사용하기에 매우 무리가 있고 비현실적이다.
- ex) 피보나치 수열
빅-오 표기들의 성능