Data Structure | Queue (js)

큐 (Queue)

: 데이터 입출력이 FIFO(선입선출) 형태로 일어나는 자료구조

스택과 달리 입구와 출구가 다름
삽입이 일어나는 곳ㅡ후단
삭제가 일어나는 곳ㅡ전단

front는 큐의 첫번째 요소를 가리키고
rear는 마지막 요소를 가리킴

✅ 선형 큐
큐의 공간이 제한된 상태에서, 데이터를 삽입하고 삭제하면서 front와 tail 인덱스가 계속 증가함

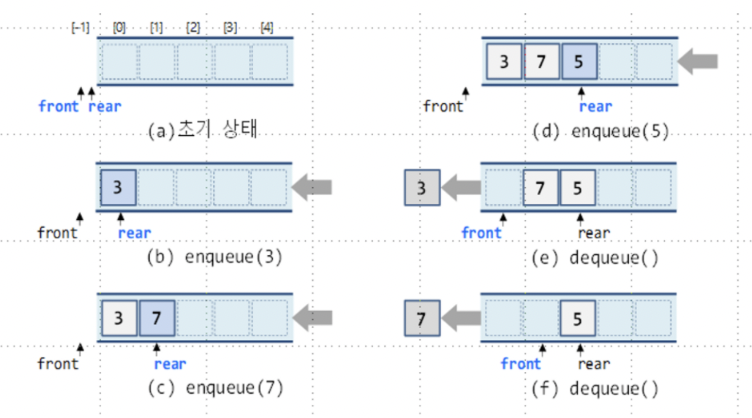
• ADT
  • 객체: 두 가지 끝(front, rear)이 있으며, FIFO(First In, First Out) 규칙에 따라 동작하는 요소들의 모음
  • 연산:
    isEmpty(): 큐가 비어 있는지 확인 / 큐가 비어 있으면 true, 그렇지 않으면 false를 반환
    enqueue(data): 큐의 rear에 요소를 추가하는 연산
    dequeue(): 큐의 front에서 요소를 제거하고 반환하는 연산
    peek(): 큐의 front에 있는 요소를 확인하는 연산. 큐에서 제거하지는 않음
    getLength(): 큐에 있는 요소의 개수를 반환하는 연산
    clear(): 큐를 초기화하여 모든 요소를 제거하는 연산
    display(): 큐에 있는 모든 요소를 출력하는 연산. 디버깅 목적으로 사용

큐를 front, rear 포인터를 가진 연결리스트나, frontIndex,rearIndex 키를 가진 dictionary로 구현하면 삽입,삭제 연산이 O(1)의 시간 복잡도 가짐

+딕셔너리로 구현한 큐에서 frontIndex와 rearIndex 키를 사용하면 삭제(dequeue) 연산의 경우, 딕셔너리에서 요소를 삭제하는 것이 일반적으로 O(1)에 가까운 시간이 걸리지만, 메모리에서 실제로 해제되는 방식에 따라 구현 세부 사항에 따라 최악의 경우 O(n)이 될 수 있음.

• dictionary

class Queue{
  constructor(){
    this.datas = {};
    this.frontIdx = 0; // 가장 앞의 요소
    this.rearIdx = -1; // 비어있음을 나타냄 - 가장 뒤의 요소
  }
  isEmpty(){
    return this.frontIdx > this.rearIdx; 
  }
  enqueue(data){
    this.rearIdx++;
    this.datas[this.rearIdx] = data;
  }
  dequeue(){
    if(this.isEmpty()){
      console.log('Queue is Empty!');
      return;
    }
    const data = this.datas[this.frontIdx];
    delete this.datas[this.frontIdx];
    this.frontIdx++;
    return data;
  }
  peek(){
    if(this.isEmpty()){
      console.log('Queue is Empty!');
      return;
    }
    return this.datas[this.frontIdx]
  }
  getLength(){
    return this.isEmpty() ? 0 : this.rearIdx-this.frontIdx+1;
  }
  display(){
    if(this.isEmpty()){
      console.log('Queue is Empty!');
      return;
    }
    else{
      for(let i = this.frontIdx; i<this.rearIdx; i++){
        console.log(this.datas[i]);
      }
    }
  }
}

• 링크드 리스트

class Node {
  constructor(data) {
    this.data = data;
    this.next = null;
  }
}

class Queue{
  constructor(){
    this.front = null;
    this.rear = null;
    this.size = 0;
  }
  isEmpty(){
    return this.size === 0; 
  }
  enqueue(data){
    const newNode = new Node(data);
    if(this.isEmpty()){
      this.front = newNode;
      this.rear = newNode;
    } else {
      this.rear.next = newNode; // 기존 rear의 next를 새 노드로 설정
      this.rear = newNode; // rear를 새 노드로 갱신
    }
    this.size++;
  }
  dequeue(){
    if(this.isEmpty()){
      console.log('Queue is Empty!');
      return;
    }
    const dequeueNode = this.front;
    this.front = this.front.next; 
    if(!this.front) this.rear = null; //요소 하나였을때 -> 빈 큐가 됨
    this.size--;
    return dequeueNode.data;
  }
  peek(){
    if(this.isEmpty()){
      console.log('Queue is Empty!');
      return;
    }
    return this.front.data;
  }
  getLength(){
    return this.size;
  }
  clear(){
    this.front = null;
    this.rear = null;
    this.size = 0;
  }
  display(){
    if(this.isEmpty()){
      console.log('Queue is Empty!');
      return;
    }
    let current = this.front;
    while(current){
      console.log(current.data);
      current=current.next;
    }
  }
}

// 출력 확인
const queue = new Queue();
queue.enqueue(10);
queue.enqueue(20);
queue.enqueue(30);
queue.display(); // 10, 20, 30 출력
console.log(queue.dequeue()); // 10 반환 및 삭제
console.log(queue.peek());    // 20 출력
console.log(queue.getLength()); // 2 출력 (20, 30)
queue.display(); // 20, 30 출력

✅ 원형 큐: 선형 큐와 달리 처음과 끝이 연결된 원형으로 공간을 재사용함 -> 고정된 크기의 큐에서의 공간 낭비를 줄임
rear가 리스트의 끝에 도달한 후에는 다시 처음 위치에서 빈 공간을 채우며 삽입과 삭제가 일어남 / rear, front 위치계산을 위해 하나의 빈 공간 필요 - 실제 큐의 크기는 큐에서 1을 뺀 크기

front, rear의 초기값이 0 / front는 항상 첫번째 요소, rear는 마지막 요소를 가리킴
front==rear 이면 공백상태
front가 rear 바로 다음이면, 즉 (rear+1)%maxSize 와 같으면 포화상태

• dictionary

class CircularQueue{
  constructor(maxSize){
    this.maxSize = maxSize;
    this.datas = {};
    this.frontIdx = 0;
    this.rearIdx = 0;
  }
  isEmpty(){
    return this.frontIdx === this.rearIdx; 
  }
  isFull(){
    return (this.rearIdx + 1) % this.maxSize === this.frontIdx;
  }
  enqueue(data){
    if(this.isFull()){
      console.log('Queue is Full!');
      return;
    }
    this.rearIdx = (this.rearIdx+1) % this.maxSize;
    this.datas[this.rearIdx] = data;
  }
  dequeue(){
    if(this.isEmpty()){
      console.log('Queue is Empty!');
      return;
    }
    this.frontIdx = (this.frontIdx+1) % this.maxSize;
    const data = this.datas[this.frontIdx];
    delete this.datas[this.frontIdx];
    return data;
  }
  peek(){
    if(this.isEmpty()){
      console.log('Queue is Empty!');
      return;
    }
    return this.datas[(this.frontIdx+1) % this.maxSize];
  }
  getLength(){
    return (this.rearIdx - this.frontIdx + this.maxSize) % this.maxSize;
  }
  display(){
    if(this.isEmpty()){
        console.log('queue is empty!');
        return;
    }
    let i = this.frontIdx;
    while(i != this.rearIdx){
      i = (i+1) % this.maxSize; 
      console.log(this.datas[i]);
    }
  }
}

• 링크드 리스트

class Node {
  constructor(data) {
    this.data = data;
    this.next = null;
  }
}

class CircularQueue{
  constructor(maxSize){
    this.maxSize = maxSize;
    this.front = new Node(null); // 더미 노드
    this.front.next = this.front; // 원형으로 만듦
    this.rear = null;
    this.size = 0;
  }
  isEmpty(){
    return this.size === 0;
  }
  isFull(){
    return this.size === this.maxSize;
  }
  enqueue(data){
    if(this.isFull()){
      console.log('Queue is Full!');
      return;
    }
    const newNode = new Node(data);
    
    if(this.isEmpty()){
      this.front.next = newNode;
      newNode.next = this.front; // 원형으로 만듦
      this.rear = newNode;
    }
    else{
      newNode.next = this.front.next; // 새 노드가 front 뒤를 가리킴
      this.rear.next = newNode; // 기존 rear가 새 노드를 가리킴 - 실제 첫 번째 요소는 front.next
      this.rear = newNode; // rear를 새 노드로 갱신
    }
    this.size++;
  }
  dequeue(){
    if(this.isEmpty()){
      console.log('Queue is Empty!');
      return;
    }
    const deqeueNode = this.front.next;
    if (this.front.next === this.rear) { // 큐에 원소가 하나만 있을 때
      this.front.next = this.front;
      this.rear = null;
    } else {
      // front를 다음 노드로 옮김
      this.front.next = this.front.next.next;
    }
    this.size--;
    return deaueueNode.data;
  }
  peek(){
    if(this.isEmpty()) return null; 
    return this.front.next.data;
  }
  getLength(){
    return this.size;
  }
  clear(){
    this.front.next = this.front;
    this.rear = null;
    this.size = 0;
  }
  display(){
    if(this.isEmpty()){
      console.log('queue is empty!');
      return;
    }
    let current = this.front.next;
    while(current != this.front){
      console.log(current.data);
      current=current.next;
    }
  }
}

// 출력 확인
const cQueue = new CircularQueue(3);
cQueue.enqueue(10);
cQueue.enqueue(20);
cQueue.enqueue(30); // Queue is Full! 출력
cQueue.display(); // 10, 20 출력
console.log(cQueue.dequeue()); // 10 반환 및 삭제
console.log(cQueue.peek());    // 20 출력
console.log(cQueue.getLength()); // 1 출력 (20)
cQueue.display(); // 20 출력

✅ 우선 순위 큐(priority queue): 우선 순위에 따라 데이터를 추출하는 자료구조

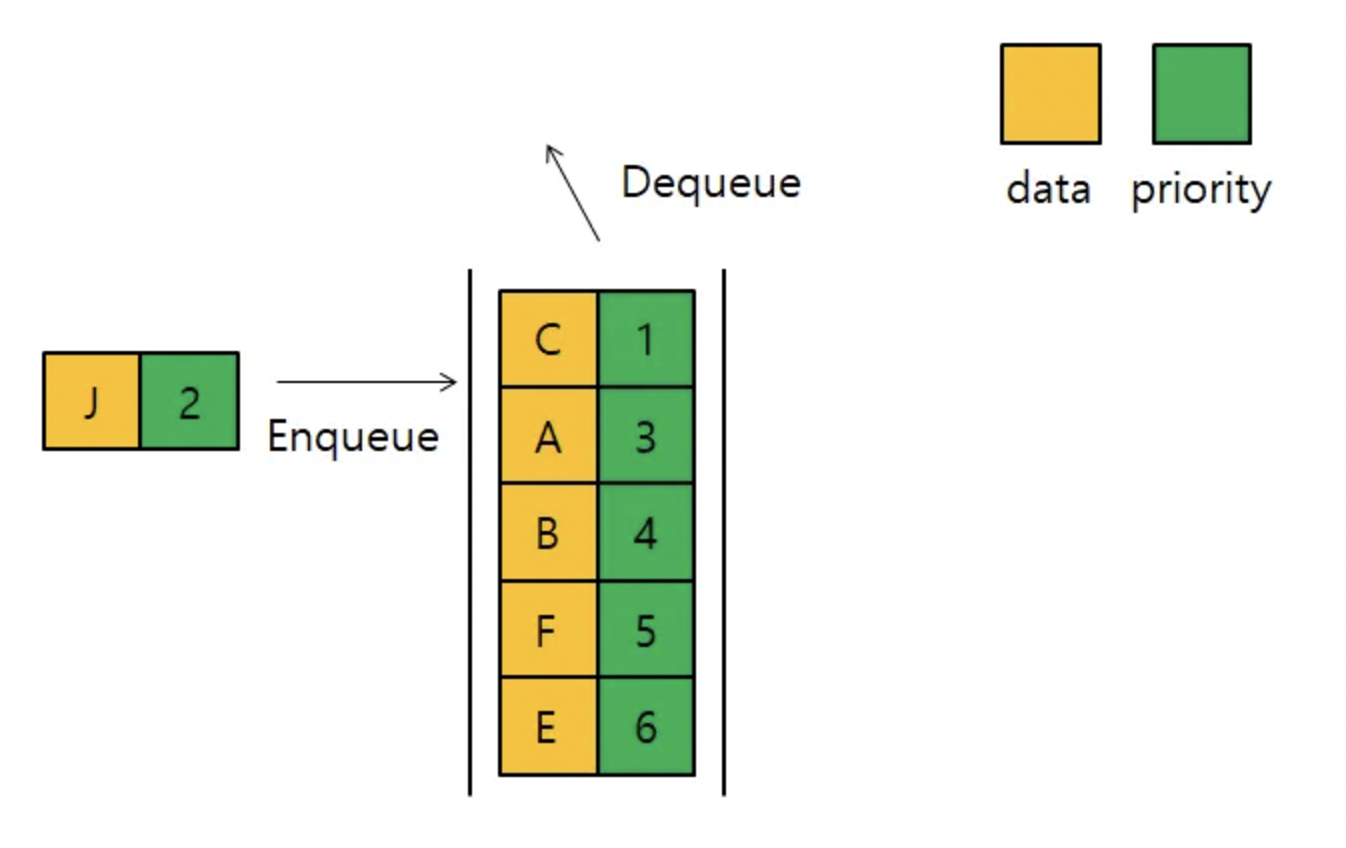
이진 트리 구조를 가짐
모든 항목에 우선 순위가 있고, 우선 순위가 높은 요소가 낮은 요소보다 먼저 queue에서 제외됨, 두 요소의 우선 순위가 같으면 queue에 들어온 순서에 따라 제외됨

각 요소는 총 2개의 데이터(값, 우선순위)를 가지고 있음
삽입 및 삭제 시 우선순위에 따라 요소들을 정렬해야하기 때문에 주로 힙(Heap) 구조로 구현됨

시간복잡도 (구현방식에 따라 달라짐)

+Heap: 원소들 중 최댓값, 최솟값을 빠르게 찾아내는 자료구조
완전 이진 트리 구조 /반정렬상태(느슨한 정렬 상태) 유지_부모 노드의 키값이 항상 자식노드의 키값 이상 or 이하인 이진트리임(최대힙, 최소힙) / 힙 트리에서는 중복값 허용함

힙에서 부모노드와 자식노드의 관계

• 왼쪽 자식의 인덱스===(부모의 인덱스)*2
• 오른쪽 자식의 인덱스===(부모의 인덱스)*2+1
• 부모의 인덱스===Math.floor(자식의 인덱스/2)

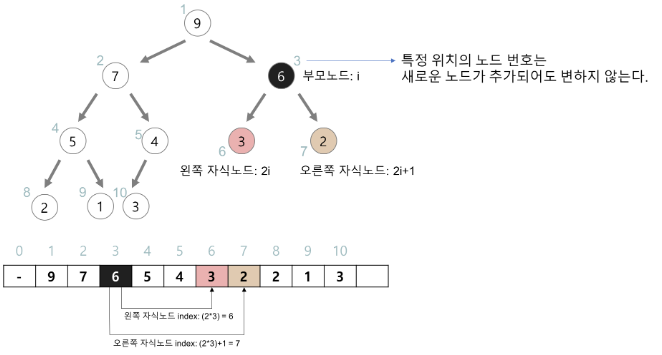
max heap: 값이 큰 원소부터 추출, 부모 노드 키값이 항상 자식 노드 키값보다 크거나 같음 -> 루트 노드가 가장 큼, 값이 큰 데이터가 우선순위를 가짐

min heap: 값이 작은 원소부터 추출 / 부모 노드의 키 값이 자식 노드의 키값보다 항상 작거나 같은 -> 루트 노드가 가장 작음, 값이 작은 데이터가 우선순위를 가짐

heapify: 힙에서 특정 노드와 그 하위 노드를 정렬하여 힙 속성을 유지하도록 만드는 과정
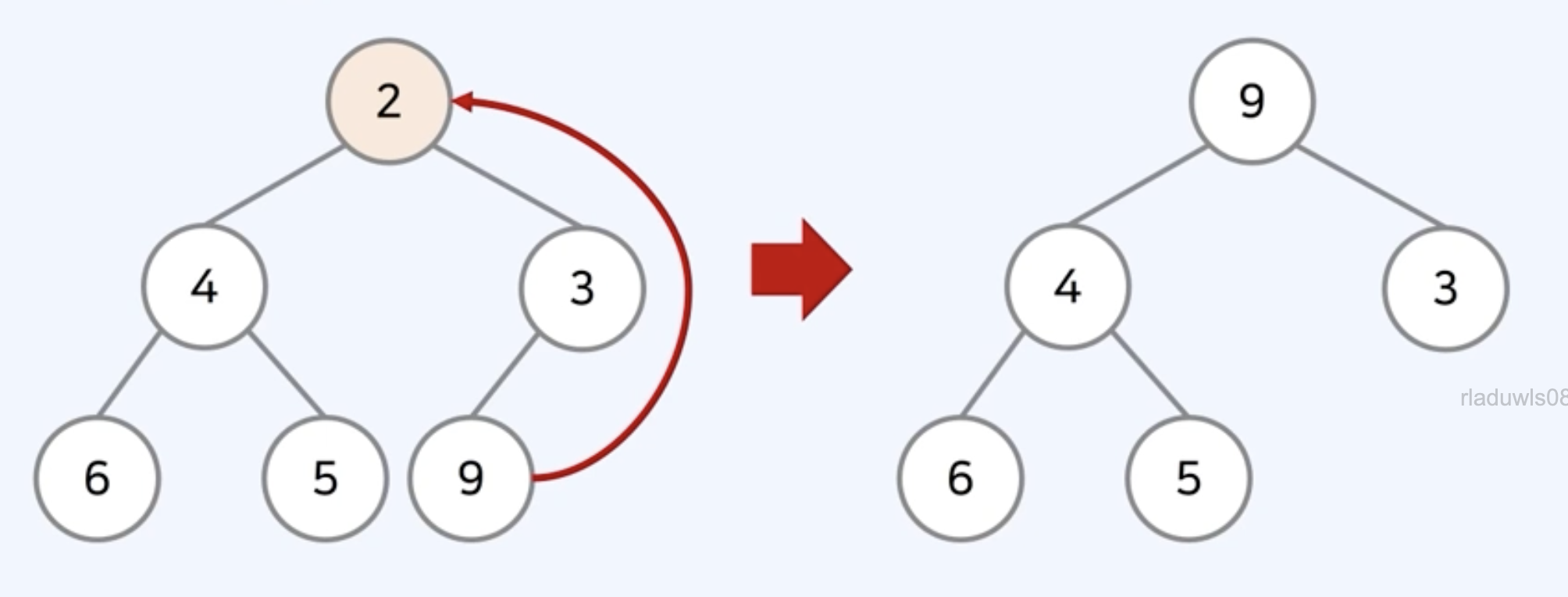
원소 삽입 - 상향식 힙 정렬 (Up-Heapify / Bubble-Up): 새 요소가 리프 노드에 추가되고 위로 올라가며 부모노드와 비교해 힙 속성 복구

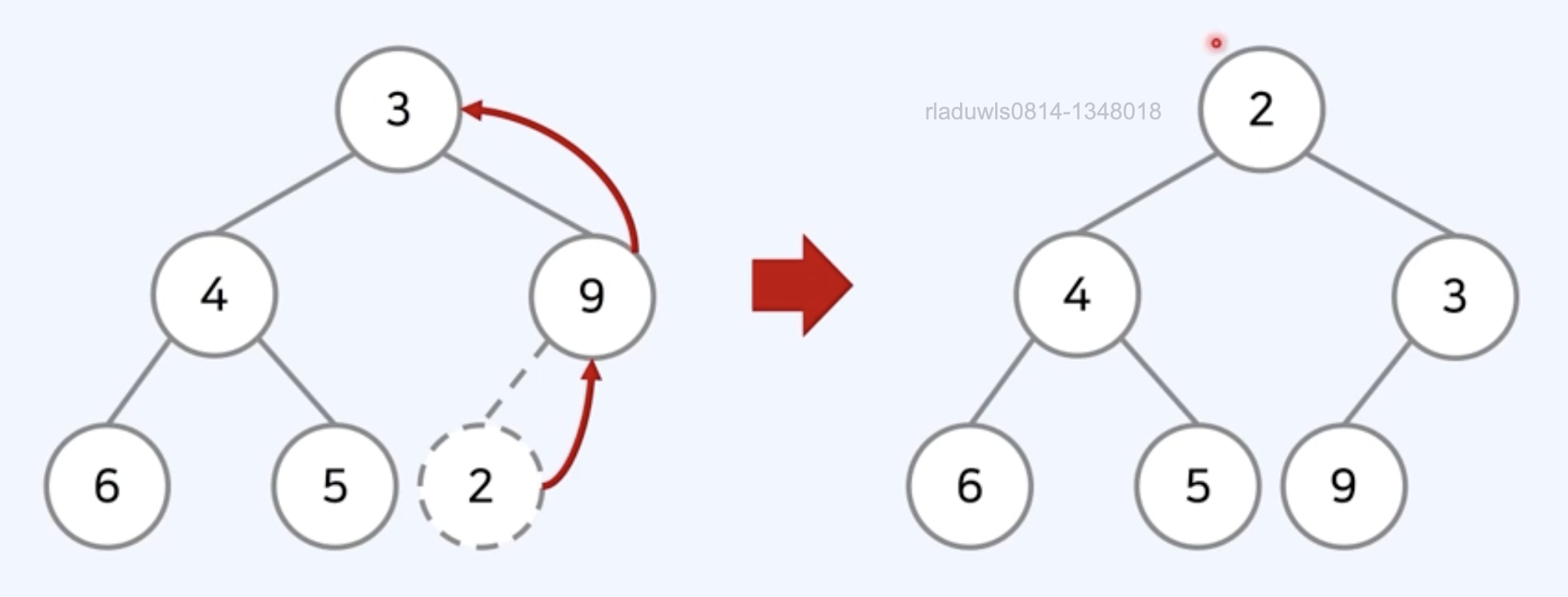
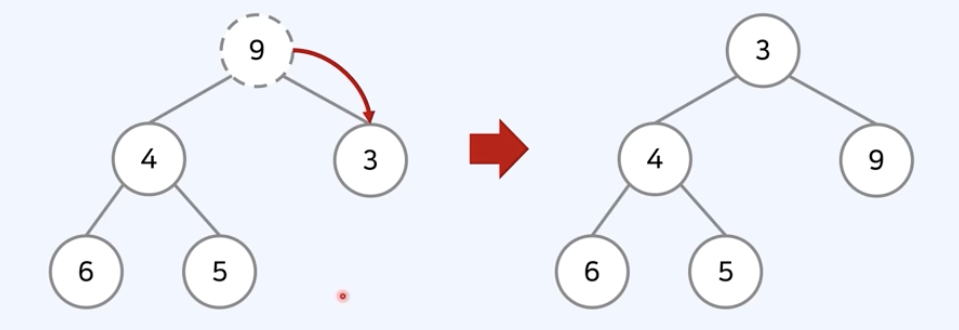
원소 삭제 - 하향식 힙 정렬 (Down-Heapify / Sink-Down): 마지막 노드가 루트 노드에 추가되고 아래로 내려가며 자식노드와 비교해 힙 속성 복구

완전 이진 트리에서 높이(h)와 노드수(N)는 다음과 같은 관계를 가짐

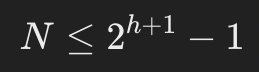
높이(h)는 노드 수(N)에 대해 다음과 같이 계산됨

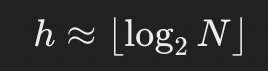
삽입과 삭제를 위한 최대 비교 횟수는 트리의 높이임. 즉 시간복잡도가 트리의 높이에 비례함 => 삽입,삭제에 대한 시간 복잡도는 O(logN)

단순한 N개의 데이터를 힙에 넣었다 모두 꺼내는 작업은 O(NlogN)

// 우선순위 큐를 배열로 구현
class PriorityQueue {
	constructor() {
		this.queue = [];
	}
	
	enqueue(element) {
		// 우선순위에 따라 데이터 삽입
		for (let i = 0; i < this.queue.length; i++) {
			if (this.queue[i] < element) {
				this.queue.splice(i, 0, element);
				return;
			}
		}
		// 큐에 자신보다 더 작은 값이 없으면 맨 마지막에 삽입
		this.queue.push(element);
	}
	
	dequeue() {
		return this.queue.shift();
	}
	
	front() {
		return this.queue[0];
	}
	
	size() {
		return this.queue.length;
	}
}

let pq = new PriorityQueue();

pq.enqueue(1);
pq.enqueue(2);
pq.enqueue(3);

console.log(pq); // PriorityQueue { queue: [ 3, 2, 1 ] }
console.log(pq.dequeue()); // 3
console.log(pq); // PriorityQueue { queue: [ 2, 1 ] }



// 우선순위 큐를 힙으로 구현
class PriorityQueue {
	constructor() {
		// 각 노드별 idx 접근을 쉽게하도록 1-based 인덱스를 만들기위해 초기값 0을 넣어줌
		this.queue = [0];
	}
	
	enqueue(element) {
		let insertIdx = this.queue.length;
		
		/* 
			부모 노드의 값이 현재 입력될 값보다 같거나 작으면
			부모 노드의 값을 insertIdx의 값에 넣어주고,
			insertIdx를 부모 노드의 idx로 바꾸고 다시 검사
			insertIdx === 1 인 경우는 이미 전체 탐색이 완료된 경우이므로 종료
		*/
		while (insertIdx > 1 && this.queue[Math.floor(insertIdx / 2)] <= element) {
			this.queue[insertIdx] = this.queue[Math.floor(insertIdx / 2)];
			insertIdx = Math.floor(insertIdx / 2);
		}
		
		this.queue[insertIdx] = element;
	}
	
	dequeue() {
		let delValue = this.queue[1];
		let lastValue = this.queue.pop();
		this.queue[1] = lastValue; // 리프 노드를 부모자리에 임시로 배치
		
		let qSize = this.queue.length - 1;
		let pIdx = 1; // 탐색을 시작할 부모 Idx
		let cIdx = 2; // 탐색을 시작할 자식 Idx
		
        /* 
			두 자식 중 큰 자식을 
			리프노드와 비교해 리프노드가 더 크면 정렬이 완료되었으므로 루프를 종료, 그때의 부모Idx 값이 리프노드
			부모 노드와 비교해 자식노드가 더 크면 부모와 자식을 바꾸고(값과 인덱스), 자식 Idx는 왼쪽 자식 Idx로 바꾸고 재검사
			
			cIdx > qSize 인 경우는 전체 탐색이 완료된 경우이므로 종료 
		*/
		while (cIdx <= qSize) {
			if (this.queue[cIdx] < this.queue[cIdx + 1]) {
				cIdx += 1;
			}
			
			if (lastValue >= this.queue[cIdx]) {
				break;
			}
			
			this.queue[pIdx] = this.queue[cIdx];
			pIdx = cIdx;
			cIdx *= 2;
		}
		
		this.queue[pIdx] = lastValue;
		
		return delValue;
	}
	
	front() {
		return this.queue[1];
	}
	
	size() {
		return this.queue.length - 1;
	}
	
	clear() {
		this.queue = [0];
	}
}

let pq = new PriorityQueue();

pq.enqueue(10);
pq.enqueue(5);
pq.enqueue(1);

console.log(pq); // PriorityQueue { queue: [ 0, 10, 5, 1 ] }
console.log(pq.dequeue()); // 10
console.log(pq); // PriorityQueue { queue: [ 0, 5, 1 ] }