[백준] 9613번 GCD 합 - Java, 자바

문제

https://www.acmicpc.net/problem/9613

코드

import java.io.*;

// 9613번 GCD 합
public class boj_1_9613 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));

        int t = Integer.parseInt(br.readLine());

        while (t-- > 0) {
            String[] inputs = br.readLine().split(" ");

            int n = Integer.parseInt(inputs[0]);

            int[] arr = new int[n];
            long answer = 0;

            for (int i = 0; i < arr.length; i++) {
                arr[i] = Integer.parseInt((inputs[i + 1]));
            }

            for (int i = 0; i < arr.length - 1; i++) {
                for (int j = i + 1; j < arr.length; j++) {
                    answer += gcd(arr[i], arr[j]);
                }
            }
            bw.write(answer + "\n");

        }
        bw.flush();
        bw.close();
    }

    public static int gcd(int a, int b) {
        while (b != 0) {
            int temp = b;
            b = a % b;
            a = temp;
        }
        return a;
    }

}

풀이

알아야 할 것

• GCD 구하는 법
• GCD를 더한 값의 범위(주어진 테스트케이스의 수를 보고 복잡도 생각해야함)

기본적으로 최대공약수를 구하는 방법을 알아야한다.
그리고 answer의 타입을 처음에 int로 하면 틀리게 되는데 그 이유는 테스트케이스의 값을 고려했을 때 int의 범위를 초과하므로 long 타입으로 지정해줘야한다. 왜 long을 해야하는지는 아래 자세하게 설명하겠다.

1. GCD 구하는 법
유클리드 호제법을 통해 최소공배수와 최대공약수를 구할 수 있다.

최대공약수란 어떤 두 수가 존재할 때 공통인 약수 중 가장 큰수
(최대공배수란 어떤 두 수가 존재할 때 그들의 배수가 되는 가장 작은 수)

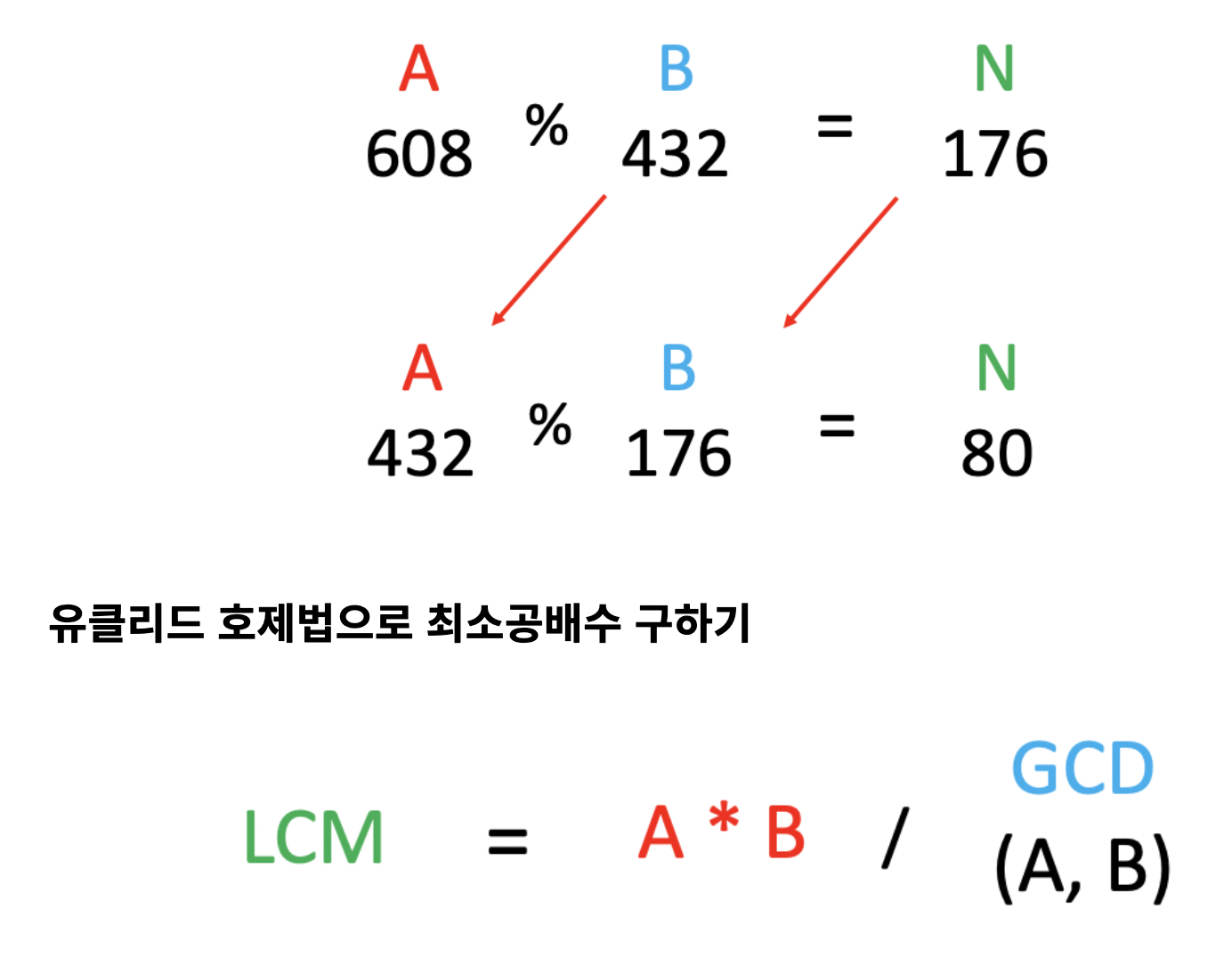
유클리드 호제법의 핵심은 모듈러 연산이다. 모듈러 연산을 반복하여 0이 될 때까지 간다면 최대공약수를 구할 수 있다.

1. A와 B 중 더 큰 수 찾기
2. 큰수를 A로 작은수를 B로 설정
3. A % B = N 구하기
4. N == 0 이면 B는 최대 공약수
5. N != 0 이면 A = B, B = N 으로 대입하고 3~5번 반복
   

2. GCD를 더한 값의 범위
테스트케이스의 수(n)가 1~100이고, 입력으로 주어지는 수 1~1,000,000이다.
n개의 수를 2개씩 짝지어 만드는 모든 경우의 수는 n(n-1)/2이므로 , 100*99/2=4950인데 만약 각각 n이 1,000,000이라면 총 합의 최대 범위는 49억이 된다.

int의 범위는 약 21억까지이고 49억은 int의 범위를 초과하므로 long으로 바꿔줘야한다.

참고
https://wonit.tistory.com/411
https://binghedev.tistory.com/59
http://tcpschool.com/java/java_datatype_basic