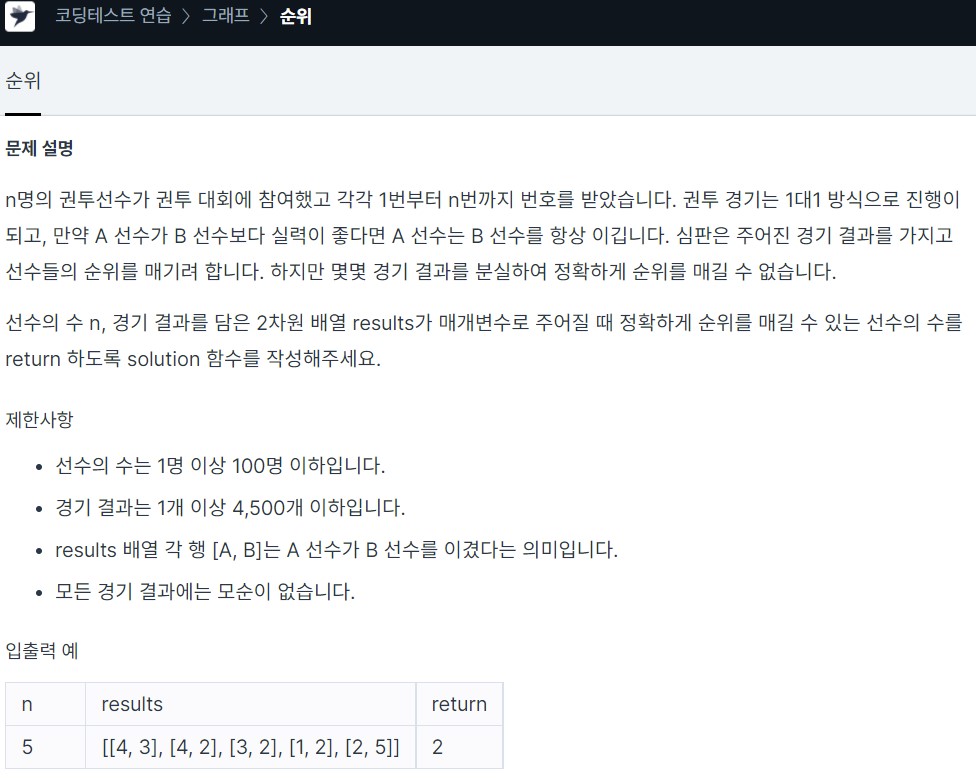
Lv3. 순위
💡Summary & Idea
result 배열 각 행 [a,b]는 a가 b를 이겼다는 의미이다- 처음 각 선수간 순위가 있으니
위상정렬(Topological Sort)로 구현해야 하나 생각을 했다 (indegree와 outdegree의 차수를 더한 값이 n-1이 되면 모든 선수들과 관계를 알 수 있으니 순위를 알 수 있지 않을까 했지만, 그렇지 않은 관계도 있었다)
- 그래서 사용해야 하는 것이 모든 정점 쌍에 대해 둘 사이의 최단 거리를 찾는 플로이드 와샬 알고리즘을 사용한다
📜Floyd Warshall Algorithm
- 모든 정점 간 최단 거리를 구할 때 사용
- 정점 집합
S에서 u에서 v로 가는 최단 경로의 길이를 D(u,v)라 할 때
① 경로가 k를 경유하지 않는다: S-{k}에 포함된 정점들만을 경유점으로 사용
② 경로가 k를 경유한다: D(u,k)와 D(k,v)로 경로를 나눌 수 있다
경유
③ 경유 지점 k는 정점 집합 S의 모든 값이 될 수 있다
④ D(u,v)=min(D(u,v), D(u,k)+D(k,v))로 나타낼 수 있다
int V //정점의 개수
int adj[MAX_V][MAX_V]
// adj[u][v]=u에서 v로 가는 간선의 가중치
int via[MAX_V][MAX_V]
//via[u][v]=u에서 v까지 가는 최단 경로가 경유하는 점 중 가장 번호가 큰 정점
void floyd () {
for (int i=0; i<V; i++) adj[i][j]=0;
memset (via, -1, sizeof(via));
for (int k=0; k<V; k++) {
for (int i=0; i<V; i++) {
for (int j=0; j<V; j++) {
if (adj[i][j]>adj[i][k]+adj[k][j]) {
via[i][j]=k;
adj[i][j]=adj[i][k]+adj[k][j];
}
}
}
}
}
void reconstruct (int u, int v, vector<int> &path) {
if (via[u][v]==-1)
path.push_back(u);
if (u!=v) path.push_back(v);
}
else {
int w=via[u][v];
reconstrcut (u,w,path);
path.pop_back(); //w가 중복으로 들어가므로 지움
reconstruct (w,v,path);
}
}
✏️Solution
vector<vector<bool>> adj에서 adj[u][v]=true 라는 뜻은 u가 v를 이긴다는 뜻이다- u가 k를 이기고 k가 v를 이기면 u가 v를 이기는 것과 같다
즉 adj[u][k]==true && adj[k][v]==true 이면 adj[u][v]=true
adj를 조사해서 각 정점에서 경기 결과를 알 수 있는 경우가 n-1이면 모든 선수와 승/패를 판단할 수 있다는 뜻이므로 순위를 매길 수 있다는 뜻이다
✏️Source Code
#include <string>
#include <vector>
using namespace std;
int solution(int n, vector<vector<int>> results) {
int answer = 0;
vector<vector<bool>> adj(n+1, vector<bool> (n+1, false));
for (int i=0; i<results.size(); i++)
adj[results[i][0]][results[i][1]]=true;
for (int k=1; k<=n; k++) {
for (int i=1; i<=n; i++) {
for (int j=1; j<=n; j++) {
if (i==j) continue;
if (adj[i][k] && adj[k][j])
adj[i][j]=true;
}
}
}
for (int i=1; i<=n; i++) {
int cnt=0;
for (int j=1; j<=n; j++) {
if (i==j) continue;
if (adj[i][j] || adj[j][i]) cnt++;
}
if (cnt==n-1) answer++;
}
return answer;
}