Algospot
1.<종만북> 08. 동적계획법_폴리오미노 (polyomino) c++

구하고자 하는 것은 세로 단조 폴리오미노이다. 세로 단조 폴리오미노가 되려면 각 가로줄에 포함된 정사각형은 항상 일렬로 연속해 있다. 첫 줄에 i개의 정사각형이 속한 폴리오미노의 개수는 나머지 n-i개로 구성된 정사각형들로 폴리오미노를 만든 뒤, 이들을 적절히 맨 윗
2.<종만북> 08. 동적계획법_비대칭 타일링 (Asymmetric Tiling) c++

먼저 비대칭 타일링 문제를 풀기 위해서는 앞에서 공부했던 타일링 방법의 수 세는 알고리즘을 복습할 필요가 있다.2xn 사각형을 채우는 방법들은 맨 오른 쪽이 어떻게 채워져 있느냐로 나눌 수 있다. a는 마지막 타일의 가로길이가 1인 경우, b와 c는 마지막 타일의 가로
3.<종만북> 08. 동적계획법_삼각형 위의 최대 경로 개수 세기 (Tripath Count) c++

먼저 삼각형 위의 최대 경로 갯수를 세기 위해서는 최대 경로를 푸는 알고리즘을 먼저 짜야한다. (y,x) 의 위치에서 바로 아래 숫자 혹은 오른쪽 아래 숫자로 내려갈 수 있기 때문에 (y+1, x)와 (y+1, x+1) 중에 큰 숫자를 찾아 더해서 내려가면 된다.
4.<종만북> 08. 동적계획법_외발 뛰기 (Jumpgame)
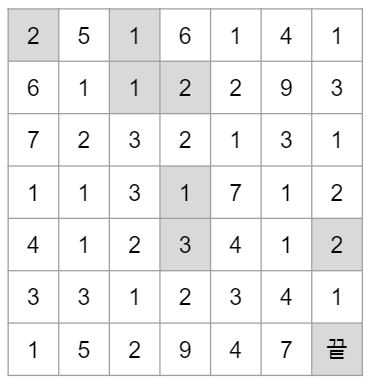
밑에 그림처럼 n x n 크기의 격자에 1부터 9까지 정수를 쓴 게임판이 있다. 이 게임의 목적은 게임판의 왼쪽 위 칸에서 시작해 게임파의 맨 오른쪽 아래 칸에 도착하는 것이다. 각 칸에 적혀 있는 숫자만큼 아래쪽이나 오른쪽으로 이동할 수 있다.코드 8.4기저사례: 게
5.<종만북> 08. 동적계획법_합친 LIS (JLIS, Joined Longest Increasing Subsequence
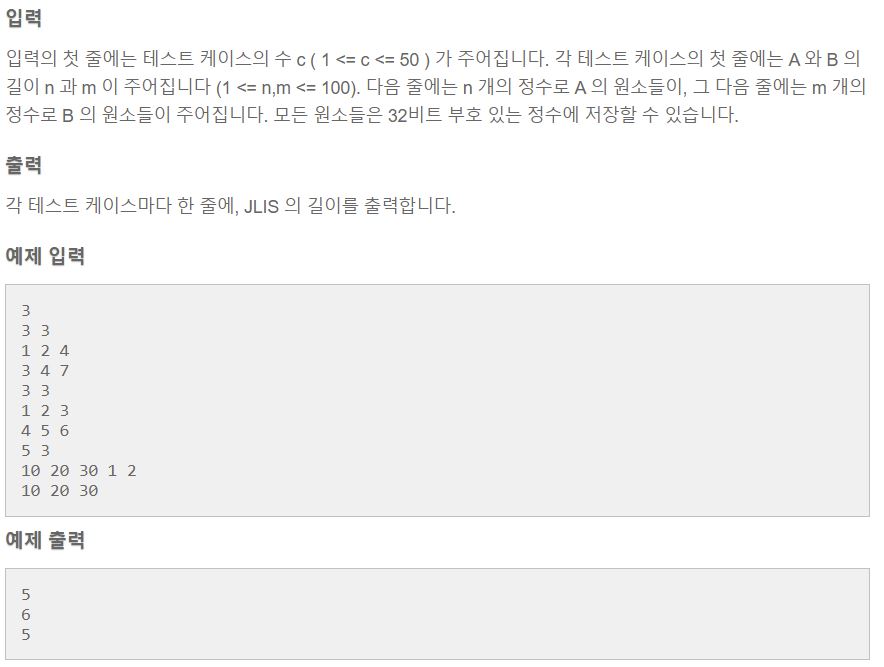
앞에서 LIS 문제는 많이 다뤘다. 하지만 이번에 다룰 내용은 더 심화된 JLIS 문제이다. 근데 책에서는 난이도가 하 라고 되어있다..하하..예를 들어 '1 3 4 7 9'은 '1 9 4'와 '3 4 7'의 JLIS이다. 문제는 정수 수열 A, B가 주어질 때 JLI
6.<종만북> 08. 동적계획법_우물을 기어오르는 달팽이 c++
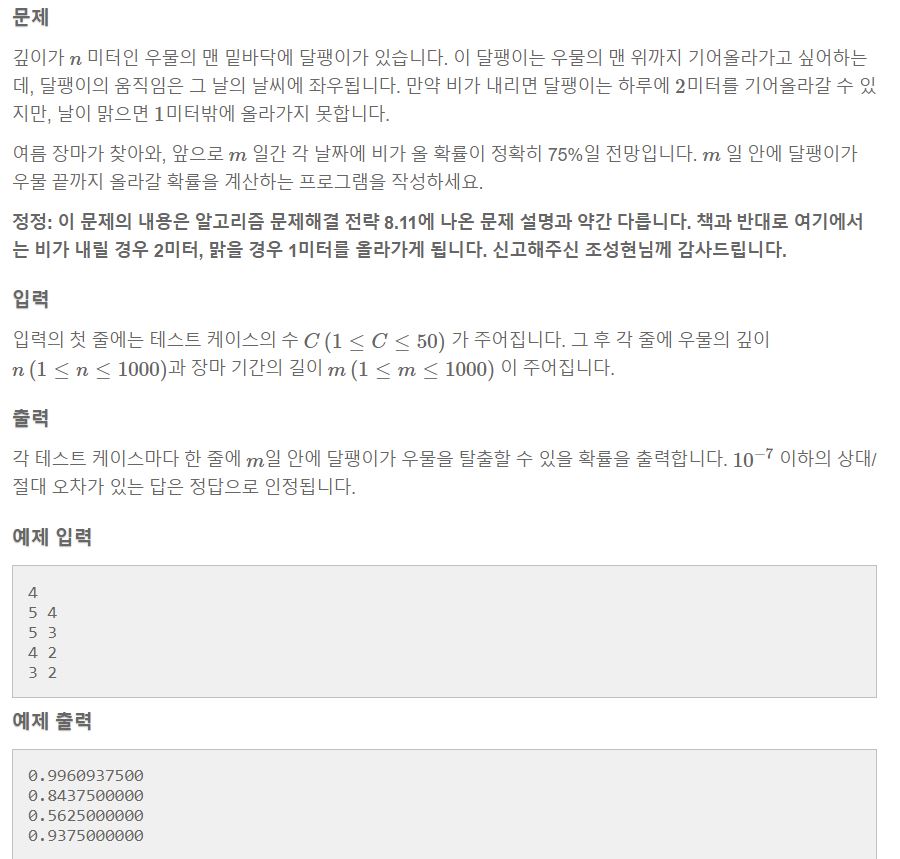
확률과 경우의 수는 밀접한 관련이 있기 때문에 많은 경우 확률을 계산하는 문제에도 동적 계획법을 써먹을 수 있다. 먼저 책의 예제에서 각 날짜에 비가 올 확률이 정확히 50%라고 가정할 때, m일 안에 달팽이가 우물 끝까지 올라갈 확률을 먼저 본다. m일 간 비가
7.<종만북> 28. DFS_위상정렬 (TopologicalSort) c++

앞에서 했던 위상정렬이 inDegree 즉, 진입차수의 개수를 이용하여 풀었다면 이번에는 조금 다른 방법으로 접근한다.visited 함수를 두어 모든 정점들을 방문하고, 각 정점에서 간선으로 연결된 다음 정점을 방문하며 order에 기록해둔다.모든 순회가 끝나고 나면