Greedy Method

Method (1)

탐욕적인 (욕심쟁이) 알고리즘 : 결정을 해야 할 때마다 가장 좋다고 생각되는 것을 선택함

• 최적화 문제(가능한 해들 중 가장 좋은 해를 찾는 문제)를 해결할 수 있음
• 데이터 간 관계 고려를 하지 않고, 가장 좋은 값을 선택함. 선택을 번복하지도 않음

선택한 데이터를 버리고 다른 것을 취하지 않음

Method (2)

• 그 당시, local에는 최적임. local을 모아 global을 만들었다고 해서, 궁극적인 최적이 된다는 보장이 없음.

탐욕적인 알고리즘은 최적의 해답을 주는지를 반드시 검증해야 한다.

Method(3)

1. 선정 과정(selection procedure)
   현재 상태에서 가장 좋으리라고 생각되는 가능한 해답을 찾음
2. 적정성 점검 (feasibility check)
   새로 얻은 해답모음이 적절한지를 결정함
   적절하다면, solution set에 포함시킴
3. 해답 점검 (solution check)
   새로 얻은 해답모음이 최적의 해인지를 결정함

Procedure Greedy Code

/* A(1...n) contains the n inputs * /
solution = null
for i to n do
	x = SELECT (A)
    if FEASIBLE (solution,x)
		then solution=solution U {x}
	endif
endfor
return(solution)

예제: 거스름돈 문제

현재 유통되는 동전 + 그리디 알고리즘 -> 그리디 알고리즘이 최적임을 알 수 있음

최적의 해를 얻지 못할 수도 있다고?

11원짜리 동전이 생겨났다고 쳤을 때, 거스름돈의 액수가 15원이라면
11*1, 1*4 => 총 동전은 5개
10*1, 5*1 => 총 동전은 2개
다음과 같이 optimal이 아닌 현상이 발생함을 알 수 있음

Fractional Knapsack Problem

n개의 물건과 1개의 배낭(knapsack)이 있다.
각 물건 i의 무게는 wi, 값어치는 Pi이며, 배낭의 용량은 무게 M까지 가능하다.
물건 i를 xi(0<=xi<=1) 만큼 배낭에 넣는다면 이윤은 Pi * xi가 된다.
물건들을 배낭에 섞어서 넣되, 무게가 M을 넘지않으면서 이윤은 최대가 되도록 어떻게 배낭에 물건들을 넣으면 될까?

해결해 봅시다

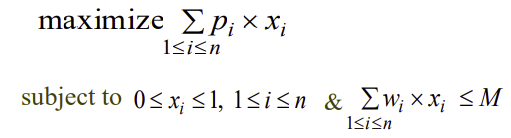
1. Start with an arbitrary one
2. Start with the largest profit
3. Start with the smallest weight
4. 단위 무게 당 profit이 큰 것

4가지 경우를 모두 실습해 보고, 가장 optimal한 것을 골라 봅시다.

실습을 통해 4번이 가장 optimal 한 것을 알 수 있음

시간복잡도 구하기

정렬이 된 경우 O(n), 정렬이 되지 않은 경우 O(nlogn)이 되는 것을 알 수 있음.

Code

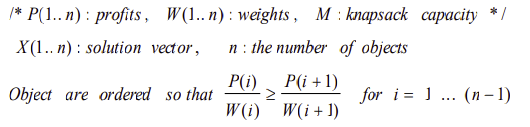
X=null; Cu=M;
for i=1 to n
	if (W(i)>Cu) then exit;
    X(i)=1;
    Cu=Cu-W(i);
endfor
if(i<=n) then X(i) = Cu/W(i)
end

0-1 Knapsack Problem

방법 1 : 무작정 알고리즘

n개의 물건에 대해서 모든 부분집합을 다 고려함
크기가 n인 집합의 부분집합의 수는 2^n개, 너무 많음

방법 2 : 가장 비싼 물건부터

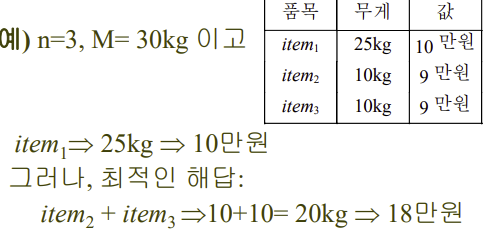
방법 3 : 무게 당 가치가 높은 물건부터

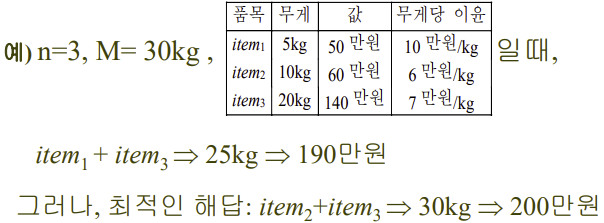
결론?

이러한 문제에는 Greedy보다 더 적합한 알고리즘이 존재함

응용 분야

• 조합론, 계산 이론, 암호학, 응용수학 분야 기본적인 문제
• '버리는 부분 최소화시키는' 원자재 자르기
• 자산투자 및 금융 포트폴리오
• Merkle-Hellman 배낭 암호 시스템의 키 생성

Two-Way Optimal Merge Patterns

Recall : 각각 n, m개의 레코드를 가진 정렬된 두 개의 파일을 합병하는 걸리는 시간은 O(n+m) 이다

문제 : 주어진 2개 이상의 정렬된 파일들을 하나의 정렬된 파일로 합병하고자 한다. 단, 비교(comparison)회수를 최소로 하도록 한다.

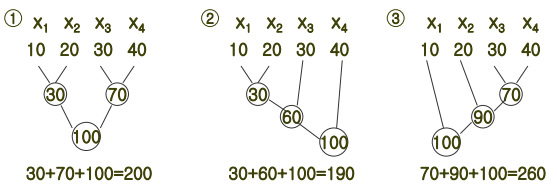
F=(20,30,10,5,30)일 때, Merge Pattern을 Tree 모양으로 재정렬해 보자.

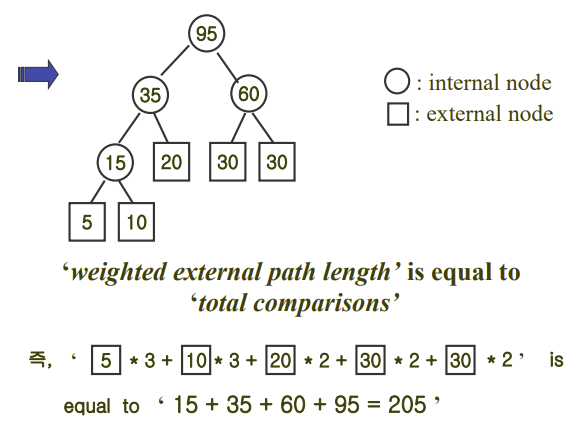
가장 최적화된 해는 다음과 같으며, 각 노드의 깊이 * 각 노드의 값을 모두 더한 것은 총 비교 회수가 되는 것을 알 수 있음

시간복잡도 분석

Huffman Code

Optimal binary tree with minimum weighted external path length의 또 다른 응용

Prefix Code

원소가 이진수인 집합으로, 집합에 있는 어떤 수도 다른 수의 prefix가 아닌 수로 이루어진 것

ex)
{00, 01, 100, 1010, 110} == Prefix
{10, 01, 0110} != Prefix

Why Prefix?

Huffman with Prefix

문제 : 6개의 문자 a1,a2, … a6의 빈도는 다음과 같다.
a1은 25%, a2은 20%, a3은 20%, a4은 10%, a5은 10%, a6은 15%이다.
각 문자에 이진수를 할당하여 prefix code가 되도록 디자인하되, 6개의 문자를 사용하여 코드 메시지를 보낼때 전체 길이가 최소가 되도록 디자인하시오.

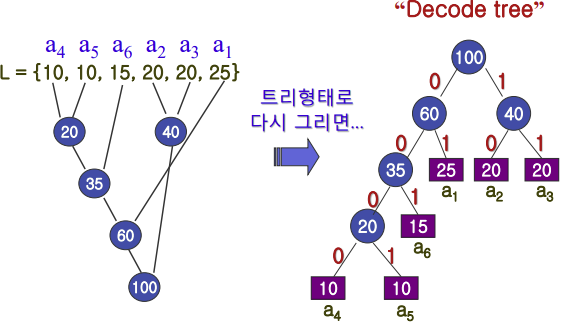
Huffman Example

4가지 문자 a, p, l, e에 대한 prefix 코드를 구하여라

문자는 4개이므로 최대 digit의 수는 3개여야 함.
가능한 예 :
a:0, p:10, l:110, e:111
a:11, p:0, l:100, e:101
다음과 같은 다양한 예가 나올 수 있으나, 상단의 Huffman 알고리즘을 사용하여 가장 효율적인 Prefix를 디자인할 수 있음