처음배우는 컴퓨터구조 - MIPS(1)

본 시리즈은 비전공자가 공부한 computer science, 그중에서도 컴퓨터구조를 정리한 글입니다. 틀린내용이 있다면 댓글로 알려주시면 정말정말 감사하겠습니다. 참고한 책은 Computer Organization and Design MIPS Edition입니다

Signed Binary Subtraction

저번시간 마지막에 우리는 정수의 뺄셈은 2의보수표현 + 덧셈으로 표현이 가능하다고 배웠다 예시를 한가지 들어보면

위와같은 수식이 있다고 가정해보죠. 7-6을 표현한 수식인데 -6을 2의보수로표현하면 두번째줄처럼 표현이 되고 7과 더하기 operation을 실행하면 bitwise연산을 통해 아래와같은 값이 나오게됩니다. 근데 우리가 배웠던것중에 정수는 4byte 즉 32bit로 표현해야하는데 결과를보면 맨앞에 1이라는게 올림으로 인해 생기게되고 이는 33bit를 표현하는 수가 됩니다. 이런경우엔 어떻게되냐면 간단하게 없애면됩니다 그래서 1이라는 답이 나오게되는거죠.

정수의 뺄셈을 요약을 해보면 아래와 같다라고 생각하면 됩니다.

1. a-b = a+(-b)로 계산한다
2. b를 양수/음수 관계없이 -b(2의 보수 표현)로 만들어서 덧셈을 한다

예를 들어 a-2라는 수식이 있다고 하면 a-b형태일때 2는 b가되겠죠 그러니까 1번규칙처럼 b에 -를 붙여서 a+(-b)로 계산하면 된다는건데 사실 이 설명을 들으면 더 헷갈릴수있으니 살짝 지워놓겠습니다... 어디까지나 보편적인 규칙이라는거니까요

---

Overflow

2147483647-(-2)연산의 결과를 이진수로 나타내면 어떻게될까요?
2147483647은 양수로표현할수있는 32bit의 가장 큰값이기때문에 signbit가 0이고 나머지는 1이겠죠. 그리고 (-2)가 b이기때문에 마이너스를 붙여 2로바꾸고 -를 +연산으로 바꿔주면 최종적으로
2147483647+2라는 연산이 됩니다. 이를 이진수연산을 해봅시다

결과를 해석해볼까요 우린 우선 signed bit라고 해석을 했기때문에 결과도 signed bit라고 해석을 해보면 우선 절댓값은 모르겠는데 sign bit가 1이니까 결과가 음수라는걸 알수있습니다. 음...?

뭔가 이상하죠. 양수-(음수)는 절댓값을 몰라도 양수가 되어야한다는 사실은 아마 다들 아실겁니다. 우선 이상한 부분은 잠시 접어두고 sign bit가 1이니까 2의 보수표현을 통해서 10진수로 바꿔보면 결과는 -2147483647이라는 값이 나오게됩니다. 아마 처음 저 수식을 보고 모든분들이 2147483649라는 결과가 나올거라고 예상하셨을텐데요 절댓값도 부호도 전부 다른 값이 나오게됩니다.

왜그럴까를 생각해보면 sign value라고 가정했을때 표현할수있는 최댓값은 2147483647인데 실제로 2를 더하면 2147483649라는 값은 나오지만 표현이 불가능하기때문에 이런 결과가 나오는거라고 할 수 있습니다. 그리고 이런 현상을 우리는 overflow라고 합니다

여기서 한가지 더 개념을 배워가면 우리는 sign bit만 가지고 overflow가 일어나는지 일어나지 않는지 알 수가 있습니다

더하기 연산 => 부호가 같은 operand를 가지고 연산을 하면 overflow가 발생할 수 있음
빼기 연산 => 부호가 다른 operand를 가지고 연산을 하면 overflow가 발생할 수 있음

---

Unsigned Add/Sub

그렇다면 이런질문이 생길수도있죠

overflow는 필연적인건가요? 다른 방법은 없나요?

결론부터 말하면 MIPS Instruction에 unsigned instruction이 있습니다 그중에서도 unsigned add와 unsigned sub가 있고 이를 addu, subu, addiu라고 표현합니다. MIPS의 unsigned 명령어의 의미는 정확하게는 연산의 결과, overflow가 발생해도 exception이 발생하지 않는다입니다. 그러면 어떻게 이 연산이 exception을 발생시키지 않는지를 이야기해보겠습니다.

0111 1111 1111 1111 1111 1111 1111 1111 이라는 이진수는 2147483647라는 값을 가지고 있고 32bit에서 signed로 표현할 수 있는 최대의 크기라고 이야기한적이 있습니다.(좀전에요) 만약에
0111 1111 1111 1111 1111 1111 1111 1111와 0111 1111 1111 1111 1111 1111 1111 1111를 더한다면 이 두가지 operand가 signed라고 가정하면 당연히 overflow가 발생하겠지만 만약에 두 operand를 unsigned라고 해석하고 연산을 한다면 1000 0000 0000 0000 0000 0000 0000 0000 이라는 값을 42억 어쩌구저쩌구라고 표현할 수 있게됩니다. 맨앞 bit가 sign을 의미하는게아니라 2의 32제곱을 나타내는 자리가 되니까요 그래서 이런경우엔 unsigned Instrution을 사용하면 됩니다

여기서 주의해야할점이 있다면

addu $t3, $t1, $t1

라는 assembly text가 있을때 t1 register에 있는 값과 t1 register에 있는 값을 더해서 그 연산결과를 t3 register에 저장한다라고 해석할 수 있는데 여기서 unsigned로 해석하는 부분은 연산의 결과뿐이지 unsigned연산이니까 register에 있는 값을 unsigned로 해석하면 안된다는 부분은 주의를 하셔야합니다.

🔥 궁금한점: addu는 operand의 값들을 unsigned로 보는것인가? 아니면 결과를 unsigned로 보는것인가

• 내생각1: 만약에 register에 있는 값들을 signed로 보면 결과가 음수여야하는데 양수로 봐야하는 문제
• 내생각2: 만약에 register에 1111 1111 1111 1111 1111 1111 1111 1111를 넣어서 양수와 더하면 overflow가 발생

✅ operand값이랑 destination register의 값들을 모두 unsigned취급

정수의 곱셈, 나눗셈

MIPS IntegerMultiplication

가장먼저 정수의 곱셈을 MIPS Instrution으로 표현하면

mult rs, rt
multu rs, rt

이렇게 두가지로 표현할 수 있습니다. 지금까지 봤던 text와 다른부분이 있다면 destination register가 명시되어있지 않은건데 곱셈연산의 결과는 두개의 32bit register에 나눠져 들어가게 된다(자동으로) 그래서 우리가 곱셈 연산의 결과를 사용하기 위해서는 자동으로 저장된 register의 값을 저장해야합니다. 참고로 여기서 multu의 경우 operand가 모두 양수라고 가정합니다.

우선 곰셉의 결과는 HI라는 register와 LO라는 register에 나눠서 저장하게 된다. 예를 들어서 2X3의 경우엔 HI에는 0 LO에는 6이라는 값이 저장되게되는거죠.

그리고 해당 값을 사용하기 위해 아래 두가지 Instruction을 사용해야하는데

mfhi rd
mflo rd

이 두가지에 destination register가 있기때문에 곱셈 Instruction의 경우 또하나의 text로 destination register를 지정해줄수있다고 이해하고 있으면 편하더라고요

🔥 궁금한점: 무슨기준으로 LO와 HI에다가 저장하는걸까...?

• 내생각1: 32bit의 최댓값을 넘지 않으면 LO 넘으면 HI?

✅ lui와 ori두개로 표현하는방식처럼(실제로 이방식은 아님)

MIPS Integer Division

정수의 나눗셈을 MIPS Instruction으로 표현하면

div rs, rt
divu rs, rt

이렇게 두가지로 표현할 수 있고 이 연산역시 결과가 HI LO에 저장되는데 곱셈과 다른점이 있다면 HI에는 나머지가 LO에는 몫이 저장된다는 점입니다. 그러니까 mflo는 register(destination)에 몫을 저장하고 mfhi는 register에 나머지를 저장할 수 있습니다.

궁금한점이 한가지 있었는데 divu를 쓸때는 결과를 unsigned로 보는걸까 아니면 operand를 unsigned로 보는걸까 구글링을해보니까 stackoverflow에 아래와같은 답변이 있는데 결과를 unsigned로 보기보다는 각각의 operand를 unsigned로 보고 연산을 수행한다고 합니다.

---

Logical Operations(논리연산)

Or, And

MIPS에서의 Logical Operation에는 아래와같은 연산이 존재하고

AND, OR, NOR, AND immediate, OR immediate, shift left logical, shift right logical

그리고 각각의 연산은 같은 자리수끼리 연산하는 bit wise연산을 수행합니다

이중에서 or과 and에 관한 한가지 예시만 간단하게 들어보면 위의 예시는 아래와같은 assemble text의 연산결과인데요

or $t0, $t1, $t2

해당 연산은 위의 사진처럼 각각의 자리수끼리 or연산을 한 결과를 나열해주면 됩니다. 만약에 and연산이었다고 하면 연산의 결과가 바뀌겠네요

or 연산 : A or 0 = A
and 연산 : A and 1 = A

nor

nor은 not or의 줄임말입니다. 순서대로 not을 하고 or을 하는게 아니라 or연산을 하고 그 연산의 결과에다가 not을 하는 연산입니다. 아주 간단한 연산이니 예시를 하나만 보고 넘어가죠

t1과 t2의 or연산의 결과는 result인데 여기다가not을 해준연산의 결과를 t7에다가 저장해준 연산입니다. nor연산이 중요한 이유는 nor을 통해 not을 표현할 수 있기때문입니다.

not A는 not (A or A)이고 A or A는 A이기때문에 A or 0과 같습니다. 즉, 결론을 정리해보면

not(A)
= not(AorA) == A nor A
= (not(Aor0) == A nor 0)

이라고 정리할 수있는거고 assembler text로 notA를 표현해보면 아래와 같이 표현이 가능합니다.

nor $t8, $t1, $t1 혹은 nor $t8, $t1, $zero

sll, srl

이건 사실 기계공학 마이컨할때 배웠던 내용이어서 sll이랑 srl이라는 용어에만 익숙해지면 되는 부분이었던거같아요. sll은 shift left logical이고 srl은 shift right logical입니다. 이게 뭐지라고 생각하실수 있는데 32bit를 옆으로 옮기는 연산입니다.

되게 간단한데 예를들어서 간단한 8bit값이 0011 0100이 있다고 했을때 왼쪽으로 두칸 움직이면 1101 0000이 됩니다. 맨왼쪽 00이 넘어가서 사라지고 비어잇는 부분이 0으로 채워집니다. 사실 오른쪽도 똑같습니다. 오른쪽으로 두칸 움직이면 0000 1101이 되겠네요.

해당 연산의 의미?라고 하면 왼쪽으로 i bit shift하는 것은 2의 i제곱을 곱하는 것과 같은데 연산속도는 곱셈보다 빠르다는 장점과 의미를 가지고 있습니다. 오른쪽으로 i bit shift하는것은 2의 i제곱을 나누는것과 같을거고 연산속도는 당연히 나눗셈보다는 빠르다고합니다.

✅ logical 연산이기때문에 unsign extension(zero extension)이라서 빈자리를 0으로 채우는거임

---

Representing Instructions in Computer

지금까지 공부한 내용은 Assembly text를 해석하는 방법?에 관한 내용이었습니다. 우리가 code로 쓰는 연산이 어떻게 작동하는지를 배웠다면 이번에 공부해볼 내용은 이런 명령을 어떻게 binary명령으로 바꿀수있을까에 대한 내용입니다. 즉 컴퓨터에게 이진수로 명령하는 방법을 배웁니다 실제로 우리가 명령할일은 없지만요

공부했던 모든 내용은 MIPS기반이었기때문에 계속해서 MIPS를 기반으로 이야기를 이어나가보겠습니다. MIPS에서 assembly text를 이진화된 Instruction으로 표현하는 표현방식에는 크게 3가지가 있습니다. R-format, I-format, J-format입니다. 그중에서 가장먼저 R-format에 대해 배워보겠습니다

format이라는 용어가 익숙하지 않을수있는데 사실 그냥 편하게 생각하면 공식이라고 생각하면 편합니다. 미리 스포를 조금 하자면 add는 어떤 영역에 어떤 이진수를 넣어주면되고 addi는 어떤영역에 어떤 이진수를 넣어주면돼라는거에서 어떤 영역이 규칙으로 정해져있는것이니 받아들이면되는거라 크게 겁먹을 필요는 없습니다

R-format

가장 먼저 R-format입니다. 생김새를 먼저 보겠습니다.

이렇게 생긴 format(제가생각했을땐 규칙정도로 생각하면 편하더라고요)인데요. 각각의 field를 간단하게 소개하자면

Instruction fields
■ op: operation code (opcode)
■ rs: first source register number
■ rt: second source register number
■ rd: destination register number
■ shamt: shift amount (00000 for now)
■ funct: function code (extends opcode)

우선 op는 뭐냐면 operation code인데 연산자마다 정해져있습니다... 뭐라설명하기가 애매하네요... 표를보면 이해를 하실수있으니 그냥 넘어갑시다 그리고 뭐 rs는 첫번째 register number이고 rt는 두번째 register를 가리킨다고하네요. shamt는 우리 logical할때 sll srl할때 썼던 shift constant입니다. funct는 function code인데 이것도 표를 보면 알수있으니까 넘어가겠습니다

중요한 부분은 각각의 field에 bit가 정해져있다는겁니다, 지금부터 R-format의 대표적인 Instruction인 add를 보도록 하겠습니다.

add $t0, $s1, $s2

라는 assembly text가 있다고 합시다. 우린 add라는 operation을 통해 op와 funct를 채워줄수있습니다. 그리고 text에는 detination register가 먼저나오지만 R-format에서는 첫번째 operand register, 두번째 operand register, destination register순서대로 오기때문에 좀 헷갈릴수있지만 이렇게 만들어놨으니 이렇게 사용하면됩니다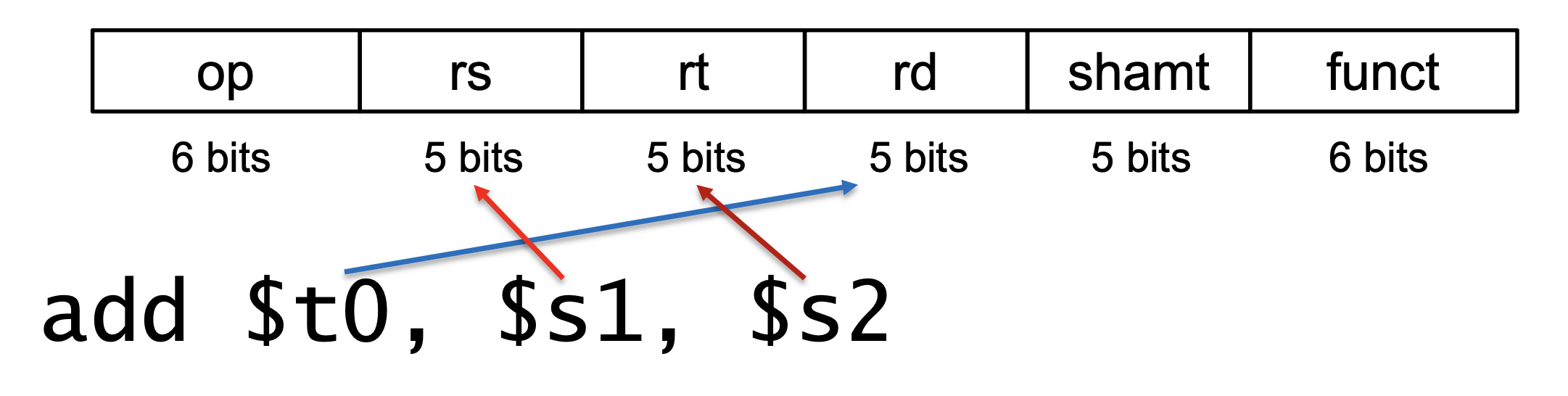

자그러면 add라는 operation의 op와 funct값을 알아봐야하는데 이를 알기위해서는 MIPS opcode map이 필요합니다

사진이 좀 작을 수 있지만 자세히 보면 add가 오른쪽에있는 빨간네모인데요 해당 table은 funct에 포함되어있고 add앞에 32라고 적혀있죠? 그러면 우리는 funct field에 32를 넣어주고 해당 funct table은 0번 op field에 연결되어있으니까 op에는 0을 넣어주면 되겠네요

근데 좀 이상한게 add같은경우는 funct table에 잇는데 addi는 op field에 있죠? 그러면 생각해볼수있는게 addi는 funct field가 필요없겠네?라는 생각을 해볼 수 있습니다. 그래서 addi같은 경우엔 funct field가 있는 R-format이 아닌 새로운 I-format의 규칙을 사용하게 됩니다. I-format은 우선 넘어가죠

그렇다면 우리는 add Instruction에서 op의 6bit에는 0을 넣어줘야하니 000000을 넣어주고 funct field인 6bit에는 32를 넣어줘야하니 100000를 넣어줘야합니다. 그리고 $t0는 8번 register이고 $s1은 17번 register $t1은 18번 register이기 때문에 각각의 5bit에는 register 번호를 적어주면 됩니다. 그런데 assembly text의 순서가 아닌 destination register가 마지막으로 와서 아래와 같은 순서로 5비트씩 register 번호를 넣어주면됩니다

$s1, $s2, $t0 => 17 18 8 => 10001 10010 01000

그리고 add연산은 shift constant가 필요없죠 logical Instruction이 아니니까요? 그러면 0으로 해주면됩니다. 5bit의 0이니까 00000이 되겠네요.

글로 쭉 풀어써서 되게 복잡해보이지만 최종적으로 R-format으로 해당 assembly text를 적어보면
000000 10001 10010 01000 00000 100000 이라고 할 수 있습니다.

근데 이를 16진수로 표현하려면 4bit씩 끊어야하기 때문에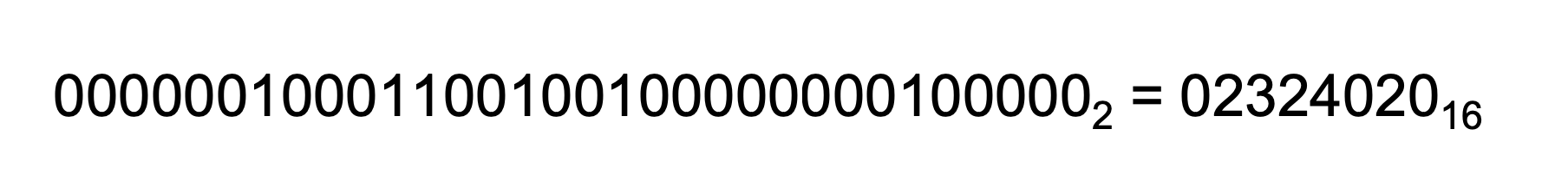

최종적으로는 위와같은 binary machine language로 Instrution을 표현해 컴퓨터에게 명령을 내리게됩니다.

최종적으로 정리해보면 위와같은 그림이 되겠네요
그러면 반대로 우리가 DisAssemble도 가능하겠죠? 예를들어서 0x016C6820이라는 Instruction이 있다고 하면 쭉 이진수로 풀어쓰면 0000 0001 0110 1100 0110 1000 0010 0000이 될거고 R-format이니까 6비트 5비트 5비트 5비트 5비트 6비트로 쪼개면 000000 01011 01100 01101 00000 100000이 되겠네요.

우선 op는 000000이니까 MIPS op map에서 funct field로 넘어가고 funct의 값이 100000인 32니까 add 연산인걸 알 수 있고 destination register은 01101이니까 13번이고 첫번째 operand register는 01011이니까 11번이고 두번째 operand는 01100이니까 12번이네요

최종적으로는 add $t5, $t3, $t4라는 text로 disassemble이 가능해집니다.

I-format

이번에는 I-format입니다. 이젠 대충 아 뭐 32비트를 R-format과 다른 field로 쪼갠녀석이겠구나라고 생각하실수도있고 그 생각이 맞습니다 그림을 먼저 보죠.

아까와는 다르게 rd가 없고 funct field가 없네요. 우리가 보통 I-format을 어느 연산자와 쓴다고 알고있으면 편하냐면 immediate arthmetic과 load/store instruction인데 load/store은 메모리주소관련내용이라 다음에 배워보고 우선 immediate arthmetic instruction 즉, 연산자에 i가붙는 녀석들은 I-format으로 표현한다고 생각하시면 편합니다.

실제 그림을 봐도 constant를 표현할 수 있는 16bit field가 존재하죠? 우리가 배웠던 ori, andi, addi를 I-format을 이용해서 표현할 수 있습니다

예를 한번 들어보죠 아래와같은 assembly text가 있다고 해봅시다

ori $11, $9, 0x8000

ori 연산자니까 I-format일거구요 우선 ori가 op가 13이기때문에 이진수로 표현하고 6bit로 표현하면 001101이 됩니다. 그리고 field에는 destination register가 없지만 맨위에 있는 rt가 rd의 역할을 한다고 생각하시면 됩니다. 그러면 첫번째 operand register는 9니까 5bit으로 표현하면 01001 destination register는 11이니까 5bit로 표현하면 01011이 됩니다 그리고 마지막으로 constant를 2진수로 바꾸면 1000 0000 0000 0000이 되고 연결하고 4비트로 쪼개면 0011 0101 0010 1011 1000 0000 0000 0000이 되고 16진수로 바꾸면 0x352B8000이라는 결과를 얻을 수 있습니다. 이번에도 글로써서 좀 복잡해 보일수있으니 그림으로 정리하면

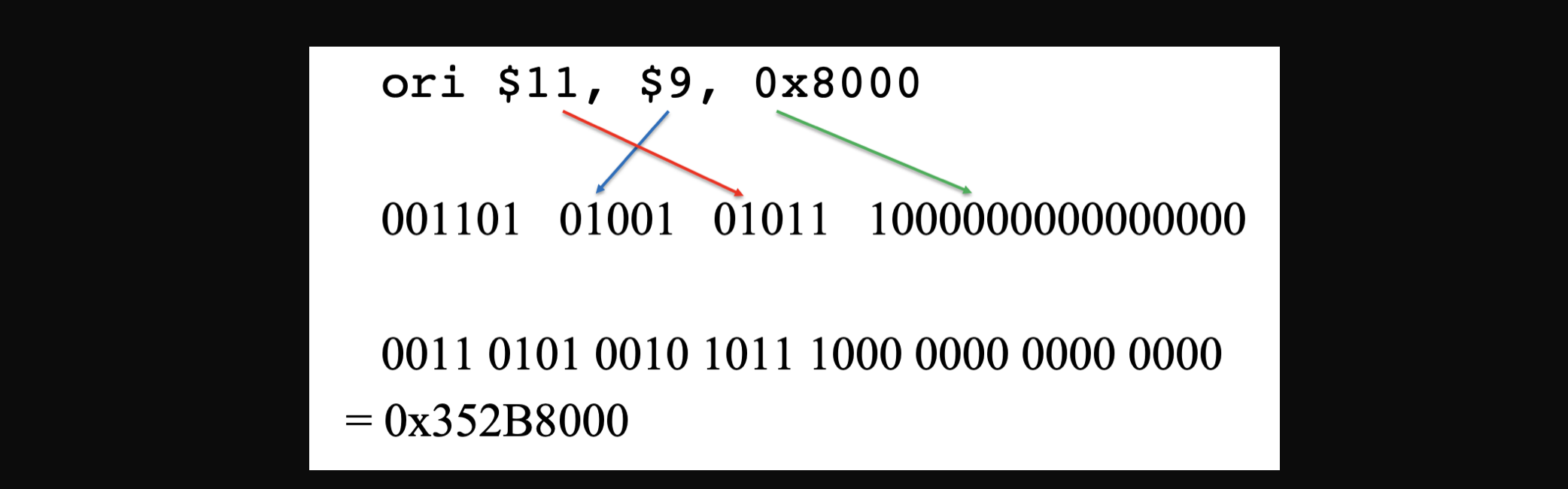
실제로 확인을 해봐도 저런 결과라는걸 아래의 사진을 통해 확인할 수 있습니다

---

Sign/Unsign Extension

지금까지의 내용을 공부하면서 이런 의문이 들었을 수 있습니다.

register값은 32bit인데 I-format에서의 constant는 16bit니까 대체 이 operands를 어떻게 연산하지...?

그래서 배워야할 내용이 extension에 관한 내용입니다. 결론부터 이야기하면 extension에는 Sign extension과 Unsign extension이 있고 해당 operand를 sign으로 볼지 unsign으로 볼지가 방식을 결정하게 됩니다. 무슨말인지는 설명을 쭉들으면 이해가될겁니다

우선 I-format의 logical Instruction을 먼저 생각해보면 우리가 ori나 andi연산을 할때 operande가 양수인지 음수인지 신경을 쓰지 않습니다. 그런 상황일때 16bit를 32bit로 extension해줄때는 unsign extension을 해주는데 방식은 아주아주 간단합니다 앞에 빈자리를 그냥 무조건 0으로 채워서 32bit를 만들면됩니다

그러면 addi의 연산을 한번 볼까요? 예를들어서 addi 연산의 constant에 -1이 들어가있다고 가정해봅시다. 16비트로 표현하면 1111 1111 1111 1111이 되겠네요. 근데 이걸 extension할때 unsign extension을 하면 앞에 0으로 16bit가 더 채워지고 0000 0000 0000 0000 1111 1111 1111 1111가 됩니다. 양수죠.. 우리는 음수를 가지고 연산을 하고싶은데 extension했더니 음수가 나와버립니다. 이런거처럼 우리가 constant의 sign을 고려해야하는 경우엔 sign extension해주면되는데 방법은 원래 16bit의 sign bit로 나머지 16bit를 채워주면됩니다. -1의 경우엔 sign bit가 1이니까 1111 1111 1111 1111 1111 1111 1111 1111이 되고 이걸가지고 register에 있는 32bit값을 가지고 연산을 진행하면됩니다.

spim에서 16진수 out of range에 관하여

이 내용은 cs라기보다는 spim에서의 내용이라 간단하게만 보고 넘어가면 좋습니다.

addi $10, $0, 0x8000

위와같은 assemble text를 실행하면 out of range라는 오류가 뜨는데 왜 그런 오류가 발생하는지 알아봅시다 기본적으로 spim은 sign로 숫자를 해석하는데 text에 16진수를 넣게되면 이 16진수를 unsign로 해석하게 됩니다. 즉, 16비트를 signed로 해석하는 spim 입장에선 최댓값이 32767인데 1000 0000 0000 0000이라는 수가 unsigned로 해석되어 32768로 되어서 spim입장에서는최대값을 넘어버린 값이 되어버린겁니다.

이러고나서 오류가 발생하는데 오류발생했을때 만약에 ok를 누르면 spim이 이 constant를 unsigned로 보고싶다고 판단해서 해당 constant를 unsign extension해서(부호가 무조건 양수니까 == 부호를 판단할 필요가 없으니까) 값을 넣어주는데 실제로 이런 오류가 발생한 이후에는

addi가 ori로 바뀌어서 실행되는걸 알수있고 이렇게 되면 해당 constant가 unsign extension되어서 값에 들어가게된다.

---

How to store a 32bit Constant to a register

우리가 I-format를 통해서 최대로 넣을 수 있는 bit는 16비트이지만 그냥 32비트를 넣고싶은데?라는 생각이 들수 있습니다

addi $s0, $0, 0x007d0900

이라는 연산을 하고 싶다고 생각해보죠 단순합니다 $s0 register에 addi연산을 통해 0x007d0900이라는 값을 넣어주고 싶은건데 근데 이것도 out of range가 뜨는데 이건뭐 sign unsign문제가 아니라 그냥 16bit안에 32bit값을 넣었으니 문제가 생기는거겠죠

이런 문제를 해결하기 위해 하나의 operator가 등장하는데 lui연산자입니다 load upper immediate instruction인데 그냥 쉽게말해서 앞에 16비트랑 뒤의 16비트를 쪼개서 저장하겠다는 아이디어라고 생각하면 편합니다

방금전예시에서 우리가 저장하고 싶은 constant는 0x007d0900이고 lui를 통해서 앞에 16비트+0으로된 16비트해서 총 32비트 operand를 저장합니다

lui $s0, 0x007d

그리고 나서 다음 연산으로 뒤의 16비트를 ori연산해줍니다

ori $s0, $s0, 0x0900

우선 천천히 따라가보면 $s0에는 0x007d0000라는 constant가 들어가있고 그 값과 0x0900이라는 값을 or연산해서 다시 $s0에 넣어주면되지만 ori연산을 할때 constant를 unsign extension해주기때문에 앞에 0으로 32bit를 채워서 or연산해주면 결과적으로 $s0에는 0x007d0900를 넣어줄 수 있게되는겁니다.

실제로 돌아가는 방식은 이러하고 우리가 처음봤던 text로 다시 돌아가보면

addi $s0, $0, 0x007d0900

이렇게 쓰면 out of range가 발생하는데 그냥 okay를 누르면 해당 연산을

lui $s0, 0x007d
ori $s0, $s0, 0x0900

이라는 연산으로 바꿔서 실행해주게되는데 이런걸 유사명령어라고 합니다