https://www.acmicpc.net/problem/11729
문제

입력
첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 20)이 주어진다.
접근과정
쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다. 이 조건 때문에 큰 어려움이 왔다.
세 번째 장대로 원판을 반복해서 옮길 때, 밑에 쌓여있는 원판보다 작은 원판들의 반경을 유동적으로 확인해서 1, 2, 3 장대 중 하나로 옮기는 과정이 필요하다.
그런데 과연 코드적으로 원판들의 반경을 판단하고 이리저리 옮기는 게 가능할까?
나는 아무래도 재귀 카테고리의 문제이며, 여기에 상향식 반복문으로 무언가를 해결하기는 어렵다고 생각했다.
그래서 맨 처음 접근했던 방법은 스택 3개를 준비했다. 왜냐하면 가장 위에서 원판을 빼며, 쌓기 때문에 스택이 적합하다고 생각했다. 먼저 내가 작성 했던 코드를 남긴다.
public class Main {
static int N;
static int count = Integer.MAX_VALUE;
static StringBuilder sb = new StringBuilder();
static Set<String> set = new HashSet<>();
public static void hanoi( Stack A, Stack B, Stack C, int count, StringBuilder sb ){
if( C.isFull() ) {
if( Main.count > count ) {
Main.count = count;
Main.sb = new StringBuilder(sb);
}
return;
} else if ( !set.add( Arrays.toString(A.stack) + Arrays.toString(B.stack) + Arrays.toString(C.stack)) )
return;
if( !A.isEmpty() ){
Stack tempA = new Stack(A);
int temp = tempA.pop();
if( (B.isEmpty() || B.pick() > temp)) {
StringBuilder tempSB = new StringBuilder(sb);
hanoi(tempA, new Stack(B, temp), new Stack(C), count+1, tempSB.append("1 2").append("\n"));
}
if( C.isEmpty() || C.pick() > temp ) {
StringBuilder tempSB = new StringBuilder(sb);
hanoi(tempA, new Stack(B), new Stack(C, temp), count+1, tempSB.append("1 3").append("\n"));
}
}
if( !B.isEmpty() ){
Stack tempB = new Stack(B);
int temp = tempB.pop();
if( A.isEmpty() || A.pick() > temp ) {
StringBuilder tempSB = new StringBuilder(sb);
hanoi(new Stack(A, temp), tempB, new Stack(C), count+1, tempSB.append("2 1").append("\n"));
}
if( C.isEmpty() || C.pick() > temp) {
StringBuilder tempSB = new StringBuilder(sb);
hanoi(new Stack(A), tempB, new Stack(C, temp), count+1, tempSB.append("2 3").append("\n"));
}
}
if( !C.isEmpty() ){
Stack tempC = new Stack(C);
int temp = tempC.pop();
if( A.isEmpty() || A.pick() > temp ) {
StringBuilder tempSB = new StringBuilder(sb);
hanoi(new Stack(A,temp), new Stack(B), tempC, count+1, tempSB.append("3 2").append("\n"));
}
if( B.isEmpty() || B.pick() > temp ) {
StringBuilder tempSB = new StringBuilder(sb);
hanoi(new Stack(A), new Stack(B,temp), tempC, count+1, tempSB.append("3 1").append("\n"));
}
}
} // hanoi
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = Integer.parseInt(br.readLine());
N = n;
Stack stack = new Stack(N);
while(n-->0){
stack.add(n+1);
}
hanoi( stack, new Stack(N), new Stack(N), 0, new StringBuilder() );
System.out.println(count);
System.out.println(sb);
} // main
static class Stack{
int[] stack;
int index;
Stack(int capacity){
this.stack = new int[capacity];
this.index = -1;
}
Stack(Stack stack){
this.stack = Arrays.copyOf(stack.stack, stack.stack.length);
this.index = stack.index;
}
Stack(Stack stack, int num){
this.stack = Arrays.copyOf(stack.stack, stack.stack.length);
this.index = stack.index;
this.stack[++index] = num;
}
public void add(int num){
stack[++index] = num;
}
public int pop(){
int pop = stack[index];
stack[index--] = 0;
return pop;
}
public int pick(){
return stack[index];
}
public boolean isFull(){
return index == stack.length-1;
}
public boolean isEmpty(){
return index == -1;
}
}
}매 함수 호출마다 3개의 스택이 비어있는지 확인하고 비어있지 않다면 다른 스택에 가장 위에 있는 원판을 넣는다.
만약 이때, 2번 장대에서 1번 장대로 원판을 넣을 때 1번 장대의 가장 위에 있는 원판이 2번 장대에서 들어오는 원판보다 크다면 원판을 넣지 않고 함수 또한 호출하지 않는다.
이렇게 했을 때 문제점이 있는데, 반드시 스택오버플로우 에러가 발생한다는 점이다. 왜냐하면 모든 스택(장대)에서 다른 장대로 원소를 옮길 수 있기만 하면 함수를 호출하는 방식이기 때문이다.
즉, 1번 장대에서 2번 장대로 원판 1을 옮겼는데, 다음 함수에서 다시 반대로 2번 장대에서 1번 장대로 원판 1을 다시 옮길 수도 있다는 뜻이 된다. 그래서 스택오버플로우 에러가 발생한다.
이를 막을 방법을 찾아야했는데, 내가 사용한 방법은 매 함수마다 HashSet에 세 개의 스택 상태를 저장하고 확인하는 것이다.
만약 초반 함수에서 세 개의 스택 상태들을 저장한 상태라고 가정하자. 다음에 재귀에 의해서 원판이 이리저리 움직이다가 초반에 발생했던 스택 상태와 동일하다면, 해시맵을 통해 이를 파악하고 해당 함수를 조기 종료시킨다.
이 과정을 거쳐 나는 1번 장대에서 3번 장대로 모든 원판을 옮기는 데에는 성공했다. 하지만 최소의 움직임으로 원판을 옮기는 데에는 실패했다.
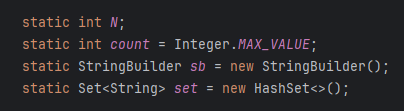

매개변수에 count를 선언해 다음 함수에 count+1을 넘겨주는 식으로 작성한 뒤, 3번 스택(장대)가 원판의 개수 N만큼 가득 찼다면 전역 변수에 선언되어있는 count에 총 움직임 횟수를 뜻하는 count를 저장하는 방법을 사용했다.
하지만, 나는 결국 나의 접근법이 아예 틀렸다는 것을 깨달았다.. 1번 장대에서 3번 장대로 모든 원판을 옮기는 데에는 성공하지만, 여전히 최소 움직임으로 옮기는 것이 되지 않는다. 나는 print 함수를 통해 스택의 상태를 매 재귀 함수마다 확인해보았다.
아아.. 나는 스택오버플로우를 막기 위해 모든 스택의 상태가 동일하다면 해당 함수를 조기 종료시키도록 만들었었다. 그리고 내가 만든 코드로인해 원판들은 1, 2, 3 장대에서 이리저리 움직인다. 내가 원했던 점은 아래 이미지와 같았지만..
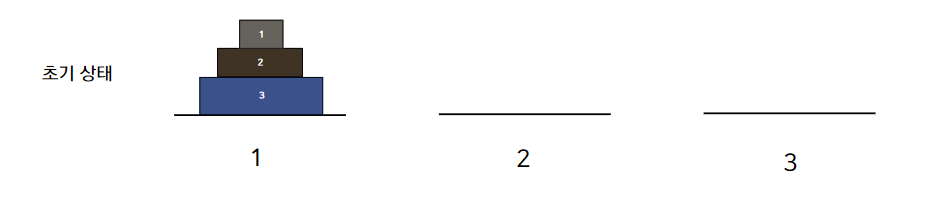
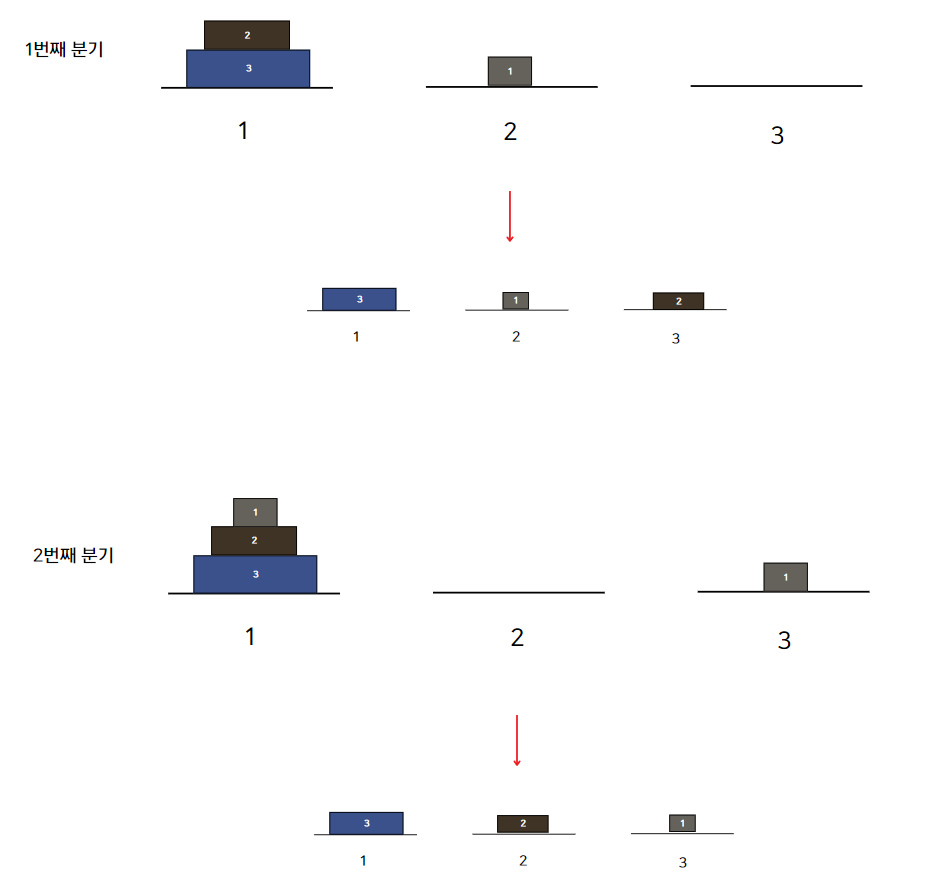
결과는..
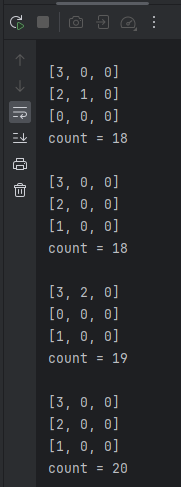
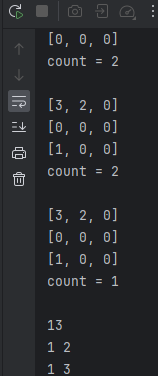
1번 장대:[3, 2, 1] 2번 장대: [0, 0, 0] 3번 장대: [1, 0, 0] 은 count가 19일 때 한 번 일어났던 상태라 count가 1인 상태가 조기 종료되는 것이었다.
즉, 분기를 내가 통제할 수 없다.. 일단 한번 깊게 들어갔다가 빠져나오는 구조였던 것이다.
문제를 푸는데 너무 많은 시간 소요하기도 했고 코드의 효율이나 메모리 소비가 엄청나 이미 안좋은 코드인 것 같아, 구글링을 통해 풀이를 찾아보았다.
나는 몰랐었는데, 하노이의 탑은 매우 유명한 재귀 문제 예제였고, 덕분에 좋은 풀이방법을 찾았다.
하노이의 탑의 가장 중요한 포인트는 원판의 개수가 n개일 때 가장 밑에 있는 원판을 3번 장대로 옮기는 것이다. 그리고 그러기 위해선 가장 밑에 있는 원판을 제외한 나머지 원판을 가운데 장대인 2번 장대로 옮겨야한다. 그리고 맨 밑 원판을 3번 원판으로 옮긴 후 2번 장대에 있던 n-1개의 원판(가장 밑 원판을 제외한)들을 3번 원판으로 옮긴다.
이 패턴이 반복되므로 이를 토대로 재귀 코드를 작성한다.
public class Main {
static StringBuilder sb = new StringBuilder();
static int count = 0;
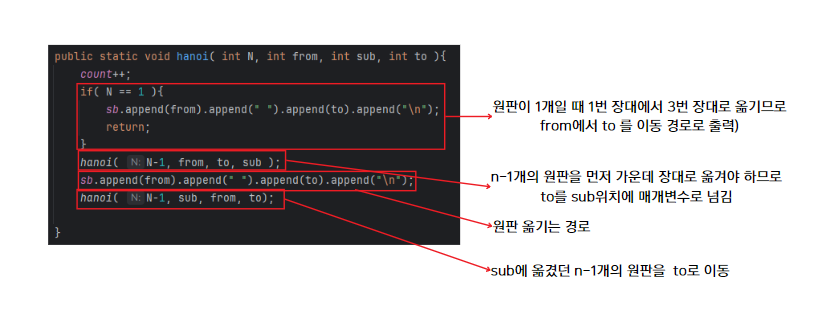
public static void hanoi( int N, int from, int sub, int to ){
count++;
if( N == 1 ){
sb.append(from).append(" ").append(to).append("\n");
return;
}
hanoi( N-1, from, to, sub );
sb.append(from).append(" ").append(to).append("\n");
hanoi( N-1, sub, from, to);
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
hanoi( N, 1, 2, 3 );
System.out.println(count + "\n" + sb.toString());
}
}
나가는 글
사실 여러 풀이 코드와 설명을 들어도 해당 코드가 어떻게 문제를 해결하는지, 어떻게 그게 가능한지 직관적으로 이해가 잘 되지는 않았다.
내 머리가 나쁜건가 자책하다가도, 공부를 시작하는 많은 사람들이 재귀 기법과 하노이의 탑에서 많이들 막힌다고 하니 그것에 위안 삼으며 다른 재귀 문제를 접해보며 익숙해져야겠다고 생각했다.

