https://www.acmicpc.net/problem/2580
문제

이미지 출처: 백준
입력
아홉 줄에 걸쳐 한 줄에 9개씩 게임 시작 전 스도쿠판 각 줄에 쓰여 있는 숫자가 한 칸씩 띄워서 차례로 주어진다. 스도쿠 판의 빈 칸의 경우에는 0이 주어진다. 스도쿠 판을 규칙대로 채울 수 없는 경우의 입력은 주어지지 않는다.
풀이과정
스도쿠에서 빈 칸을 채우는 방식은 가로줄과 세로줄에 1부터 9까지의 숫자가 한 번씩만 나타나야 하며, 굵은 선으로 구분되어 있는 3x3 정사각형 안에도 1부터 9까지의 숫자가 한 번씩만 나타나야한다고 한다.
풀이를 위해 아래의 예시가 주어진다고 가정해보자. 0은 빈칸이라고 가정한다.
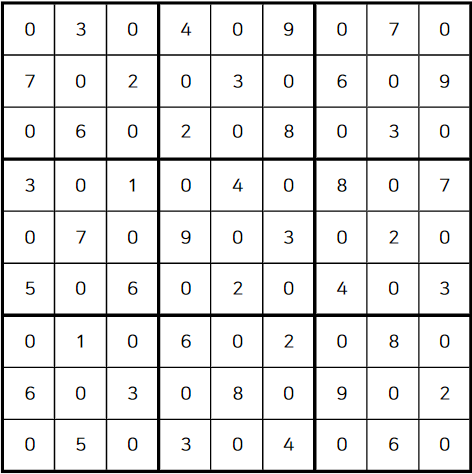
첫 번째 줄을 보면 채워지지 않은 칸이 무척 많다. 이런 경우 칸을 채울 수 있는 수들 중 하나씩 대입해보며 스도쿠를 풀어나가는 수 밖에 없다.
첫 번째 칸부터 살펴보자. 해당 칸에 채워질 수 있는 수는 규칙에 의해 다음과 같다.
가로줄 1, 2, 5, 6, 8
세로줄 1, 2, 4, 8, 9
3x3 정사각형 1, 4, 5, 8, 9
위 숫자들이 모두 해당 칸에 채워질 수 있는 것은 아니다. 만약 해당 칸에 3x3 정사각형 규칙에 의한 숫자 4가 들어간다면 가로줄에 위치한 4와 곂치게된다. 따라서 세 개의 규칙으로 얻은 숫자의 합집합이 아닌 교집합이 빈 칸에 채워질 수 있는 숫자이다.
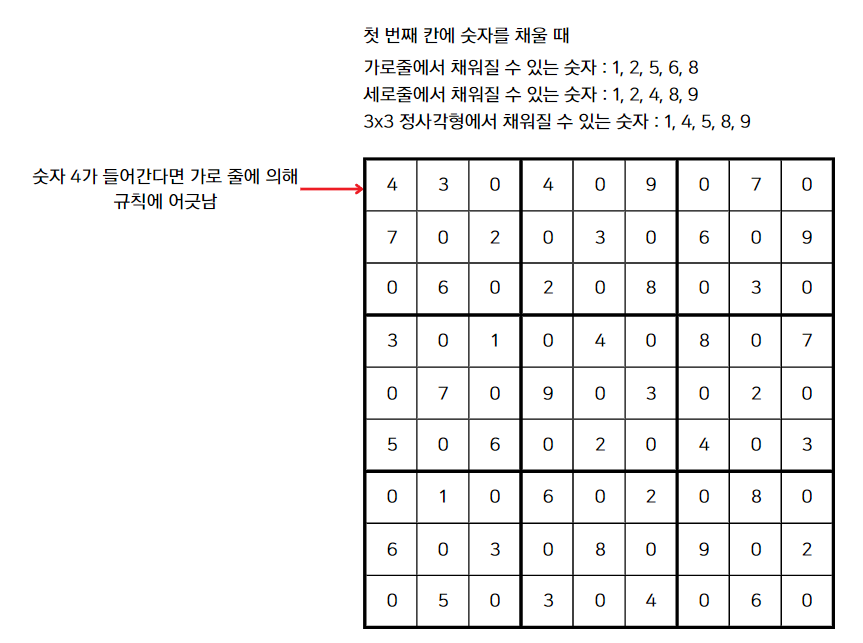
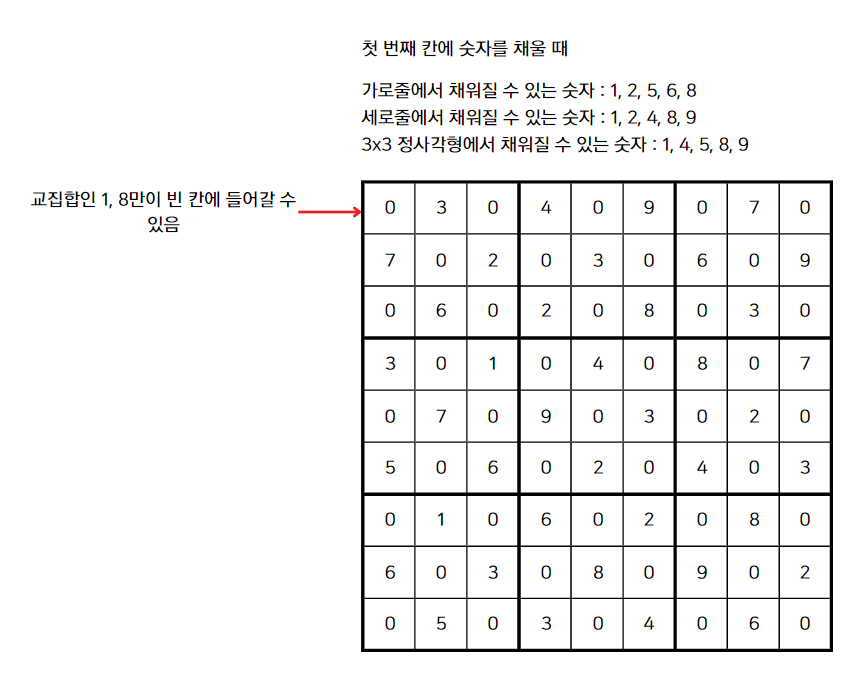
따라서, 첫 번째 칸에는 1 또는 8이 들어갈 수 있다는 것을 알았다. 빈 칸에 1을 집어넣고 다음 단계까지만 함께 살펴보자.
세 번째 빈 칸을 채울 때의 경우이다.
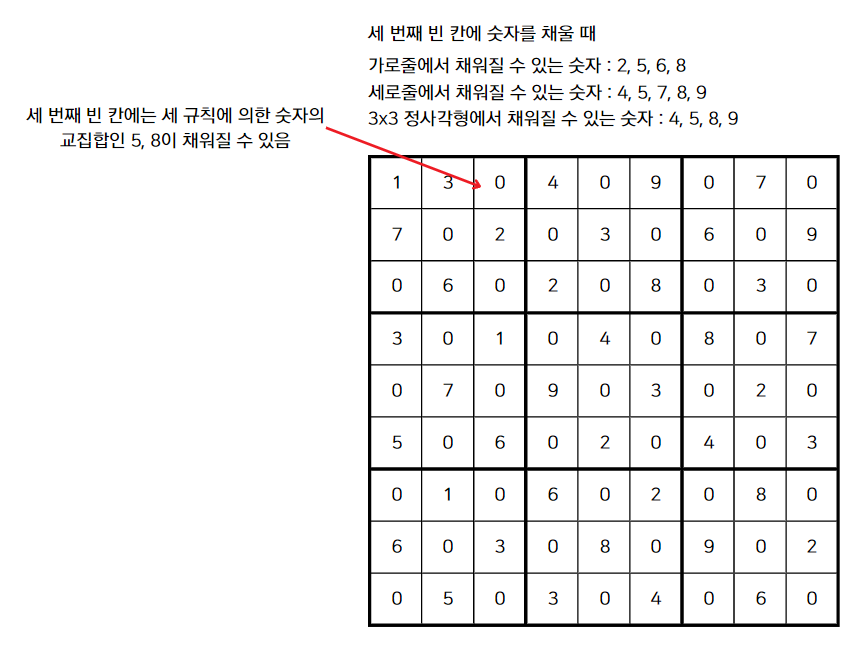
이런 식으로 빈 칸에 넣을 수 있는 경우의 수를 모두 넣어가며 스도쿠를 완성할 수 있다. 이때 백트래킹이 매우 유용한 기법으로 사용될 수 있다.
다음은 java로 구현한 풀이 코드이다.
public class Main {
// 9x9 스도쿠
static int[][] arr = new int[9][9];
// 빈 칸이 들어있는 좌표 리스트
static List<String> zeroArr = new ArrayList<>();
// 스도쿠가 완성됐는지 확인하는 플래그
static boolean isOver = false;
// 가로, 세로, 3*3 범위의 교집합 리스트 반환 메서드
public static List<Integer> find( int row, int col ){
int[] tempArr = new int[10];
// 가로 줄
for( int tCol = 0; tCol < 9; tCol++ ) {
tempArr[arr[row][tCol]]++;
}
// 세로 줄
for( int tRow = 0; tRow < 9; tRow++ )
tempArr[arr[tRow][col]]++;
// 3x3 정사각형
int startRow = row/3*3, startCol = col/3*3;
for( int tRow = startRow; tRow <= startRow+2; tRow++ ){
for( int tCol = startCol; tCol <= startCol+2; tCol++ ){
tempArr[arr[tRow][tCol]]++;
}
}
// 만약 세 규칙으로 스도쿠 판을 살펴도 0인 숫자가 있다면
// 해당 숫자는 교집합에 포함
List<Integer> zero = new ArrayList<>();
boolean flag = false;
for( int i = 1; i <= 9; i++ ){
if(tempArr[i] == 0) {
zero.add(i);
flag = true;
}
}
// 만약 교집합에 숫자가 하나도 포함되어있지 않는다면
// 해당 스도쿠 조합은 규칙에 어긋남
return !flag ? null : zero;
}
// 풀이 메서드
public static void solve( int index ){
// true라면 스도쿠가 완성되었다는 뜻이므로
// 조기 종료
if( isOver )
return;
// 빈 칸의 좌표를 담은 리스트의 크기와
// index가 같거나 크면 isOver 변수를 true로 만들고
// 스도쿠 판 출력
if( index >= zeroArr.size() ) {
print();
isOver = true;
return;
}
// 빈 칸 좌표
int row = zeroArr.get(index).charAt(0)-48, col = zeroArr.get(index).charAt(2)-48;
List<Integer> zero = find( row, col );
// 리스트가 null이라면 해당 스도쿠 조합은
// 규칙에 어긋남. 조기 종료
if( zero == null ) {
return;
}
// 교집합 숫자 개수만큼 반복
for( int i = 0; i < zero.size(); i++ ){
// 빈 칸 위치에 교집합 숫자 대입
arr[row][col] = zero.get(i);
// 다음 빈 칸 위치로 이동
solve( index+1 );
// 다시 0 대입
arr[row][col] = 0;
}
}
// 스도쿠 판 출력 메서드
public static void print(){
StringBuilder sb = new StringBuilder();
for (int row = 0; row < 9; row++){
for(int col = 0; col < 9; col++){
sb.append(arr[row][col]);
if(col != 8) sb.append(" ");
}
sb.append("\n");
}
System.out.println(sb);
}
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
for (int row = 0; row < 9; row++) {
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
for (int col = 0; col < 9; col++) {
int num = Integer.parseInt(st.nextToken());
arr[row][col] = num;
// 입력 값이 0이면 zeroArr에 좌표 저장
if( num == 0 )
zeroArr.add( row + " " + col );
}
}
solve( 0 );
} // main e
} // class e나가는 글
본 풀이는 다른 정답자들의 코드에 비해 메모리 효율이나 속도 효율 측면에서나 모두 비효율적인 코드이다. 물론 아직 초심자 입장에선 풀었다는 것만으로도 자축할만한 일이지만 더 성장하기 위해선 어떤 점을 보완해야할지 생각해보는 것도 중요한 것 같다.

