Tree란?
계층 구조(hierarchical structure)를 나타내는 자료구조입니다. Level이 존재하는 Graph라 생각해도 무방합니다. 트리는 노드(graph의 vertex == node와 동일)와 간선(graph의 edge와 동일)으로 구성되며, 간선은 노드들을 연결합니다. 루트라고 불리는 하나의 특별한 노드(시작 노드)에서 다른 노드들을 연결하고, 각 노드는 자신의 부모 노드와 자식 노드를 가지게 됩니다.
Tree의 종류
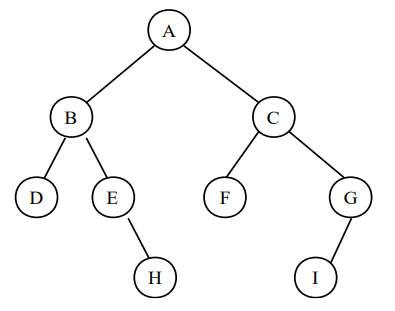
1. 이진트리(Binary Tree)
이진트리는 하나의 노드가 최대 두 개의 자식 노드를 가지는 자료구조입니다. 이진트리는 매우 간단한고 기본적인 형태로서, 많은 다른 트리 자로구조들이 이진트리를 기반으로 만들어졌습니다. 이진트리의 각 노드는 왼쪽 자식 노드와 오른쪽 자식 노드를 가질 수 있습니다.
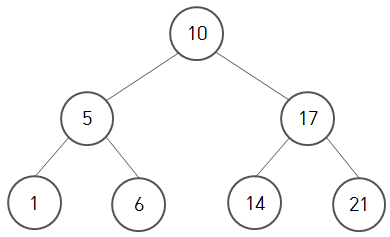
2. 이진탐색트리(Binary Search Tree)
이진탐색트리는 이진트리의 일종으로, 모든 노드에 대해서 왼쪽 자식 노드는 현재 노드보다 작은 값을, 오른쪽 자식 노드는 현재 노드보다 큰 값을 가지도록 구성됩니다. 이진탐색트리는 정렬된 데이터를 저장하고 검색하는 데 매우 효율적입니다.
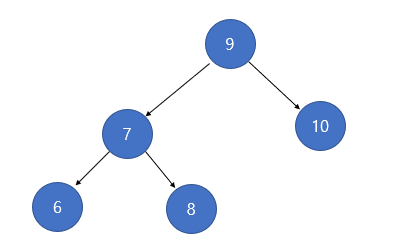
3. AVL 트리(Adelson-Velsky and Landis Tree)
AVL트리는 컴퓨터 과학에서 이 트리의 발명자의 이름을 가져온 자가 균형 이진 탐색 트리입니다.
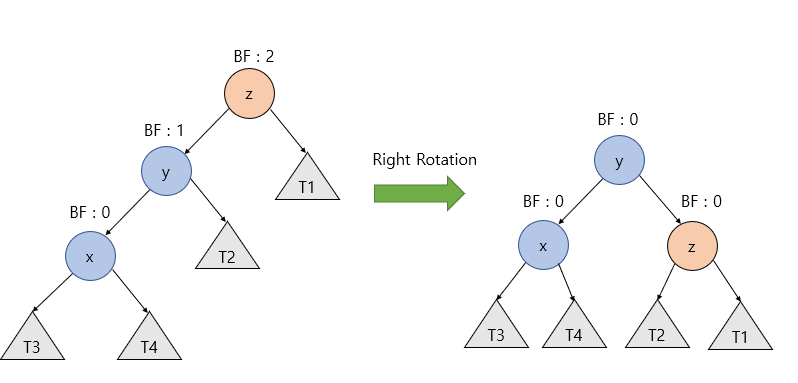
AVL 트리는 균형잡힌 이진탐색트리로서, 각 노드의 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 1 이하인 트리입니다. 높이 차이가 1보다 크게 나게 되면 회전(Rotaion)이라는 균형을 다시 잡는 과정을 작업을 수행합니다. 삽입, 삭제, 검색 등의 연산에서 높은 성능을 보장합니다.
회전의 예시
4. 레드 - 블랙 트리(Red-Black Tree)
레드-블랙 트리는 균형잡힌 이진탐색트리로서, 일종의 자기 균형 이진 탐색 트리(Self-Balancing Balanced Search Tree)입니다. 각 노드에 레드(Red) 또는 블랙(Black) 색상을 지정하여 균형을 유지합니다. 삽입, 삭제, 검색 등의 연산에서 높은 성능을 보장하면서도 AVL 트리보다는 구현이 쉽습니다. 또한 균형을 잡는 과정에서 AVL은 O(logN)이지만 RB Tree는 O(1)입니다.
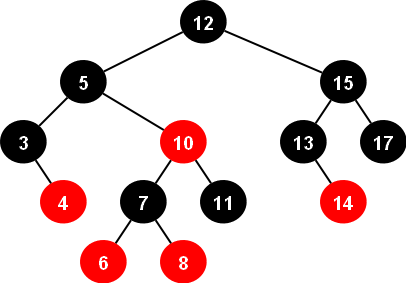
RB 트리의 특징
- 각 노드는 레드 or 블랙입니다.
- 루트 노드와 모든 NIL(Not In List 혹은 Null) 노드들은 항상 색이 검은색으로 설정됩니다.
NIL 노드는 일종의 가상 노드로, 실제 노드가 아니며 NULL 포인터를 가리키는 노드입니다. 따라서, NIL 노드는 실제 메모리 상에서 존재하지 않는 가상의 노드입니다. 이러한 NIL 노드는 Red-Black Tree에서 특정 목적을 위해 사용됩니다. 예를 들어, NIL 노드를 사용하여 모든 리프 노드가 같은 높이에 위치하도록 보장할 수 있습니다.
또한, Red-Black Tree의 구현에서 NULL 포인터는 일반적으로 노드가 없음을 나타내므로, NIL 노드가 NULL 포인터를 가리키도록 함으로써, 트리의 구현이 단순화됩니다. 즉, NIL 노드를 NULL 포인터로 설정하면 더 많은 메모리를 절약할 수 있으며, 코드 구현도 단순화됩니다.
- 레드 노드의 자식으로 레드가 있으면 안됩니다. 레드의 자식은 모두 블랙입니다.
- 블랙 노드의 자식은 레드, 블랙 둘 다 가능합니다.
- 루트 노드에서 모든 리프 노드까지의 경로에 대해서 거치는 블랙 노드의 숫자는 같습니다.
5. B-Tree
B-Tree는 대용량의 데이터를 저장하고 검색하기 위해 고안된 트리 자료구조 중 하나입니다. B-트리는 자식 노드의 수가 2개 이상인 일반적인 트리와 달리 각 노드당 자식 노드의 수가 여러 개인 다중 자식(multiway) 트리입니다.
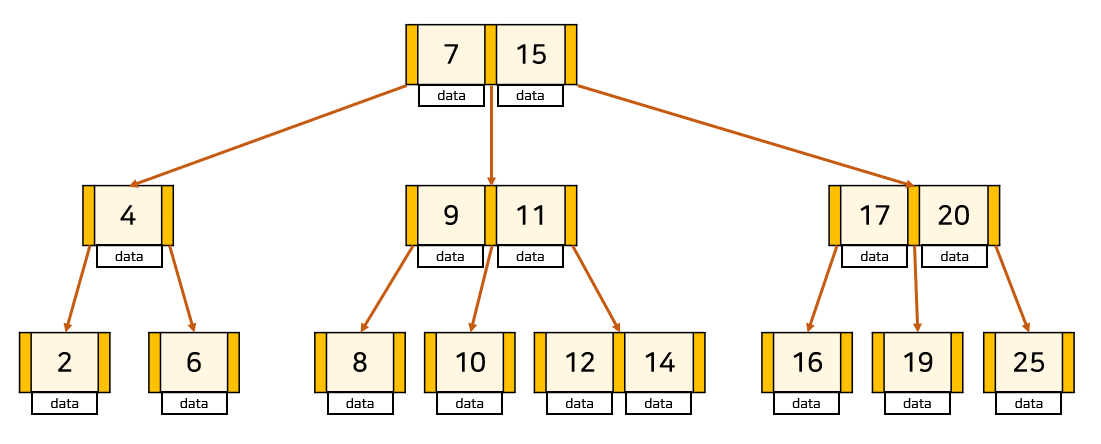
B - 트리의 특징
- 모든 리프 노드(leaf node)는 같은 레벨(level)에 있습니다.
- 내부 노드(internal node)는 여러 개의 자식 노드(child node)를 가질 수 있습니다.
- 각 노드는 하나 이상의 키(key)와 그에 대응하는 값(value) 또는 자식 노드의 포인터를 가지고 있습니다.
- 노드의 키(key)는 정렬되어 있으며, 모든 리프 노드(leaf node)의 키(key)는 서로 다릅니다.
6. B+ Tree(B plus Tree)
B+ 트리는 B-트리의 변형으로 B-트리와 동일하게 DB에서 사용되는 자료구조입니다.
B+트리는 B-트리와 달리 리프 노드(Leaf Node)에만 실제 데이터를 저장하며, 내부 노드(Internal Node)에는 키(Key)만 저장합니다. 또한 리프 노드들은 연결 리스트로 연결되어 있어서 범위 검색(range search)과 같은 작업에 매우 유용합니다.
B+트리는 내부 노드에 키만 저장하므로 리프 노드에 저장된 데이터 수가 더 많아질 수 있습니다. 또한 리프 노드는 연결 리스트로 구성되어 있기 때문에 범위 검색에 효율적입니다. 또한 B+트리는 대부분의 데이터베이스에서 인덱스(Index) 구현에 사용됩니다.
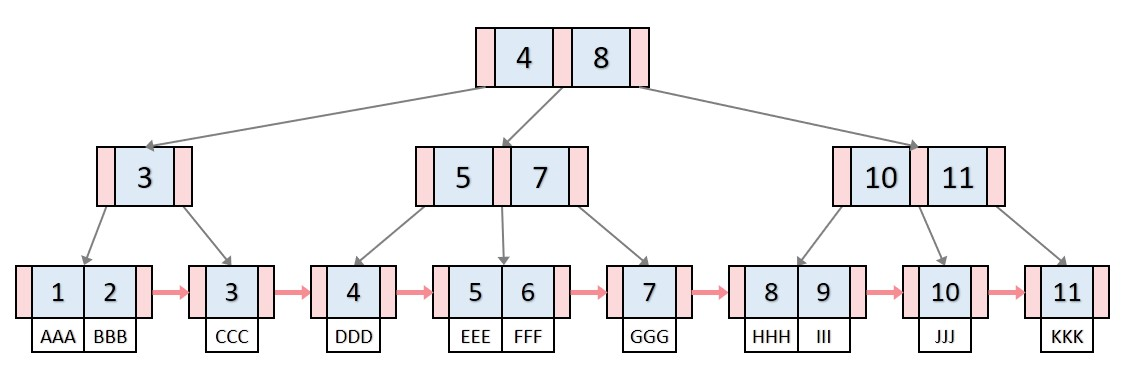
B+ 트리의 특징
- 모든 리프 노드는 같은 레벨(level)에 있습니다.
- 내부 노드는 키(key)만을 가지며, 리프 노드에 저장된 데이터와는 관련이 없습니다.
- 모든 리프 노드는 연결 리스트로 구성되어 있으며, 이를 통해 범위 검색(range search)이 용이합니다.
- 각 노드는 하나 이상의 키(key)와 그에 대응하는 값(value) 또는 리프 노드의 포인터를 가지고 있습니다.
트리의 활용
1. 파일 시스템(File System)
파일 시스템은 파일과 디렉토리를 저장하고 관리하는 운영 체제의 일부입니다. 대표적인 파일 시스템인 NTFS, ext4, HFS+ 등은 모두 트리 자료구조를 사용하여 파일과 디렉토리를 저장하고 관리합니다. 파일 시스템의 루트 디렉토리가 트리의 루트 노드이고, 각 디렉토리가 트리의 노드이며, 파일이나 하위 디렉토리가 트리의 자식 노드가 됩니다.
2. 데이터베이스 인덱스(Database Index)
데이터베이스에서 인덱스는 데이터베이스 테이블에서 레코드를 빠르게 검색하기 위해 사용됩니다. 대부분의 데이터베이스 인덱스는 B-트리나 B+트리를 사용하여 구현됩니다. 인덱스의 키 값은 트리의 노드에 저장되고, 각 노드의 자식 노드는 키 값보다 크거나 작은 값을 가지고 있는 레코드를 가리킵니다. 이렇게 인덱스를 구현하면 테이블에서 특정 레코드를 검색하는 데 걸리는 시간을 대폭 줄일 수 있습니다.
3. 네트워크 라우팅(Network Routing)
인터넷에서 네트워크 라우팅은 패킷이 목적지로 전달되기 위해 어떤 경로를 통해 전송되어야 하는지 결정하는 것입니다. 네트워크 라우팅에서도 트리 자료구조가 사용됩니다. 라우터는 각 인터페이스에 대한 정보를 저장하는 노드이며, 각 라우터 간 연결은 트리의 간선(edge)로 표현됩니다. 이렇게 트리를 사용하여 네트워크 라우팅을 수행하면 더욱 효율적인 패킷 전달이 가능해집니다.
4. GUI 위젯(GUI Widget)
GUI 위젯은 그래픽 사용자 인터페이스(Graphical User Interface)를 구현하는 데 사용되는 구성 요소입니다. 대부분의 GUI 라이브러리(GUI Library)는 트리 자료구조를 사용하여 위젯들을 구성합니다. 예를 들어, 트리뷰(Tree View) 위젯은 각 노드가 하위 노드들과 연결된 트리 형태로 표현됩니다. 트리뷰는 대개 파일 시스템 탐색기와 같이 계층적인 데이터를 표시하는 데 많이 사용됩니다. 또한, 트리를 이용하여 트리 메뉴(Tree Menu)나 트리 컴보박스(Tree Combo Box) 등의 위젯도 구현할 수 있습니다.
5. 컴파일러(Compiler)
컴파일러는 소스 코드를 목적 코드로 변환하는 프로그램입니다. 컴파일러의 구현에서도 트리 자료구조가 사용됩니다. 예를 들어, 컴파일러는 소스 코드를 파싱하여 추상 구문 트리(Abstract Syntax Tree, AST)를 생성하고, 이를 바탕으로 목적 코드를 생성합니다. 추상 구문 트리는 소스 코드의 구조를 나타내는 트리이며, 각 노드는 구문 구성 요소에 해당합니다.
6. 인공지능(AI)
인공지능 분야에서도 트리 자료구조가 많이 사용됩니다. 예를 들어, 결정 트리(Decision Tree)는 데이터 분류, 회귀 등의 문제를 해결하기 위해 사용됩니다. 또한, 알파벳벳트리(Alpha-Beta Tree)는 게임 플레이에서 최적의 수를 찾는 데 사용됩니다.