특성공학
특정 값들을 조합하여 새로운 특성을 가공
pandas
이번에는 값을 가져올때, pandas를 통해 값을 가져왔다
import pandas as pd df = pd.read_csv("https://bit.ly/perch_csv_data) perch_full = df.to_numpy() print(perch_full) ... from sklearn.model_selection import train_test_split train_input, test_input, train_target, test_target = \ train_test_split(perch_full, perch_weight, random_state=42)
변환기
다양한 특성을 얻기 위하여, 변환기를 통해 다양한 특성을 조합하였다
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(include_bias=False)
poly.fit([[2,3]])
print(poly.transform([[2,3]]))
# 출력값 : [[2,3,4,6,9]]위 코드를 통해 2,3과 2*2,2*3,3*3 의 값을 얻을 수 있었다
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)모델 훈련하기
이제 위에서 얻은 특성을 통하여 다시 선형회귀모델을 훈련시켜보자
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target)) # 0.996...
print(lr.score(test_poly, test_target)) # 0.971...꽤나 나쁘지 않는 점수를 출력함을 볼 수 있다
더 정확한 훈련을 위해 차수를 추가하면 어떻게 될까? 5차항 그래프를 훈련시켜보자
poly = PolynomialFeatures(include_bias=False, degree=5)
...
print(lr.score(train_poly, train_target)) # 0.999...
print(lr.score(test_poly, test_target)) # -144.404...규제
갑자기 테스트 세트에서 말도 안 되는 점수를 출력하였다. 왜 그럴까?
모델이 훈련 세트를 너무 과도하게 학습할시, 테스트 세트 가 부적합 하다고 판단, 실제 다른 샘플들에서도 부정확한 값들을 나타낼 수 있다
이를 위해 우리는 모델이 훈련 세트를 덜 학습하도록 규제가 필요하다
스케일
먼저 규제를 진행하기전에 전처리 작업을 해주자
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(train_poly)
train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)릿지 Ridge
from sklearn.linear_model import Ridge
ridge = Ridge()
ridge.fit(train_scaled, train_target)
print(ridge.score(train_scaled, train_target)) # 0.990
print(ridge.score(test_scaled, test_target)) # 0.979이때 우리는 alpha값을 통해 규제의 강도를 설정한다
alpha가 크면 과소적합이 될 수 있고,
alpha가 작으면 과대적합이 될 수 있다
적절한 alpha값은 그래프를 그려 확인 가능하다
from sklearn.linear_model import Ridge
import matplotlib.pyplot as plt
train_score = []
test_score = []
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
ridge = Ridge(alpha = alpha)
ridge.fit(train_scaled, train_target)
train_score.append(ridge.score(train_scaled, train_target))
test_score.append(ridge.score(test_scaled, test_target))
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha2')
plt.ylabel('R^2')
plt.show()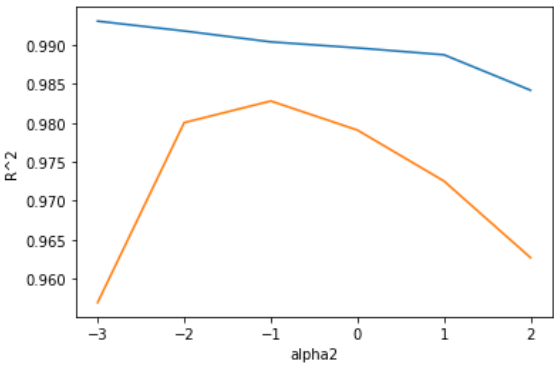
그래프를 통해 확인결과, -1일때 가장 유사한 점수를 보인다
위 그래프를 근거로 을 alpha값으로 지정하면 된다.
라쏘 Lasso
from sklearn.linear_model import Lasso
lasso = Lasso()
lasso.fit(train_scaled, train_target)
print(lasso.score(train_scaled, train_target)) # 0.989...
print(lasso.score(test_scaled, test_target)) # 0.980...라쏘또한 alpha를 통해 규제를 통제하여보자
import matplotlib.pyplot as plt
train_score = []
test_score = []
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]
for alpha in alpha_list:
lasso = Lasso(alpha=alpha, max_iter=10000)
lasso.fit(train_scaled, train_target)
train_score.append(lasso.score(train_scaled, train_target))
test_score.append(lasso.score(test_scaled, test_target))
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha2')
plt.ylabel('R^2')
plt.show()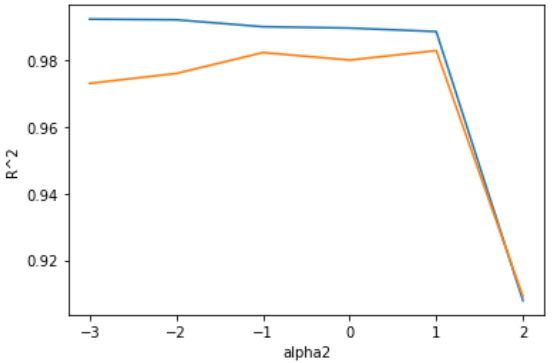
값이 비슷한 1을 통해
lasso = Lasso(alpha=10)
lasso.fit(train_scaled, train_target)
print(lasso.score(train_scaled, train_target)) # 0.98...
print(lasso.score(test_scaled, test_target)) # 0.98...릿지 vs 라쏘
릿지
알고리즘이 가능한 모든 샘플을 포함하려 함
변수가 많으면 과대적합의 위험 증가
다중공선성 존재시 변수간 상관관계에 따라 계수로 다중공선성이 분산되어 유리
라쏘
최소한의 변수만을 포함하려고 함
변수 선택이 가능, 계수가 커질 수 있다
다중공선성 존재시 특정 변수만을 사용하기에 불리함


