배열(array) - 한 자료형의 여러 값들이 메모리 상에 모여있는 구조
컴퓨터는 해당 값들에 접근할 때 array의 index 하나하나 접근하며, 대표적인 예로, 아래 두가지 탐색 방법이 있음.
빠른 순서 : O(1), O(log n), O(n), O(n log n), O(n^2)
탐색법
-
선형탐색 : array의 index를 처음부터 끝까지 하나씩 증가시키면서 방문하여, 그 값이 속하는지(있는지)를 검사함 > O(n), Ω(1)
-
이진탐색 : array가 정렬되어 있을 때, 배열 중간의 index부터 시작하여 찾고자 하는 값과 비교하며 그보다 작거나 큰 index로 이동을 반복하며 검사함 (정렬에 시간이 오래걸린다는 점을 고려해야 함) > O(log n), Ω(1)
Algorithm 관련 표기법
-
Big O : On the order of (~만큼의 정도로 커지는) 실행 시간의 상한을 나타냄. (최악의 상황 고려)
-> 조금 더 검색해본 결과, 이걸 이용해서 시간복잡도, 공간복잡도를 나타내는 듯 하다..! -
Big Ω : 실행 시간의 하한을 나타냄. (최상의 상태. 가장 알고리즘이 잘 되었을 경우)
-
대문자 theta : 어떤 알고리즘의 상한선과 하한선이 같을 때 Theta 표기법 사용. (예: selection sort, merge sort)
정렬법
-
bubble sort : 두 개의 인접한 data의 value를 비교하면서, 위치를 swap하는 방식으로 정렬하는 방법 (좁은 범위 정렬) > O(n^2), Ω(n^2)
-> 만약, 전부 정렬이 되었음을 확인하고(swap이 발생하지 않을 때) 그 때 알고리즘을 멈춰주는 기능을 넣는다면, 최선의 경우는 Ω(n)이 될것이다. -
selection sort : 배열 안의 자료 중, 가장 작은 수 (or 가장 큰 수)를 찾아 첫번째 (or 마지막)위치의 수와 교환해주는 정렬 방식 (교환 횟수는 최소화 하지만, 자료 비교 횟수는 증가함) > O(n^2), Ω(n^2)
-
merge sort : 왼쪽을 정렬하고, 오른쪽을 정렬한 뒤 Merge. 정렬을 할 요소가 없으면 return을 한다는게 기본 원리. array의 원소가 한 개가 될 때까지 계속해서 반으로 나눈 후에 다시 합쳐나가면서 정렬을 함. > O(n log n), Ω(n log n)
재귀함수
-
recursion :
-> 찾아본 결과, 듣기는 많이 듣고, LIFO니 FIFO니 했던 stack, heap과 같은 자료구조와 관련이 있었고, 알고보니 재귀는 "Stack"이라는 자료구조였다.
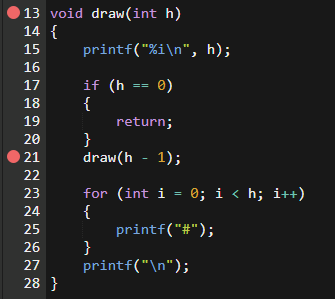
해당 사진은, 재귀함수 관련 수업 때 받아적은 코드이다. 와 이거 하면서 너무 어이가 없었다. 디버깅을 해보니까, draw()라는 함수가, 내가 입력한 h값이 10이라면, draw(10), draw(9), draw(8), ... , draw(1), draw(0) 이렇게 실행이 먼저 되는데, 또 for문으로는 죽어도 안넘어간다 ㅋㅋㅋㅋㅋ (미침)
for문 부터는 draw(1), draw(2), draw(3), .... , draw(10) 이렇게 실행되는 것이다.. 진짜 돌아버리는줄 알았다^^ 이게뭘까 싶어서^^.. 그래서 이건 디버깅만으로는 할 수 없는 어떤 "특별한 개념"이 있다 판단하여.. 여러 곳을 돌아다니며 공부를 해봤다. 내가 가장 알기쉽게 설명해주신 분은 이분이었다. 감사합니다 ㅠㅠ..
이분의 그림 구조를 보고, 어? 이거 노마드 코더, 생활 코딩에서 봤던 stack이구나 싶었다. (코딩도 아직 잘 모르면서 자료구조 영상은 또 봐놨다.. 중요하대서..) 너무 어렵고 어이가 없었지만, 그래도 계속 귀에 박혀만 있던 stack 자료구조의 LIFO를 첫 경험한 것이었기에, 기분이 묘했다. 드디어 그 중요하다는 자료구조 "stack"의 실제 예제를 보았구나.. 이런 경험을 할 수 있게 된 건, Edwith 부스트코스 덕이다 ㅠ 나 왜 이제봤니.. 더 열심히해야지..
