자료구조(데이터 구조)는 컴퓨터 메모리를 더 효율적으로 관리하기 위해 새로 정의하는 구조체임.
malloc & pointer
int main(void)
{
int *x;
int *y;
x = malloc(sizeof(int));
*x = 42;
*y = 13;
}-
pointer x 에 대해서는 malloc(sizeof(int))으로 메모리 주소(공간)를 할당해줬음.
-
pointer y 에 대해서는 공간을 할당해주지 않았음.
-
pointer x가 가리키는 지점에는 42를, pointer y가 가리키는 지점에는 13을 저장해주었으나, y는 가리키는 지점이 정의가 되지 않았음.
-
이렇게 초기화 되지 않은 pointer y는 임의의 공간을 가리키고 있을 수도 있는데, 그 곳에 13이라는 값을 저장하여 오류를 발생시킬 수도 있음.
-
이를, "쓰레기값을 가진다"라고 표현함.
realloc
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
int *list = malloc(3 * sizeof(int));
if (list == NULL)
{
return 1;
}
list[0] = 1;
list[1] = 2;
list[2] = 3;
// tmp 포인터에 메모리를 할당하고 list의 값 복사
int *tmp = realloc(list, 4 * sizeof(int));
if (tmp == NULL)
{
return 1;
}
// list가 tmp와 같은 곳을 가리키도록 지정
list = tmp;
// 새로운 list의 네 번째 값 저장
list[3] = 4;
// list의 값 확인
for (int i = 0; i < 4; i++)
{
printf("%i\n", list[i]);
}
//list 의 메모리 초기화
free(list);
}-
기존에 할당된 메모리의 크기를 조절하고자 할 때, realloc을 이용하면 편하다.
-
파라미터로 변경하고자 하는 포인터, 메모리 크기를 넘겨준다.
-
realloc으로 메모리 크기를 재설정 했을 땐, 변경 전 메모리는 초기화해주지 않아도 되지만, 변경 후 메모리는 초기화를 꼭 해주도록 하자.
연결리스트(Linked lists)
-
자료 구조란, 프로그래밍 구조일 뿐이다.
-
자료 구조는, 컴퓨터 메모리에 정보를 각기 다른 방법으로 저장할 수 있도록 해줌.
-
struct : 새로운 type 설정
-
. : 속성 값 접근 (person.name -> person 타입의 name 속성에 접근)
-
* : 역참조 연산자. 메모리 덩어리로 접근하여 저장된 값 호출
-
array(배열) : 값들의 리스트를 저장할 수 있음. 단점 : "고정된 메모리 덩어리" 배열의 크기를 조절해서 더 많은 값을 넣고 싶을 때, 더 많은 메모리를 할당해야 했음. -> O(n) / 장점 : []를 이용하여 쉽게 인덱싱 할 수 있음. 빠름. 바이너리 탐색 같은 곳에 적용 가능. 인덱스 값이 메모리 상에 연이어 저장되어 있음.
-
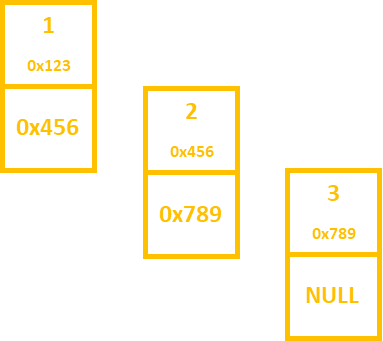
연결리스트 : 값들의 리스트를 저장하는 방법. 자신의 값과 함께 바로 다음 값의 주소(포인터)를 저장함. 숫자를 추가하기 위해서 크기를 늘리거나, 기존의 값을 이동해야 하는 번거로움이 사라짐. 주소를 가리키기만 하면 되기 때문! Dynamic! 원래 있던 것을 안 움직여도, 리스트를 늘릴 수 있음. / 단점 : 랜덤엑세스 불가 (중간의 값으로 바로 갈 수 없음) -> 바이너리 탐색 불가 -> O(n)
-
자신의 값 + 다음 값의 주소(포인터) = "Node"라고 부른다.
-
다음 값이 없는 경우, NULL(0x0)을 다음 값의 주소로 저장함.
typedef struct node // 2. 구조체 정의 시 node라는 단어를 설정해주었다.
{
int number;
struct node *next; // 1. node를 내부에서도 사용하기 위해,
}
node;- 연결리스트는 위와 같이 정의할 수 있음. number: node가 가지는 값 /*next: 다음 node를 가리키는 포인터
(*n).number = 2; // n의 메모리의 값의 number 속성에 2를 저장함.
n->number = 2; 로 바꿔서 사용 가능#include <stdio.h>
#include <stdlib.h>
// Represents a node
typedef struct node
{
int number;
struct node *next;
}
node;
int main(void)
{
// List of size 0
node *list = NULL;
// Add number to list
node *n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 1;
n->next = NULL;
list = n; // Pointing at new node (첫 번째 node의 주소)
// Add number to list
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 2;
n->next = NULL;
list->next = n; // list가 첫번째 node를 가리키고 있었으므로, 그 것의 next는 두 번째 node를 가리킨다.
// Add number to list
n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 3;
n->next = NULL;
list->next->next = n; // list->next가 두번째 node를 가리키고 있었으므로, 그 것의 next는 세 번째 node를 가리킨다.
// Print list
for (node *tmp = list; tmp != NULL; tmp = tmp->next)
{
printf("%i\n", tmp->number); // tmp가 가리키는 number 필드의 숫자를 출력
}
// Free list
while (list != NULL)
{
node *tmp = list->next;
free(list);
list = tmp;
}
}이번 내용 또한 이해하는 데 시간이 오래 걸렸다. 저 list->next->next->... 이부분이 너무 이해가 안갔기 때문이다. 주소를 따라간다는 내용이, 파이썬으로 가볍게 코딩을 시작한 나에게 너무 어려운 내용이긴했다. 앞으로 익숙해져야 하기 때문에, 어떻게든 해결을 보았다.
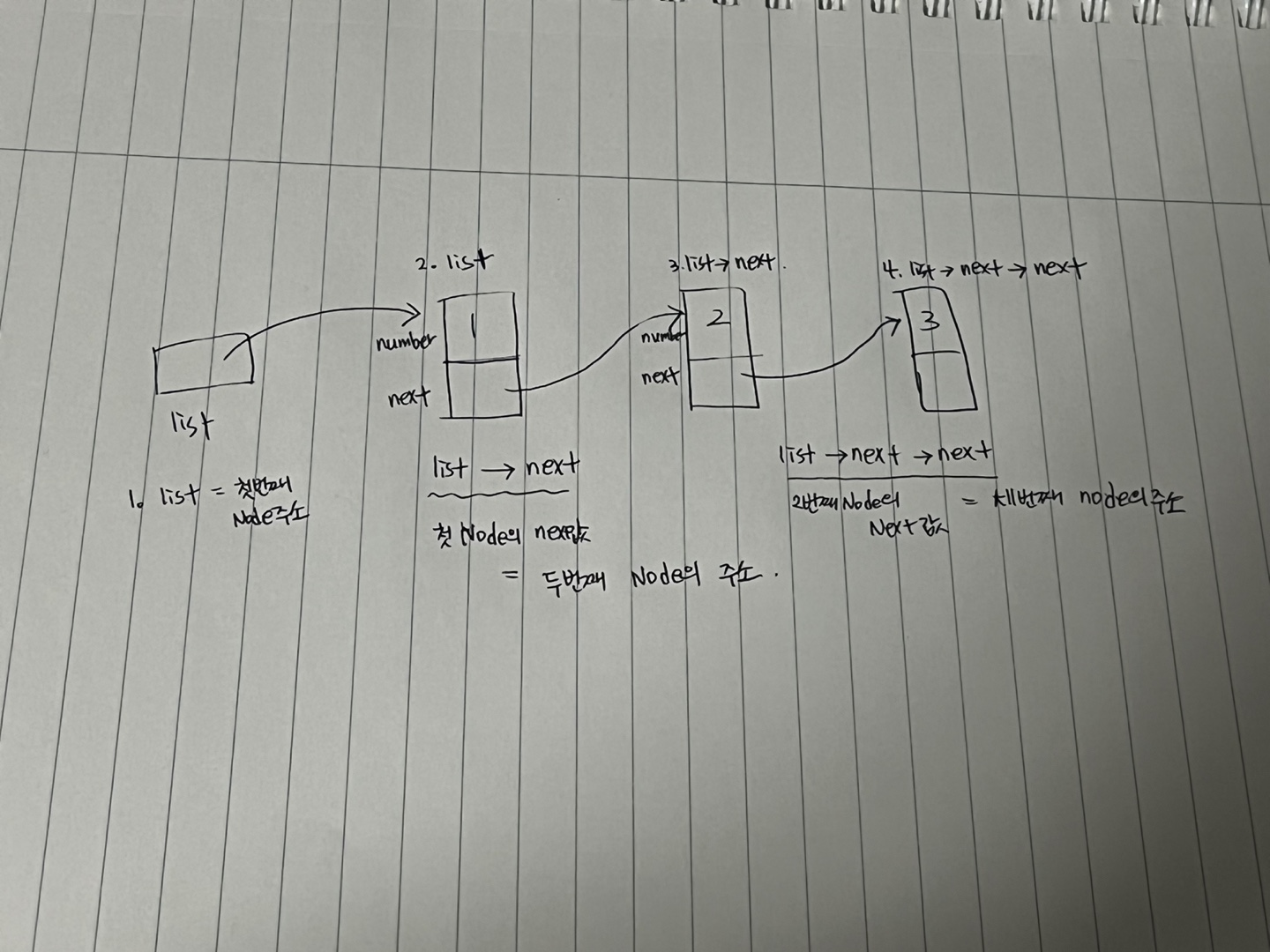
- list라는 pointer에 첫번째 node의 주소를 할당해줌으로써, 첫번째 node를 가리키게 한다.
- list->next는 첫번째 node의 next 값, 즉 두번째 node를 가리키는 포인터가 된다. 여기에 두번째 node의 주소를 할당해준다.
- list->next->next는 세번째 node를 가리키는 포인터가 된다. 어휴 C 너무 어렵다ㅠ
Binary search trees
-
각 노드들의 연결이 2차원적으로 구성 됨
-
루트 노드, 자식 노드로 구성
-
이진 검색 수행 및 노드 삽입 시 유리 : O(log n)
//이진 검색 트리의 노드 구조체
typedef struct node
{
int number;
struct node *left;
struct node *right;
} node;
// 이진 검색 함수 (node *은 이진 검색 트리를 가리키는 포인터. 변수로 tree 할당)
bool search(node *tree) // 주소를 argument로 받고 bool 값을 반환하는 함수
{
// 트리가 비어있는 경우 ‘false’를 반환하고 함수 종료
if (tree == NULL)
{
return false;
}
// 현재 노드의 값이 50보다 크면 왼쪽 노드 검색
else if (50 < tree->number)
{
return search(tree->left); // 왼쪽 노드의 주소를 search 함수에 넘겨줌
}
// 현재 노드의 값이 50보다 작으면 오른쪽 노드 검색
else if (50 > tree->number)
{
return search(tree->right); // 오른쪽 노드의 주소를 search 함수에 넘겨줌
}
// 위 모든 조건이 만족하지 않으면 노드의 값이 50이므로 ‘true’ 반환
else
{
return true;
}
}해시 테이블
- array + linked list : 즉, 연결리스트의 배열이다.
- [linked list1, linked list2, linked list3, linked list4...]
- 해시 함수가 이상적인 경우, 배열에 담긴 연결리스트 하나에는 단 하나의 값들만 있을 것이다. -> O(1)
- 최악의 경우, 단 하나의 배열에 모든 값들이 담겨서 O(n)이 될 수 있으나, 일반적으로는 최대한 많은 바구니를 만드는 해시 함수를 사용하기 때문에 거의 O(1)에 가깝다.
트라이 (retrieval의 줄임말)
-
어떤 자원을 절약하기 위해, 다른 자원을 소비하는 패턴을 가짐
-
노드가 "배열(array)"로 이루어진 트리임
-
O(1) 상수 시간이 걸리고, 메모리가 엄청 많이 든다
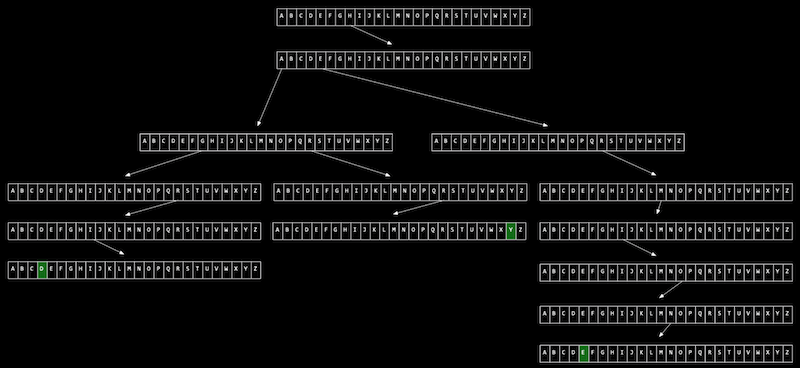 출처 : 모두를 위한 컴퓨터 과학 (CS50 2019)
출처 : 모두를 위한 컴퓨터 과학 (CS50 2019)
Queue
-
FIFO (First In First Out)
-
값이 아래로 쌓이는 구조
-
사람들이 앞으로 줄을 선 것이랑 같음
-
프린터에도 프린터 큐가 있음. (먼저 요청을 보낸 순서대로 처리)
-
enqueue : 줄에 들어가서 서는 것
-
dequeue : 줄을 빠져나오는 것
-
array & linked list : queue의 개념을 구현하기 위한 블록
Stack
-
LIFO (Last In First Out)
-
값이 위로 쌓이는 구조
-
받은 메일함 : 기본적으로 스택으로 설정되어 있음 (최근 메일이 가장 위에 있음)
-
push : stack에 어떤 element를 밀어 넣음
-
pop : 가장 위의 element를 뺌
-
array & linked list : stack의 개념을 구현하기 위한 블록
Dictionary
-
Hash table이라고도 생각할 수 있는 개념
-
key-value pair
