에라토스테네스의 체

소수 판별 알고리즘

소수를 판별하는 알고리즘은 다양한 방법이 있다.

처음 소수를 판별할때는 무지성으로 입력된 숫자에 따라 1부터 N까지 for 숫자가 나누어떨어지는지 체크를 하면서 소수를 판별할 수 있다.

하지만 이 방법은 늘 알고리즘 복잡도O(N)에 밀려서 시간초과가 뜨게 된다.

대량의 소수 판별을 하는 방법은 에라토스테네스의 체라는 알고리즘을 사용하면 O(N^1/2)로 시간초과를 파훼할 수 있다.

에라토스테네스의 체

 원리는 다음과 같다.

1. 2부터 소수를 구하고자 하는 구간의 모든 수를 나열한다. 그림에서 회색 사각형으로 두른 수들이 여기에 해당한다.
2. 2는 소수이므로 오른쪽에 2를 쓴다. (빨간색)
3. 자기 자신을 제외한 2의 배수를 모두 지운다.
4. 남아있는 수 가운데 3은 소수이므로 오른쪽에 3을 쓴다. (초록색)
5. 자기 자신을 제외한 3의 배수를 모두 지운다.
6. 남아있는 수 가운데 5는 소수이므로 오른쪽에 5를 쓴다. (파란색)
7. 자기 자신을 제외한 5의 배수를 모두 지운다.
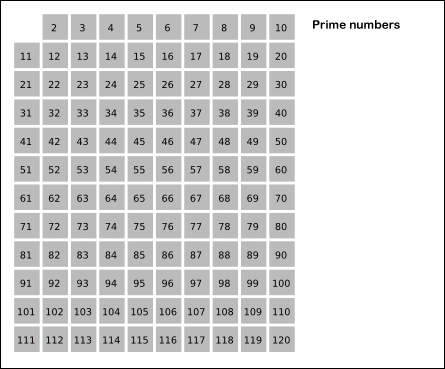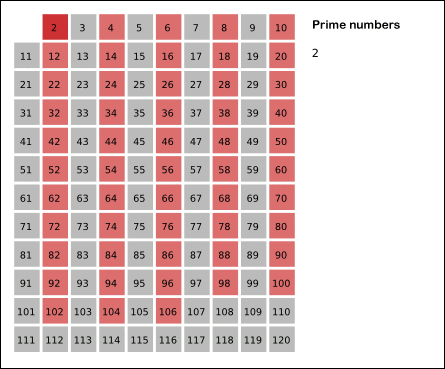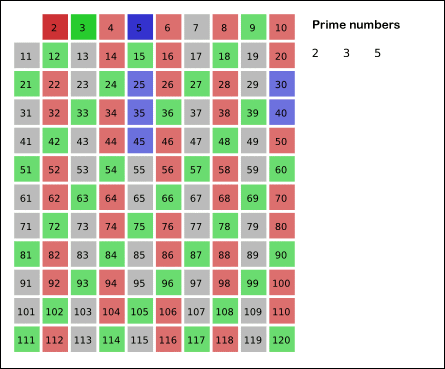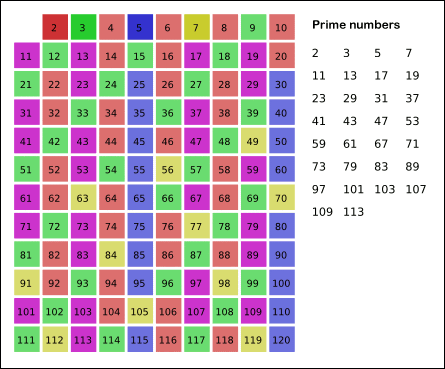
8. 남아있는 수 가운데 7은 소수이므로 오른쪽에 7을 쓴다. (노란색)
9. 자기 자신을 제외한 7의 배수를 모두 지운다.
10. 위의 과정을 반복하면 구하는 구간의 모든 소수가 남는다.

그림의 경우, 이므로 11보다 작은 수의 배수들만 지워도 충분하다. 즉, 120보다 작거나 같은 수 가운데 2, 3, 5, 7의 배수를 지우고 남는 수는 모두 소수이다.

코드로 풀면 다음과 같다.

for문을 len(temp) ** 0.5 밖에 돌리지 않기 때문에 문제의 Input이 1000000이라도 풀어낼 수 있다!

last_num = 1000000
temp = [i for i in range(last_num + 1)]

for i in range(2, int(len(temp) ** 0.5) + 1): # 2부터 제곱근(N)까지
    if temp[i] != 0: # 자기자신을 제외한 배수는 모두 0으로 초기화
        cnt = 2 # 배수를 나타낼 변수 
        while True:
            if temp[i] * cnt > last_num: # while 문을 끝낼 조건문 
              	break										 #숫자가 last num까지 다 돌았으면 종료
            else:
                temp[temp[i] * cnt] = 0 # 자기 자신을 제외한 배수는 모두 0으로 지웠음 
                cnt += 1 # 배수 count ++ 
temp[1] = 0 # temp가 0부터 시작하므로 숫자 1은 소수가 아니므로 0으로 초기화 

문제 풀어보기

https://www.acmicpc.net/problem/6588
https://www.acmicpc.net/problem/1978
https://www.acmicpc.net/problem/1929