백준 11692번 시그마 함수 문제 풀이

문제 링크 : https://www.acmicpc.net/problem/11692

풀이

약수와 관련된 문제여서 소인수분해를 해보며 접근했습니다. 약수의 합이 짝수가 되기 위해서는 약수 중 홀수의 개수가 짝수개 있어야 합니다. 대부분 학창시절 약수의 개수를 구하는 문제를 접해봤을 듯 합니다. 약수의 개수를 구하는 방법은 아래 표를 보면 유추할 수 있습니다.

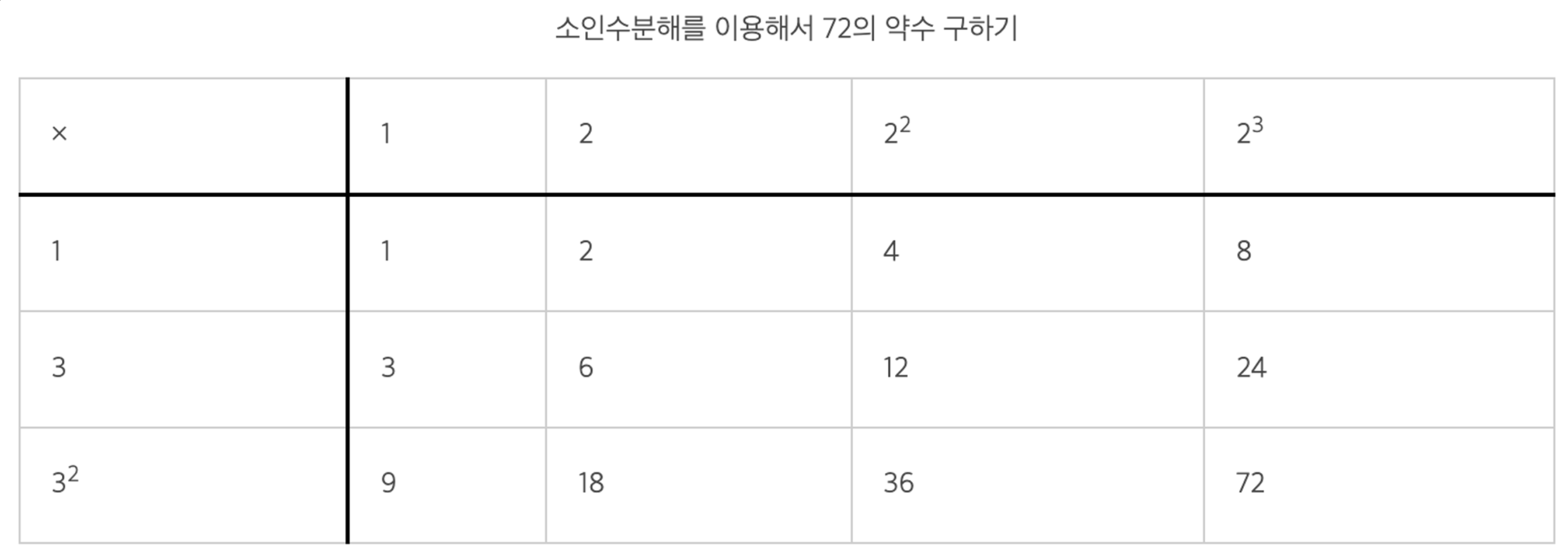
출처 : https://mathbang.net/201#gsc.tab=0

소인수분해를 하여 소수 거듭제곱들의 곱 꼴로 만들고, 지수들에 +1 한 값들을 곱하면 약수의 개수를 구할 수 있습니다. 그렇다면 약수 중 홀수인 것들의 개수는 어떻게 구할까요? 소인수분해 결과에서 홀수인 소인수들만 고려해주면 됩니다. 홀수인 소인수들의 지수에 1을 더해서 곱해주면, 홀수인 약수의 개수를 구할 수 있습니다. 예를 들면, $2^x \times 3^y \times 5^z$ 이 숫자에서는 $(y+1)(z+1)$개의 홀수인 약수가 존재합니다.

이제, 이 값(소인수분해한 결과에서 홀수인 소인수의 지수에 1을 더해서 모두 곱한 값)이 홀수가 되는 경우에 대해서 생각해봅시다. 어떤 수들을 곱해서 홀수가 되려면 어떤 수들이 전부 홀수여야 합니다.

• 홀수 x 홀수 → 홀수
• 짝수 x 홀수, 짝수 x 짝수 → 짝수

지수에 +1 해서 약수의 개수를 구하기 때문에, 홀수인 소인수들의 지수가 전부 짝수여야 한다는 뜻이 됩니다.
이말은 곧 제곱수라는 의미입니다.
예를 들면, $2^2 \times 3^2, ~ 3^4, ~2\times 3^4\times 5^2, ~3^4 \times 5^2$ 이런 수들이 있습니다.

소인수분해 결과에 2가 포함되어 있는지에 대한 여부는 시그마 함수의 값이 짝수가 되는 데에 영향을 끼치지 않습니다. 따라서 우리는 모든 제곱수를 빼주면 됩니다. 다만 소인수 2의 지수가 홀수개인지 짝수개인지 알 수 없으므로, 두 가지 경우를 모두 빼줘야합니다.

• 제곱수
• 제곱수 $\times ~2$

1~m(입력값) 사이의 제곱수의 개수는 int(sqrt(m)) 개 입니다.
제곱수 $\times ~2$ 의 개수는 int(sqrt(m/2)) 개 입니다.

최종적으로, 구하고자 하는 값은 m - int(sqrt(m)) - int(sqrt(m/2)) 으로 구할 수 있습니다.

Code

if __name__ == "__main__":
    N = int(input())
    
    print(N - int(sqrt(N)) - int(sqrt(N/2)))