[코테 문제 풀이] 백준 3665번 - 최종 순위(파이썬)

문제 링크 : https://www.acmicpc.net/problem/3665

문제 설명

올해 ACM-ICPC 대전 인터넷 예선에는 총 n개의 팀이 참가했다. 팀은 1번부터 n번까지 번호가 매겨져 있다. 놀랍게도 올해 참가하는 팀은 작년에 참가했던 팀과 동일하다.

올해는 인터넷 예선 본부에서는 최종 순위를 발표하지 않기로 했다. 그 대신에 작년에 비해서 상대적인 순위가 바뀐 팀의 목록만 발표하려고 한다. (작년에는 순위를 발표했다) 예를 들어, 작년에 팀 13이 팀 6 보다 순위가 높았는데, 올해 팀 6이 팀 13보다 순위가 높다면, (6, 13)을 발표할 것이다.

창영이는 이 정보만을 가지고 올해 최종 순위를 만들어보려고 한다. 작년 순위와 상대적인 순위가 바뀐 모든 팀의 목록이 주어졌을 때, 올해 순위를 만드는 프로그램을 작성하시오. 하지만, 본부에서 발표한 정보를 가지고 확실한 올해 순위를 만들 수 없는 경우가 있을 수도 있고, 일관성이 없는 잘못된 정보일 수도 있다. 이 두 경우도 모두 찾아내야 한다.

• 입력 조건 첫째 줄에는 테스트 케이스의 개수가 주어진다. 테스트 케이스는 100개를 넘지 않는다. 각 테스트 케이스는 다음과 같이 이루어져 있다.
  • 팀의 수 n을 포함하고 있는 한 줄. (2 ≤ n ≤ 500)
  • n개의 정수 t를 포함하고 있는 한 줄. (1 ≤ t ≤ n) t는 작년에 i등을 한 팀의 번호이다. 1등이 가장 성적이 높은 팀이다. 모든 ti는 서로 다르다.
  • 상대적인 등수가 바뀐 쌍의 수 m (0 ≤ m ≤ 25000)
  • 두 정수 a와 b를 포함하고 있는 m줄. (1 ≤ a < b ≤ n) 상대적인 등수가 바뀐 두 팀이 주어진다. 같은 쌍이 여러 번 발표되는 경우는 없다.
• 출력 각 테스트 케이스에 대해서 다음을 출력한다.
  • n개의 정수를 한 줄에 출력한다. 출력하는 숫자는 올해 순위이며, 1등팀부터 순서대로 출력한다. 만약, 확실한 순위를 찾을 수 없다면 "?"를 출력한다. 데이터에 일관성이 없어서 순위를 정할 수 없는 경우에는 "IMPOSSIBLE"을 출력한다.

입출력 예시

예제 입력 1

3
5
5 4 3 2 1
2
2 4
3 4
3
2 3 1
0
4
1 2 3 4
3
1 2
3 4
2 3

예제 출력 1

5 3 2 4 1
2 3 1
IMPOSSIBLE

문제 풀이 1.

최종 순위 문제는 2가지 방법으로 풀었다.

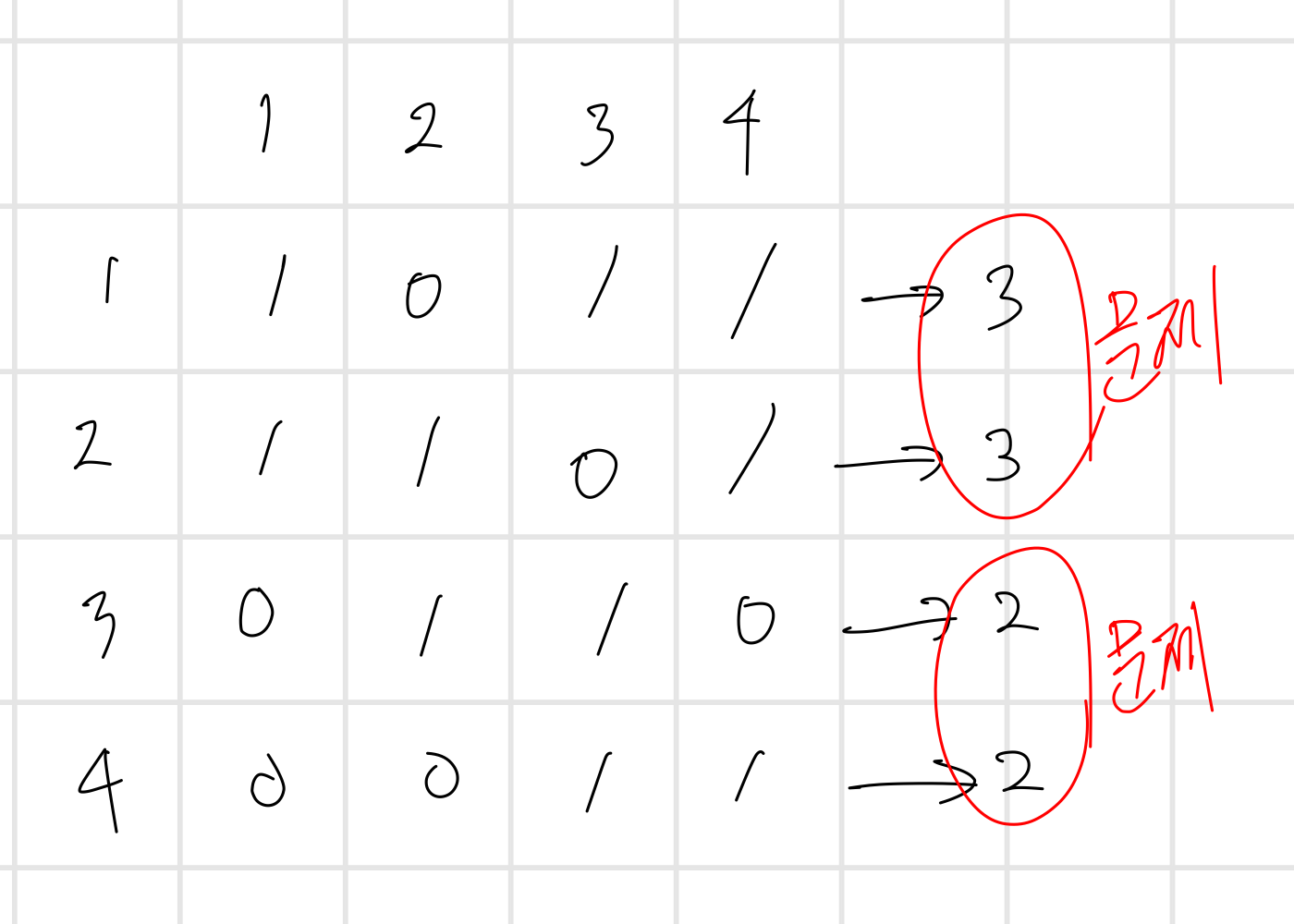
첫 번째 방법은 NxN 인접 행렬 graph를 이용한 풀이다. graph[v1][v2] 의 의미는 v1노드가 v2노드를 이길 수 있는지의 여부이다. 우선 작년 순위 rank 를 순회하면서 지면 1로 초기화되어 있는 graph[v1][v2]를 0으로 수정한다. 그리고 M개의 상대적인 등수가 바뀌는 쌍을 입력받으면서 graph에서 두 노드간의 승패 여부를 수정해준다. 최종적으로 모든 노드가 등수가 정해지려면 다음과 같이 sum(graph[i])값(1 ≤ i ≤ N)이 모두 달라야 한다.

다음과 같이 sum(graph[i])값(1 ≤ i ≤ N)이 같은 것이 생길 경우 두 노드의 등수를 특정할 수 없는 문제가 생기고, 이러한 경우 IMPOSSIBLE을 출력해야 한다.

CODE 1.

import sys
input = sys.stdin.readline
from collections import deque

def solution_1():
    T = int(input())
    for _ in range(T):
        N = int(input()) # 노드 수
        graph = [[1] * (N+1) for _ in range(N+1)] # 모든 노드가 모든 노드를 이긴다고 초기화
        rank = list(map(int, input().split())) # 인덱스 순으로 등수 나열, rank[0] -> 1등
        
        for i in range(N):
            v = rank[i] # i+1등 노드 v
            for rest_node in rank[i+1:]: # i+2등 노드부터는 v한테 짐
                graph[rest_node][v] = 0
        
        M = int(input())
        for _ in range(M):
            V1, V2 = map(int, input().split())
            tmp = graph[V1][V2]
            graph[V1][V2] = graph[V2][V1]
            graph[V2][V1] = tmp
        
        can_rank = [False] * (N+1)
        answer = [0] * N
        for v, g in enumerate(graph): # v는 노드 번호, sum(g)는 이긴 횟수, N-이긴횟수 = answer 인덱스
            if v == 0:
                continue
            g = g[1:]
            s = sum(g)
            can_rank[s] = True
            i = N-s
            answer[i] = v
        
        # print(f'can_rank : {can_rank}')
        if False in can_rank[1:]:
            print("IMPOSSIBLE")
        else:
            for v in answer:
                print(v, end=' ')
            print()

if __name__ == "__main__":
    solution_1()
    # solution_2() # 위상 정렬 사용한 풀이 
    

시간 복잡도

문제 풀이 2.

두 번째 방법은 위상 정렬을 이용한 풀이이다. v1 노드가 v2 노드를 이긴다는 것을 v1→v2 로 해석하여, 인접 리스트 graph와 indegree 배열을 만든다. 이 뒤로는 위상 정렬의 핵심 알고리즘대로 코드를 구현한다.

CODE 2. 위상 정렬 사용

import sys
input = sys.stdin.readline
from collections import deque

def solution_2():
    '''
        위상 정렬을 사용항 코드
        - 인덱스는 노드, 값은 해당 노드의 진입차수를 저장하는 indegree 배열을 사용
        - 핵심 알고리즘
            1. 진입 차수가 0인 노드를 큐에 넣는다
            2. 큐가 빌 때까지 다음의 과정을 반복한다.
                2-1. 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다.
                2-2. 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.
    '''
    T = int(input())
    for _ in range(T):
        N = int(input()) # 노드 수
        graph = [[] for _ in range(N+1)]
        rank = list(map(int, input().split())) # 인덱스 순으로 등수 나열, rank[0] -> 1등
        
        # 1. 위상 정렬을 위한 indegree 생성
        indegree = [0] * (N+1)
        
        # 등수에 따라 간선 생성, 5번이 1번 이기면 5->1 간선 생성
        lose_nodes = [i for i in range(1, N+1)]
        for win in rank: # 등수별로 v 나옴
            lose_nodes.remove(win)
            # 남은 노드는 다 이기는걸로 간주
            for lose in lose_nodes:
                graph[win].append(lose)
                indegree[lose] += 1
        
        M = int(input())
        for _ in range(M):
            V1, V2 = map(int, input().split())
            if V2 in graph[V1]: # V1->V2 를 V2->V1 으로 바꿔줌
                graph[V1].remove(V2)
                graph[V2].append(V1)
                indegree[V1] += 1
                indegree[V2] -= 1
            else:
                graph[V2].remove(V1)
                graph[V1].append(V2)
                indegree[V1] -= 1
                indegree[V2] += 1
        
        # 2. indegree 값이 0인 노드 큐에 추가
        queue = deque([])
        for v in range(1, N+1):
            if indegree[v] == 0:
                queue.append(v)
        
        # 3. 큐가 빌 때 까지, 
        answer = []
        while queue:
            v1 = queue.popleft()
            answer.append(v1)
            # 3-1. v1에서 나가는 간선 그래프에서 제거 + 진입차수 0인 노드 큐에 추가
            for v2 in graph[v1]:
                indegree[v2] -= 1
                if indegree[v2] == 0:
                    queue.append(v2)
        # 4. 큐가 비었는데 간선이 남아있는 경우 impossible
        if any(indegree):
            print("IMPOSSIBLE")
        else:
            for v in answer:
                print(v, end=' ')
            print()

if __name__ == "__main__":
    # solution_1()
    solution_2() # 위상 정렬 사용한 풀이 
    

시간 복잡도

• (2 ≤ N ≤ 500)
• E = N(N+1)/2
• (0 ≤ M ≤ 25000)

1. 간선 정보 생성 및 진입 차수 계산: O(N^2) - 순위 정보를 바탕으로 간선 정보를 생성하고, 진입 차수를 설정한다.
2. M번의 상대적인 등수가 바뀐 쌍 처리: O(M) - 경기 결과를 반영하여 간선의 방향을 바꾸고, 진입 차수를 업데이트한다.
3. 위상 정렬 실행: O(N+E) - 모든 노드를 큐에 넣고, 각 노드에서 출발하는 간선을 제거하면서 위상 정렬을 수행한다. 여기서 E는 간선의 총 개수이다. E는 N(N-1)/2이 될 수 있으므로, 이 단계의 시간 복잡도는 O(N^2)으로 볼 수 있다.