[알고리즘] 1주차 스택, 큐, 우선순위 큐

스택

• 제한적 접근 : 한쪽 끝에서만 자료 관리
• LIFO : 나중에 들어온 게 가장 먼저 나가는 데이터 구조

구조

• LIFO, FILO

• 대표적 활용 : CPU의 프로세스 구조 함수 동작 방식

• 추상 자료형 ADT

  • push : 맨 위 항목 삽입
  • pop : 맨 위 항목 삭제
  • top : 스택 맨 위를 표시
  • isEmpty : 비었는지 확인
  • isFull : 가득 차 있는지 확인
  • getSize : 갖고 있는 element 수 반환

• 주 기능

  • push : 데이터 넣기
    1. isFull?
    1. true : 오류 발생 및 종료
    2. ++top
       1. top 위치에 데이터 추가
  • pop : 꺼내기
  1. isEmpty?
     1. true : 오류 발생 및 종료
     2. top이 가리키는 데이터 삭제
        1. --top
        2. return 성공 / 삭제한 데이터 반환

특징

• 장점
  • 속도가 빠르다
  • 구조가 단순해 구현 쉽다
• 단점
  • 저장 공간 낭비 : 미리 확보해야 함
  • 최대 개수 정해야 함

구현

• Array
  • 장점
    • 접근 속도가 빠름
      • 구현 쉬움
  • 단점
    • 변경이 용이하지 않음
      • 크기가 동적이 아님
  • 검색이 많을 때 사용
• Linked List
  • 장점
    • 변경 용이 : 메모리 주소만 변경하면 됨
      • 크기가 동적임
  • 단점
    • 접근 어려움 : 연속된 공간이 아니기 때문에
      • 포인터를 위한 추가 메모리 공간 필요
  • 변경이 많을 때 사용

Time Complexity

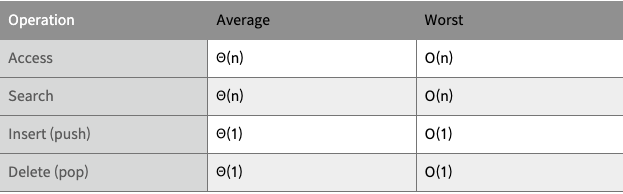
큐

• 줄 서는 구조
• FIFO : 가장 먼저 넣은 데이터를 가장 먼저 꺼내기

구조

• FIFO, LILO
• 대표 활용 : Multi Tasking을 위한 프로세스 스케줄링 방식 구현에 사용
• 추상 자료형 ADT
  • enqueue : end에 항목 추가
  • dequeue : front 항목 제거
  • peek : front 반환
  • isFull : 가득 차있는지 확인
  • isEmpty : 비어있는지 확인
• 주 기능
  • enqueue : 데이터 end에 넣기
    list.append(data)
  • dequeue : 꺼내기
    1. data = list[0]
    2. del list[0]
    3. return data

특징

• 장점
  • 입력 데이터 순서 정하는데 최적화
• 특정 상태에 따라 우선순위 결정하기도 함 (:우선순위 큐)
• end----front 형태

구현

• Array
  • 장점
    • 구현 쉬움
  • 단점
    • 변경이 용이하지 않음
    • 크기가 동적이 아님
  • 검색이 많을 때 사용
• Linked List
  • 장점
    • 변경 용이 : 메모리 주소만 변경하면 됨
    • 크기가 동적임
  • 단점
    • 포인터를 위한 추가 메모리 공간 필요
  • 변경이 많을 때 사용

종류

• 선형 큐 Linear Queue
  • 기본적인 큐 형태 (막대)
  • 단점
    • enqueue,dequeue가 많은 경우 비어있어도 자료 삽입 불가 경우 있음
    • 자료 위치 변경 어려움..
• 환형 큐 Circular Queue
  선형 큐의 단점 보완
  • 배열의 처음과 끝을 연결해 원형으로 구성
  • 빈 공간 없이 front,end를 옮기면 됨

Time Complexity

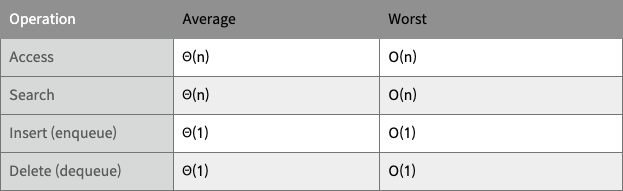
우선순위 큐

• 들어간 순서에 상관없이 우선순위가 높은 데이터가 먼저 나오는 큐

구조

• 힙 이용
  • 완전 이진 트리
  • 모든 노드에 저장된 값인 우선순위는 자식 노드의 값보다 크거나 같다.
  • 루트 노드에 우선순위가 가장 높은 데이터를 위치시키는 자료구조가 된다.
  • 힙에서 노드를 뺄 때마다 우선 순위가 높은 데이터가 먼저 나옴
• 추상 자료형 ADT
  • Insert : item 삽입
  • Remove : 가장 우선순위가 높은 요소 삭제 및 반환
  • Find : 우선순위 가장 높은 요소 반환
  • Empty : 공백 상태인지 확인
  • Full : 포화 상태인지 검사
  • Display : 모든 요소 출력
• 주기능
  • 데이터 저장
    1. input이 들어옴. 우선순위 낮다고 가정하고 맨 끝에 저장
       ➡️ 저장 보다는 부모 노드가 될 것과 비교만 하는 편이 좋음
    2. 부모 노드와 우선순위를 비교해서 자식이 크면 자리를 바꾸면서 최소 힙의 구조를 유지할 때까지 반복
  • 데이터 삭제
    1. 힙의 루트 노드 반환 : 가장 우선순위가 높은 데이터를 빼는 것이므로
    2. 루트 노드 삭제 이후 힙의 구조 그대로 유지하기 (=heapify 과정)
       1. 루트 노드 반환 후 마지막 노드를 루트 노드로 옮기기
       2. 자식 노드와 우선순위를 비교하여 자리를 바꾸면서 최소 힙의 구조를 유지할 때까지 반복
          ➡️ 새로운 요소가 자식 노드들 보다 값이 크면 더 이상 교환 필요 없다.

구현

• 힙
  • 삭제, 삽입 과정 모두 부모와 자식 간의 비교만 이루어진다.
  • 삭제: O(log2n), 삽입: O(log2n)
  • 힙 구현은 배열로! : 직관적이고 다루기 용이함
• 배열이나 연결리스트로 구현하지 않는 이유?
  우선순위를 매기면서 중간에 들어가야 하는 것이 생기면 삽입 과정이 복잡해진다. 최악의 경우 모든 인덱스를 탐색할 수도 있다. (삭제: O(1), 삽입: O(n))

Time Complexity

• 트리 높이 : log2n
• 삽입 : O(log2n)
  ➡️ 최악 : 새로운 요소가 부모와의 비교 과정에서 루트노드까지 올라갈 경우, 트리의 높이 만큼의 비교 및 이동 연산이 필요하다.
• 삭제 : O(log2n)
  ➡️ 최악 : 마지막 노드가 루트 노드로 올라오고 난 후 자식과 비교 과정에서 마지막 레벨까지 내려갈 경우, 트리의 높이 만큼의 시간이 필요

참고
스택

• https://yoongrammer.tistory.com/45
• https://cloudstudying.kr/lectures/141

큐

• https://yoongrammer.tistory.com/46
• https://cloudstudying.kr/lectures/142

우선순위 큐

• https://chanhuiseok.github.io/posts/ds-4/
• https://euncero.tistory.com/135