알고리즘 문제를 풀면서 시간복잡도라는 개념이 등장했다.
Time Complexity(시간복잡도)
시간복잡도란 입력값의 변화에 따라 연산을 실행할 때 연산 횟수에 비해 시간이 얼마나 걸리느냐를 나타내는 말이다.
우리가 어떠한 계산을 할 때 문제를 푸는 방법을 알고리즘이라고 한다. 이 알고리즘의 로직을 코드로 구현할 경우 단순한 계산에서는 시간이 그리 오래 걸리지 않을 것이다. 그러나, 알고리즘의 입력값이 점점 커질 경우엔 어떻게 될까? 아무리 컴퓨터의 성능이 좋다고 해도 입력값이 커질 수록 시간은 오래 걸릴 수 밖에 없을 것이다. 그렇다면 우리는 이 시간을 최대한 줄여서 코드를 작성해야 좋은 알고리즘이라고 말할 수 있다. 이 때 걸리는 시간을 나타내는 용어가 바로 시간복잡도이다. 그리고 이러한 시간복잡도는 주로 빅-오 표기법을 사용해 나타낸다.
Big-O 표기법
빅오 표기법은 최악의 경우를 고려한다. 즉 빅오 표기법으로 표기한 시간은 우리가 상정할 수 있는 최대의 시간이 걸림을 뜻한다. 그렇기에 우리는 그 시간이 걸리지 않게 좀더 효율적인 방법을 생각해 내야한다. 그렇다면 왜 최선의 경우를 고려하지 않는 것일까. 이유는 간단하다. 우리가 최선의 경우를 상정해 시간을 표기한다면 우리가 짠 코드에서 문제가 발생할 경우 어디에서 문제가 발생했는지 찾기 쉽지 않기 때문이다. 코드를 전체적으로 다 살펴야 문제를 찾을 수 있을 것이다. 하지만 최악의 상황인 경우 모든 상황에 대처가 가능하다. 우리가 현실에서도 최악인 경우를 가정한다면 어떤 일이 발생했을 때 놀라지 않고 모든 상황에 대처가 가능한 경우와 비슷하다고 할 수 있다.
시간복잡도에는 결국 알고리즘의 성능을 의미한다. 다른 의미로는 알고리즘을 수행하기 위해 컴퓨터가 수행해야되는 연산을 수치화 한 것이다.
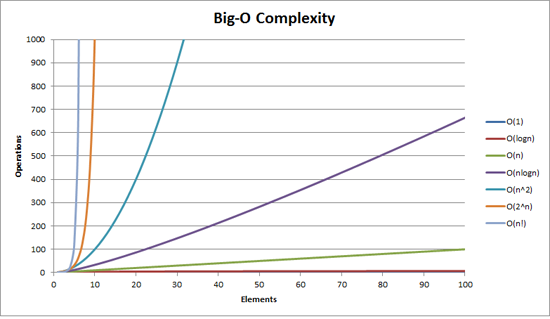
다음 그래프에서 나타낸 것과 같이 빅오 표기법은 O(n)을 이용해 나타낸다. 이때 가장 중요한 것은 n이 어디에 영향을 미치는가 이다.
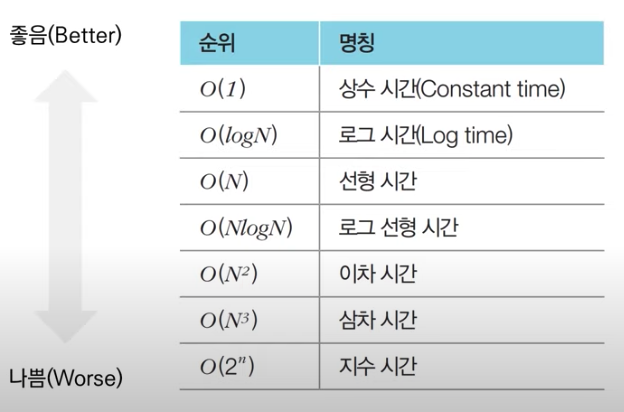
위의 표에서와 같이 n의값이 지수에 붙을 경우 가장 성능이 나쁨을 나타내고 있다. 즉 n의 값이 점점 커질 수록 연산 횟수가 기하급수적으로 늘어난다고 할 수 있다.
단순하게 말하자면 우리가 가장 많이 사용하는 반복문인 for문을 1번 쓴다고 했을 때 n은 1이다. 바깥쪽에서 for문을 2번 사용하면 n은 2n이 된다. 그러나 for문 안에 for문을 사용한 2중 for문은 n^2이 된다. 즉 반복의 반복이 되면 알고리즘은 더 많은 연산을 요구한다. n의 앞에 붙는 상수는 사실상 큰 의미가 없다. n 이나 2n이나 3n이나 시간 복잡도는 큰 차이가 없다. 단, n의 지수에 붙는 숫자는 커질 수록 입력값에 따라 그 수가 기하급수적으로 증가한다는 것을 명심해야 한다.
알고리즘 문제를 처음 풀었을 때 단순히 문제만 해결하면 된다고 생각했다. 그러나 뒤로 갈 수록 효율성 테스트에서 자꾸 실패하는 경험을 하면서 시간복잡도에 대한 생각을 해야겠다고 느꼈다. 문제를 푸는 것도 중요하지만 결국 알고리즘을 잘 한다는 것은 문제를 효과적으로 잘 푼다는 것이라는 걸 느꼈다.