item과 item 간의 연결 관계를 표현한다.

---

구성

정점 vertex

• 그래프의 구성요소
• node

간선 edge

• 두 정점을 연결하는 선

차수 degree

• 간선의 수

성질

• 정점의 수 $V$, 간선의 수 $E$에 대해 무방향 그래프는 최대 $\displaystyle{\frac{V(V-1)}{2}}$개의 간선을 가질 수 있다.
• $N:N$ 관계를 갖는 원소를 표현할 때 좋다.
  (선형 자료구조, tree로는 표현이 어렵다.)

종류

무방향 그래프 undirected graph

• A에서 B로 가는 것과 B에서 A로 가는 것을 같은 것으로 본다.
  이런 관점에서는 방향이라는 개념이 없다는 의미에서 무방향 그래프 undirected graph라 한다.
• A에서 B로도 갈 수 있고 B에서 A로도 갈 수 있다는 의미에서 양방향 그래프 bidirected graph라고도 한다.

방향 그래프 directed graph

• A에서 B로 가는 것과 B에서 A로 가는 것을 서로 다른 것으로 본다.
• 사이클이 없는 경우를 특별히 사이클이 없는 방향 그래프 DAG; Directed Acyclic Graph라 한다.

가중치 그래프 weighted graph

• 간선의 거리, 비용, etc.

완전 그래프 complete graph

• 모든 정점($V$)에 대해 가능한 모든 간선($V-1$)을 갖는 그래프

부분 그래프 sub graph

• 원래 그래프에서 떼어낸 그래프

트리도 그래프다.

• 각 노드는 최대 하나의 부모 노드가 존재할 수 있다.
• 각 노드는 자식노드를 갖지 않을 수도, 하나를 가질 수도, 여러 개를 가질 수도 있다.
• 두 노드 사이에는 유일한 경로가 존재한다.

사이클 없는 무방향 그래프는 왜 없음?

• 그냥 왔다갔다 하니까 필연적으로 사이클이 생김

최단 경로

가중치가 있다면

• 가중치 합을 최소로 하는 경로
• Dijkstra

가중치가 없다면

• 간선 수를 최소로 하는 경로
• Bellman-Ford
• BFS

표현

정점 중심

• 인접 행렬 adjacent matrix
  • $V\times V$ 크기
• 인접 리스트 adjacent list
  • 각 정점마다 다른 정점으로 ****나가는**** 간선의 정보를 저장한다.

간선 중심

• 간선 리스트 edge list

인접 행렬

• $V \times V$ spuare matrix
• 행 번호와 열 번호는 그래프의 정점에 대응된다.
• 정점 $i$와 정점 $j$가 연결되어 있으면 $a[i][j]=1$, 아니면 $0$

무방향 그래프

• $i$행의 합 = $i$열의 합 = $V_i$의 차수
• 무방향에서는 나가는 간선과 들어오는 간선의 구분이 없어서 그냥 차수라고 하는 게 보통이다.
• 그래서 대각 행렬이 된다($a[i][j]=1$이면 $a[j][i]=1$이니까).

import java.util.*;

public class AdjMatrixTest {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int v = sc.nextInt();
        int e = sc.nextInt();
        
        int[][] adjMatrix = new int[v][v];

        for(int i = 0; i < e; ++i) {
            int from = sc.nextInt();
            int to = sc.nextInt();
            adjMatrix[from][to] = adjMatrix[to][from] = 1;
        }
        
        for(int[] row : adjMatrix) {
            System.out.println(Arrays.toString(row));
        }
        
        sc.close();
    }

}

방향 그래프

• $i$ 행의 합 = $V_i$에서 나가는 간선 수(차수)
• $i$ 열의 합 = $V_i$로 들어오는 간선 수

단점

• sparse graph
  • 공간 낭비가 심하다.
  • 간선이 $8$개여도 정점이 $7$개라면 $7^2=49$개의 요소가 필요하다.
  • 탐색 효율도 낮아진다. → 인접 리스트를 쓰자
  • 그렇다고 인접 행렬을 아예 안 쓰는 건 아니고, dense graph면 쓸 만 하다.
    • 일단 구현도 쉽고 배열이라 접근 속도도 빠르기 때문에 인접 행렬이 더 좋은 경우도 있다.

인접 리스트

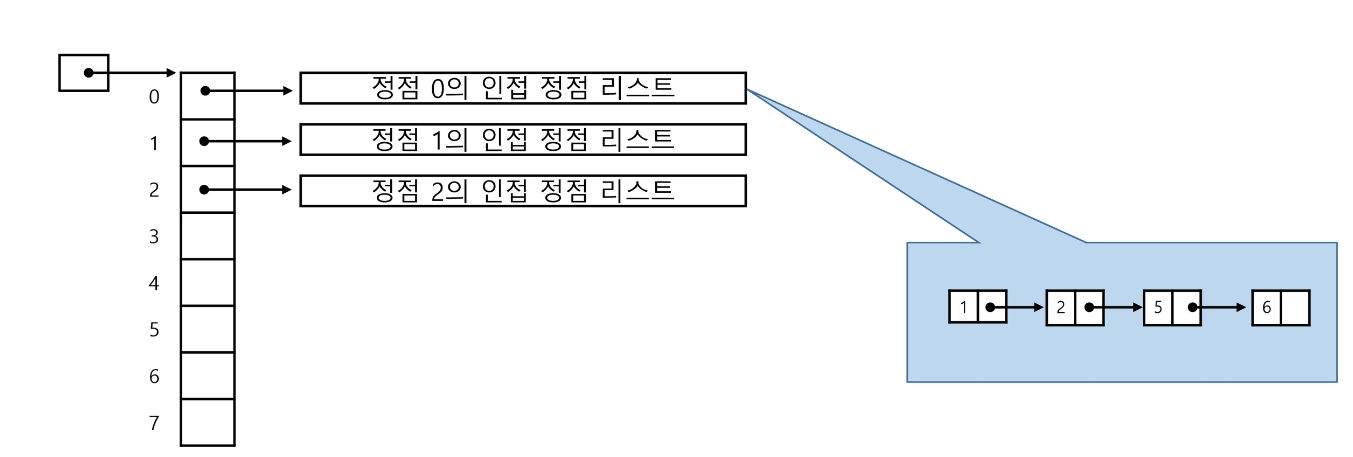
• 하나의 정점에 대한 인접 정점을 순차적으로 표현한다.

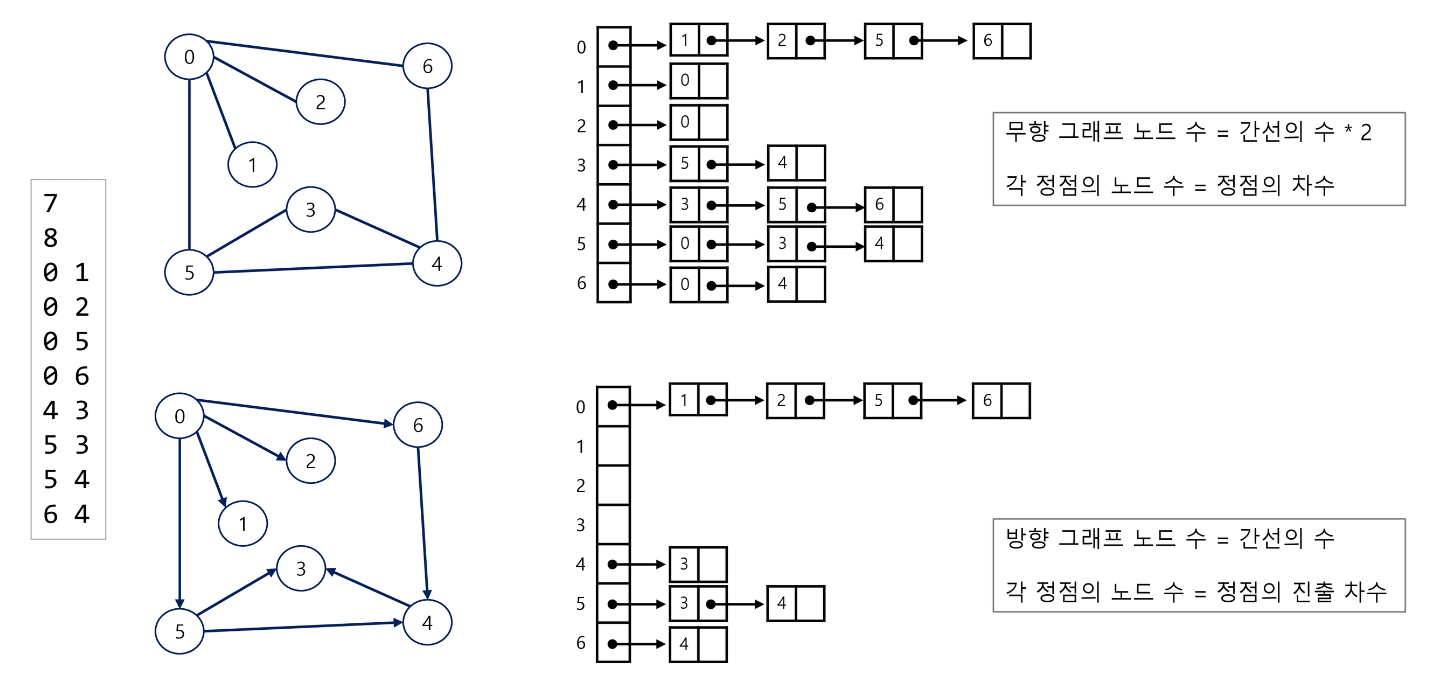
입력

7
8
0 1
0 2
0 5
0 6
4 3
5 3
5 4
6 4

이렇게 들어오는 경우는 인접 행렬보다는 인접 리스트나 간선 리스트를 노린 문제인 경우가 많음

Example

import java.util.*;

public class AdjListTest {
    static class Node {
        int vertex;
        Node next;
        
        public Node(int vertex, Node next) {
            this.vertex = vertex;
            this.next = next;
        }

        @Override
        public String toString() {
            return "Node [vertex=" + vertex + ", next=" + next + "]";
        }
    }

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int v = sc.nextInt();
        int e = sc.nextInt();
        
        Node[] adjList = new Node[v]; //사실상 헤드리스트

        for(int i = 0; i < e; ++i) {
            int from = sc.nextInt();
            int to = sc.nextInt();
            
            //이렇게 하는 이유는 인접 리스트의 순서는 무의미하기 때문
            //그냥 어느 정점과 연결되어있는지만 나타내면 된다.
            adjList[from] = new Node(to, adjList[from]);
            adjList[to] = new Node(from, adjList[to]);
        }
        for(Node node : adjList) {
            System.out.println(node);
        }

        sc.close();
    }

}

Node [vertex=6, next=Node [vertex=5, next=Node [vertex=2, next=Node [vertex=1, next=null]]]]
Node [vertex=0, next=null]
Node [vertex=0, next=null]
Node [vertex=5, next=Node [vertex=4, next=null]]
Node [vertex=6, next=Node [vertex=5, next=Node [vertex=3, next=null]]]
Node [vertex=4, next=Node [vertex=3, next=Node [vertex=0, next=null]]]
Node [vertex=4, next=Node [vertex=0, next=null]]

• adjList[i]
  • 정점 $i$에 연결된 정점들의 linked list
  • 의 head
  • 따라서 adjList는 사실상 head list가 된다.
• 재귀 호출처럼 보이는 건

  public String toString() {
      return "Node [vertex=" + vertex + ", next=" + next.toString() + "]";
  }

  사실상 이런 형태이기 때문