이번엔 투 포인터에 대해 글을 써보려 한다.
되게 쉽고 얼마되지 않는 분량이기에 가볍게 읽고 넘어가기 좋은 알고리즘이라고 생각한다.
📘 그냥 투(2) 포인트(가리키다)
대개 알고리즘은 이름 그 자체가 알고리즘의 동작과 연관되어 있는 게 큰데 투 포인터의 경우도 동일하다.
하나의 긴 배열이 있다고 가정했을 때, 그 배열에서 배열의 처음을 가리키는 포인터가 2개가 있고 이 중 포인터 하나를 좌측에서 우측으로 점차 이동시켜 원하는 결과값을 얻어내는 알고리즘이기 때문이다.
그렇기 때문에 최악의 경우(원하는 결과값이 배열의 가장 끝에 있고, 구하려는 값 또한 동일해야하는 경우)에도 O(2n)인 짧은 시간 복잡도를 가진다.
하지만 두 포인터의 이동을 통해 부분 배열을 찾아내는 데에 사용하기 때문에 대개 전체 배열에서 부분 배열의 합을 구하기 위해 사용하거나 조건을 만족하는 특정 수열을 찾기 위해서 사용한다.
📘 기본 원리
먼저 부분 배열의 값이 6을 넘는 경우의 수를 구해야한다고 가정해보겠다.
n의 길이를 가진 1차원 배열이 있고, 결과값을 담을 count 변수를 지정해주었다.
여기서 투 포인터 알고리즘을 통해 문제를 풀기 위해선 아래와 같이 몇 가지를 지정해주어야한다.
- 2개의 포인터를 지정한다.
- left : right 위치 대비 좌측에 존재한다, 이동 순서가 낮다.
- right : left 위치 대비 우측에 존재하며, 이동 순서가 높다.
- left <= right 상태를 유지해야한다.
- 처음 left, right의 값은 0이며, 이 상태에선 아무것도 더하지 않은 초기 상태이다.
- 부분합을 구할 때, left는 배열의 시작을. right는 배열의 끝을 가리킨다.
- 부분합을 구할 때에만 유효하다.(부분합이 아닌 문제이지만 알고리즘 사용이 가능한 문제 : Valid palindrome)
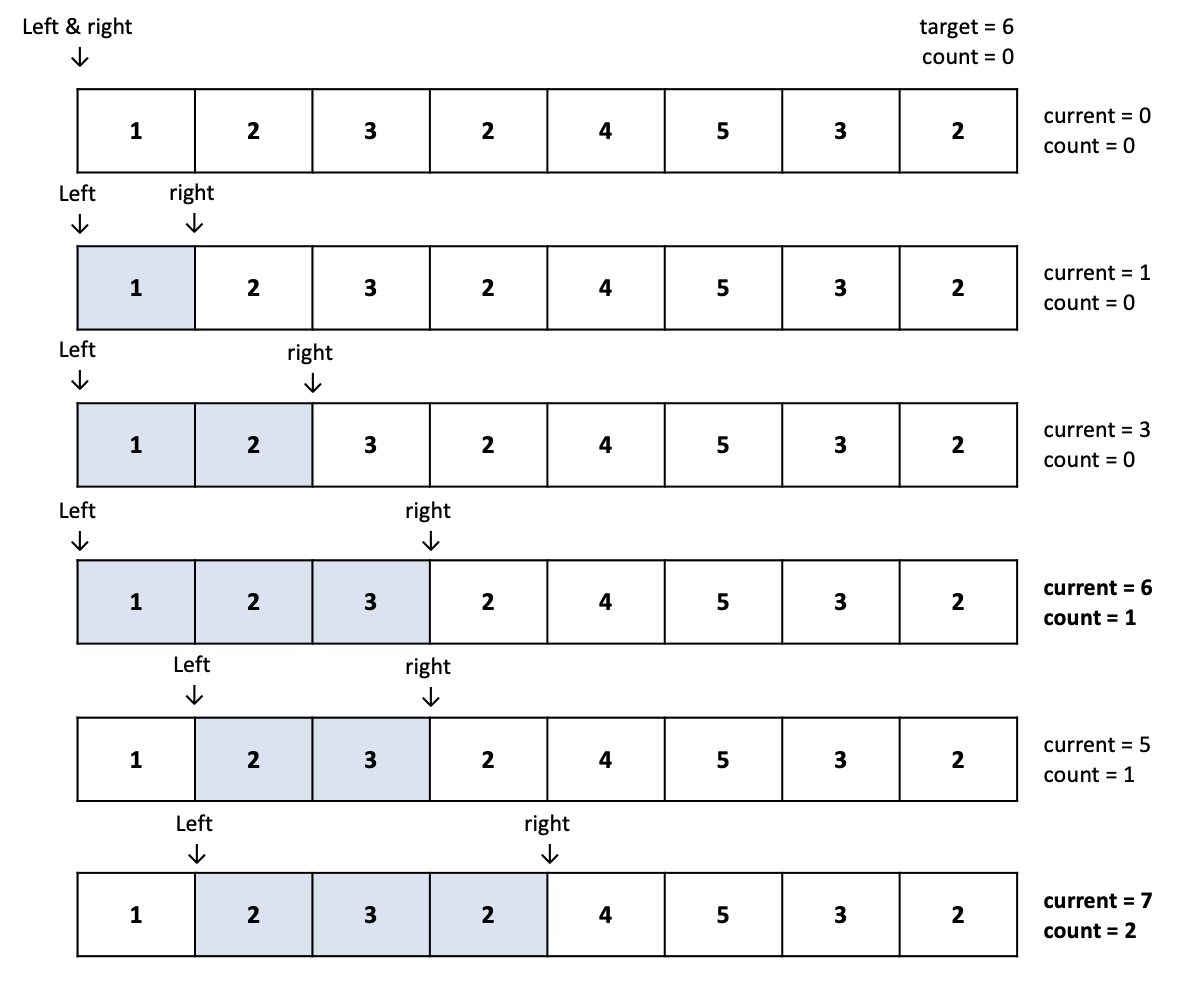
위의 그림과 같이 target = 6 이라는 상황을 가정했을 때,
target 값을 넘는 부분합의 경우의 수를 계산하는 알고리즘을 작성해보았다.
1. left, right 변수를 생성 후 배열의 가장 앞에 위치한다. (left 및 right 초기값 : 0)
2. 부분 배열의 길이를 +1 증가 시킨다. (right+=1)
3. 부분 배열의 합을 구한 후 target 값과 비교한다.
3-1. target > patial_arr 경우, right 값을 +1 증가 시킨다.
3-2. target <= patial_arr 경우, count와 left의 값을 +1 증가 시킨다.
4. left의 위치가 배열의 끝에 다다르면 반복을 종료하고 결과값을 반환한다.합을 구할 부분 배열의 위치의 시작과 끝을 각각 left, right 변수가 지정하고 있으며,
부분 배열인 patial_arr 의 값이 target 값보다 적은 경우, right+1 을 하여 배열의 부분합을 점차적으로 늘렸다.
이후, patial_arr 의 값이 target 값과 동일하거나 넘어가는 경우 count+1 을 하여 결과를 반영해주고 left+1 을 하여 다음 경우의 수를 계속하여 탐색해 나가도록 작성해보았다.
target 값이 9인 이러한 설명을 반영한 코드는 아래와 같다.
💻 Main
class Solution:
def twoPointer(self, arr:list[int], target:int) -> int:
length = len(arr)-1 # 전체 길이에서 -1하여 최종 도달 가능한 인덱스를 지정.
left, right = 0, 0 # 배열의 최좌측인 left와 우측으로 계속해서 이동할 right 변수 선언.
result = []
while left != length: # left 값이 배열의 맨 끝에 다다르면 반복 종료.
if left == 0 and right ==0: # 반복이 처음일 때, right의 값을 증가시켜 반복을 시작함.
right += 1
if sum(arr[left:right]) >= target: # 부분 배열의 합이 target 값보다 크거나 같으면
result.append(arr[left:right]) # 결과값에 해당 배열을 넣고
left += 1 # left+1 을 함으로써 다음 값의 최소 길이 부분합을 찾기 위해 이동.
if sum(arr[left:right]) < target: # 부분 배열의 합이 target 값보다 작으면
if right == length: # right의 위치가 배열의 맨 끝일 때,
left += 1 # right의 위치는 보존. left+1
else:
right += 1 # right의 위치가 배열의 맨 끝이 아닐 때, right+1
return result # 각각 최소 길이의 부분 배열을 담은 결과값을 리턴
test = Solution()
test.twoPointer([1,2,3,4,5,6,5,4,3,2,1],9)
# result = [[1, 2, 3, 4], [2, 3, 4], [3, 4, 5], [4, 5], [5, 6], [6, 5], [5, 4], [4, 3, 2]]