[ Heap ] Max Heap과 Min Heap

2학년때 배웠던 MAX-HEAP, MIN-HEAP.. 다 까먹었다. 고로 정리한다.

Perfect Binary Tree

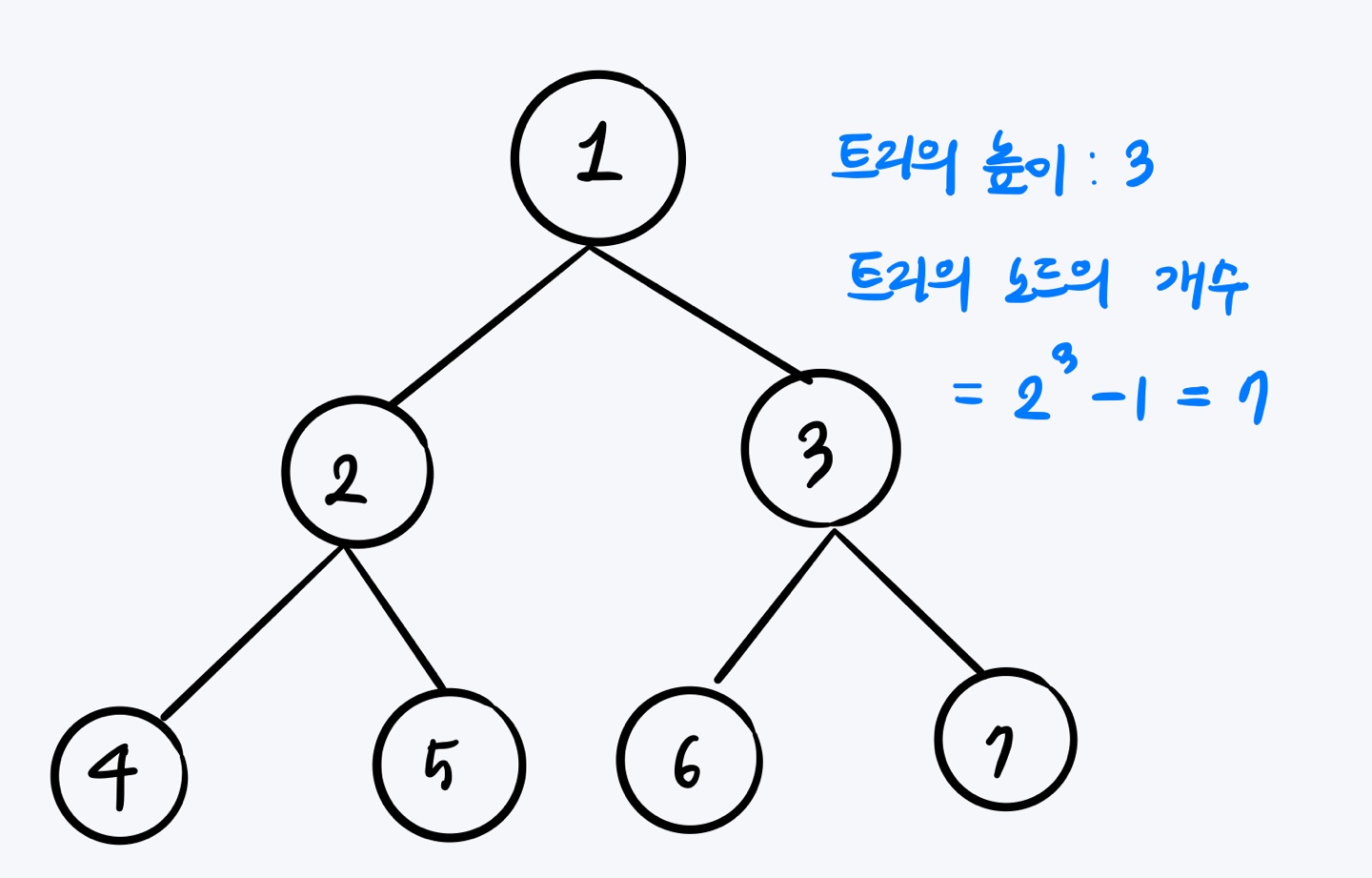
포화 이진 트리는 leaf node를 제외한 모든 노드의 자식의 수가 두개인 트리이다. leaf node는 당연히 자식의 수가 0개이다.

또한, 모든 leaf node의 depth가 같아야 한다.

그냥 한마디로 말하자면 어디 하나 구멍난 것 없이 차곡차곡 잘 채워진 이진 트리를 말한다. perfect 이진트리....

모든 leaf node의 depth가 같은 조건 덕분에, 높이가 h인 트리의 전체 노드 개수는 $2^{h-1}$개 이다.

Complete Binary Tree

Perfect Binary Tree보다 영역(?)이 넓은 트리이다. 얘는 완전 이진 트리라고 한국어로 말한다. 그냥 영어로 구분하기로 하자

Perfect Binary Tree와 같이, leaf node를 제외한 모든 노드의 자식의 수는 두개이다. 마찬가지로 leaf node는 당연히 자식의 수가 0개이다.

Perfect Binary Tree는 마지막 레벨의 노드까지 꽉꽉 차 있었다면, Complete Binary Tree의 마지막 레벨의 노드는 오른쪽부터 차례로 몇개가 없을 수도 있다.

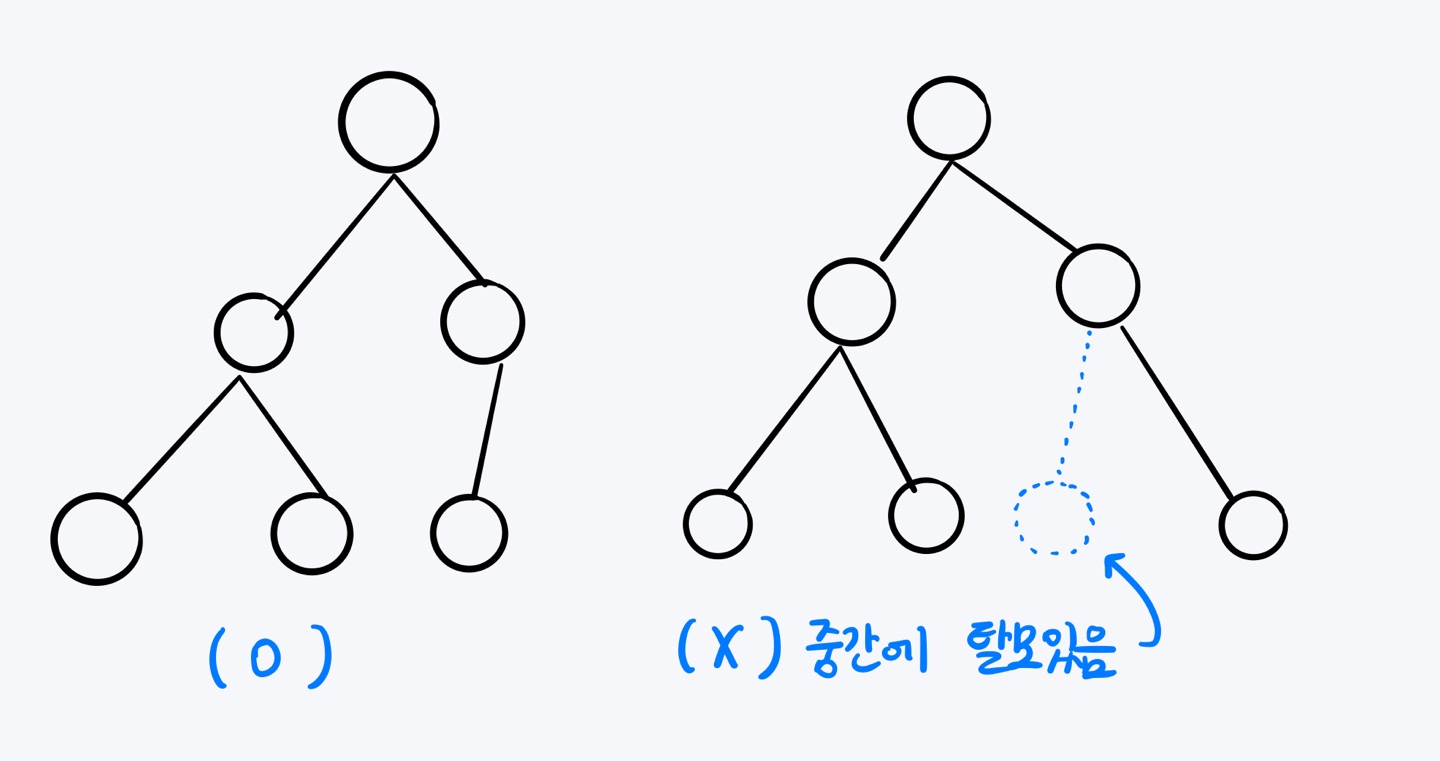
여기서 중요한 것은 아무리 없어도 된다고 한들, 듬성듬성 빠지면 안되고 탈모 무조건 오른쪽부터 가지런히 빠져줘야 한다는 것이다.

당연히, 마지막 레벨의 노드가 꽉 차 있을 수도 있으므로, perfect binary tree는 complete binary tree이다. But 그 반대는 안된다. 왜인지 모르면 다시 읽어라 미래의 나야.

Complete Binary Tree는 배열에 저장하는 것이 효율적

Complete Binary Tree를 입력받을 경우, 탈모 현상 없이 차곡차곡 채워져서 들어오기 때문에 node의 번호를 index로 하여 배열에 저장하는 것이 가장 효율적이다.

Heap

Heap은 complete binary tree를 만족한다.

고로, 앞에는 차곡차곡 탈모 없이 노드들이 있지만 마지막 레벨에서는 노드가 오른쪽부터 일부 없을수도 있다.

Max-heap && Min-heap

Max-heap과 Min-heap의 정의는 한끝 차이이다.

Max Heap	부모 노드는 항상 자식 노드에 들어있는 값 보다 크다 ( 부 >= 자 )
Min Heap	부모 노드는 항상 자식 노드에 들어있는 값 보다 작다 ( 부 <= 자 )

이 차이로 인해서 생기는 트리의 모양은 매우매우 달라진다.

Max Heap

• Max-heap에서 가장 큰 값은 루트에 들어가 있다
• N개가 heap에 들어가 있으면 높이는 $logN$이 된다. (complete binary tree의 특징을 만족하기 때문)

Max Heap 구현

struct MinHeap // heap에 들어오는 범위가 1 ~ 2^31-1 인 경우
{
    vector<unsigned int> heap;
    int count;
    MinHeap(int n) : heap(n + 1, pow(2,31)), count(0) {}

    void insert(unsigned int input)
    {
        heap[++count] = input;

        for (int i = count; i != 1 && heap[i] < heap[i / 2]; i = i / 2)
            swap(heap[i], heap[i / 2]);
    }

    unsigned int pop()
    {
        if (count == 0)
            return 0;

        int front = heap[1];

        swap(heap[1], heap[count]);
        heap[count--] =  pow(2,31); 

        for (int i = 1; i * 2 <= count;)
        {
            if (heap[i] < heap[i * 2] && heap[i] < heap[i * 2 + 1])
            {
                break;
            }
            else if (heap[i * 2] > heap[i * 2 + 1])
            {
                swap(heap[i], heap[i * 2 + 1]);
                i = i * 2 + 1;
            }
            else
            {
                swap(heap[i], heap[i * 2]);
                i = i * 2;
            }
        }
        return front;
    }
};

Min Heap

• Min-heap에서 가장 작은 값은 루트에 들어가 있다.
• N개가 heap에 들어가 있으면 높이는 $logN$이 된다. (complete binary tree의 특징을 만족하기 때문)

Min Heap 구현

struct MaxHeap 
{
    vector<unsigned int> heap;
    int count;
    MaxHeap(int n) : heap(n + 1, 0), count(0) {}

    void insert(unsigned int input)
    {
        heap[++count] = input;

        for (int i = count; i != 1 && heap[i] > heap[i / 2]; i = i / 2)
            swap(heap[i], heap[i / 2]);
    }

    unsigned int pop()
    {
        if (count == 0)
            return 0;

        int front = heap[1];

        swap(heap[1], heap[count]);
        heap[count--] =  0; 

        for (int i = 1; i * 2 <= count;)
        {
            if (heap[i] > heap[i * 2] && heap[i] > heap[i * 2 + 1])
            {
                break;
            }
            else if (heap[i * 2] < heap[i * 2 + 1])
            {
                swap(heap[i], heap[i * 2 + 1]);
                i = i * 2 + 1;
            }
            else
            {
                swap(heap[i], heap[i * 2]);
                i = i * 2;
            }
        }
        return front;
    }
};