[그래프] 그래프 기초

그래프 용어

그래프 G = (V,E)

그래프는 자료 구조의 일종이다. 정점(Node, Vertex)와 간선(Edge)로 이루어져 있으며, 정점의 집합은 보통 V, 간선의 집합은 E로 표시한다.

경로 Path

정점 A에서 B로 가는 경로는 다양하게 말할 수 있다.

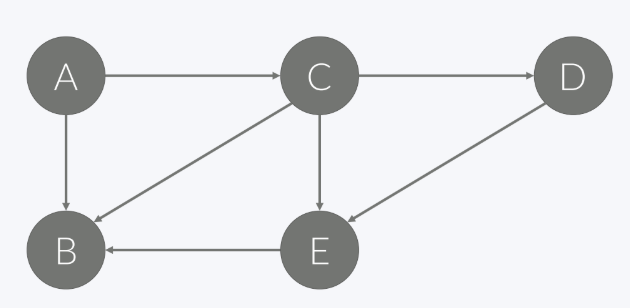
• A -> B
• A -> C -> B
• A -> C -> E -> B
• A -> C -> D -> E -> B

따라서, 어떤 정점에서 다른 정점으로 가는 경로는 여러가지일 수 있다.

사이클 Cycle

한 정점에서 다시 그 정점으로 돌아가는 모든 경로를 말한다.

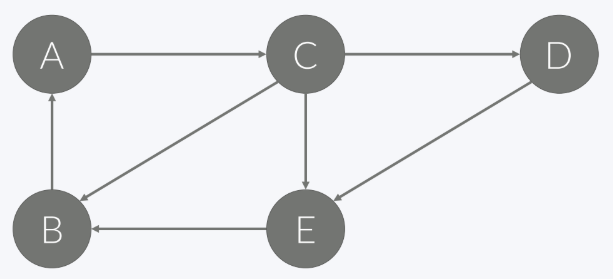
정점 A에서 정점 A로의 사이클은 다음과 같다

• A -> C -> B -> A
• A -> C -> E -> B -> A
• A -> C -> D -> E -> B -> A

따라서, 어떤 정점에서 그 정점으로의 사이클은 여러가지일 수 있다.

단순 경로(simple path)와 단순 사이클(simple cycle)

'단순'이라는 말의 의미는 경로나 사이클에서 같은 정점을 두 번 이상 방문하지 않음을 의미한다.

보통 알고리즘 문제에서 볼 수 있는 대부분의 그래프에서의 경로는 같은 정점을 두 번 이상 방문하지 못하는 경우이므로 우리가 일반적으로 사용하는 경로와 사이클은 따로 언급이 없다면 단순 경로와 단순 사이클이다.

방향 그래프 directed graph

간선에 방향이 표시되어있는 그래프를 의미한다.

무방향 그래프 undirected graph

간선에 방향이 표시되어있지 않은 그래프를 의미한다.

만약 정점 A와 B 사이에 간선이 존재할 경우, 이는 A -> B 와 B -> A 가 모두 가능함을 의미한다. 이에 따라 양방향 그래프(bidirectied graph) 라고도 불린다.

알고리즘 문제를 풀 때에는 양쪽 간선(A -> B, B -> A)을 모두 저장하여 마치 방향 그래프를 저장하듯이 문제를 푼다.

간선 여러개 multiple edge

두 정점 사이에 간선이 여러 개일 수도 있다. 이 경우, 같은 정점에서 출발하여 같은 정점에 도착하더라도 여러 개의 간선은 서로 다른 간선이다.

루프 loop

간선의 양 끝점이 같은 간선을 루프(loop)라고 한다.

가중치 weight

간선에 가중치가 표시되어 있는 경우도 있다. 이 경우 가중치는 정점을 이동하는 거리, 이동하는데 필요한 시간, 이동하는데 필요한 비용 등으로 해석할 수 있다.

가중치가 없는 경우는 가중치를 1로 생각해서 문제를 풀면 된다.

차수 degree

한 정점에 연결되어 있는 간선의 개수를 의미한다.

방향 그래프일 경우에는 차수가 indegree와 outdegree 두 가지로 나뉘게 된다.

방향그래프에서 차수를 세어 줄 때에는 indegree와 outdegree를 따로 세어 주어야 한다.

[ 출처 ] 백준 온라인 강의