알고리즘 divide and conquer - merge sort

Divide and conquer란?

큰 문제를 작은 문제로 나눠 해결한 다음 다시 하나로 합치는 것을 말합니다.
이 divide and conquer 중 정렬 알고리즘인 merger sort를 알아보겠습니다.

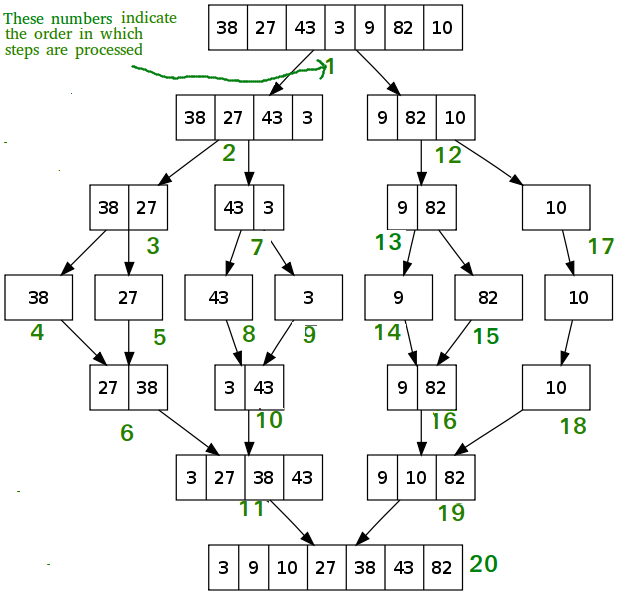
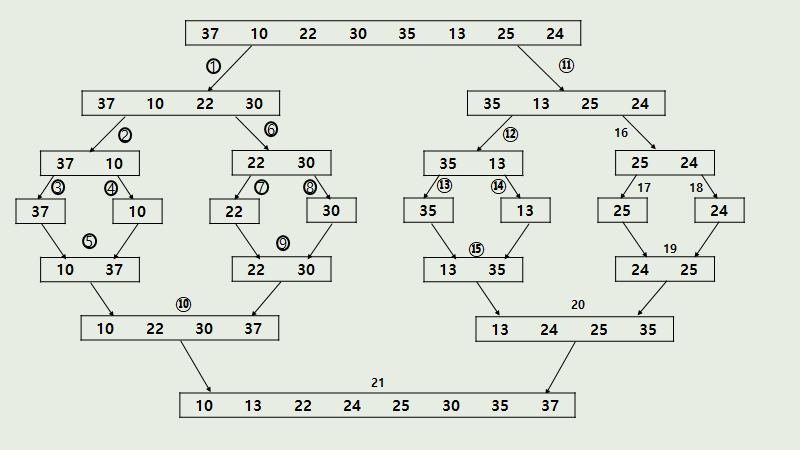
알고리즘 설명

divde

1번의 원본 데이터에서 각각 2번, 12번 데이터로 divide 합니다. 이 때 divide의 기준은 원본 데이터의 상위 데이터(2번과 12번의 부모 데이터)의 중간값입니다.
1번 데이터에서 left = 0 right = 7이니 중간인 mid = 3이 됩니다.
그럼 2번은 0~3, 12번은 4~7이 되겠죠? 이렇게 절반으로 divide 하면 어느 순간 데이터의 크기가 1이 되는 순간이 옵니다.

conquer

이제 divide를 멈추고 각 데이터들 간의 비교를 통해 정렬을 합니다.
코드로 설명하겠습니다.

코드 예시

// mergeSort 구현
    public static void mergeSort(Point[] points, int left, int right) {
    // 데이터가 1개면 멈춤
        if (left < right) {
            int mid = (left + right) / 2;

            // 왼쪽 및 오른쪽 부분 배열을 재귀적으로 정렬
            mergeSort(points, left, mid);
            mergeSort(points, mid + 1, right);

            // 합치기
            merge(points, left, mid, right);
        }
    }

    // merge 함수: 두 부분 배열을 합치며 정렬
    public static void merge(Point[] points, int left, int mid, int right) {
    //해당 구간의 데이터들을 복사
        int n1 = mid - left + 1;
        int n2 = right - mid;
	
        Point[] L = new Point[n1];
        Point[] R = new Point[n2];

        for (int i = 0; i < n1; ++i) L[i] = points[left + i];
        for (int j = 0; j < n2; ++j) R[j] = points[mid + 1 + j];

        int i = 0, j = 0;

        int k = left;
        //크기 비교 후 원본 데이터를 변경
        while (i < n1 && j < n2) {
            if (L[i].compareTo(R[j]) <= 0) {
                points[k] = L[i];
                i++;
            } else {
                points[k] = R[j];
                j++;
            }
            k++;
        }

        // 남은 요소들을 복사
        // left와 right의 크기 비교 중 한 쪽의 데이터만 남은 경우 
        // 남은 데이터를 차례대로 저장
        while (i < n1) {
            points[k] = L[i];
            i++;
            k++;
        }

        while (j < n2) {
            points[k] = R[j];
            j++;
            k++;
        }
    }

이게 기본적인 merge sort의 구조입니다. 특히 java를 사용하시는 분들은 Compare 인터페이스 (Compareable, Comparator)를 사용하실텐데 이 인터페이스의 compare 로직이 바로 이 merge sort라고 합니다.

각 정렬 예시

 static void mergeSort(Point [] points, int left, int right){
        if(left< right){
            int mid = (left+right)/2;
            mergeSort(points,left, mid);
            mergeSort(points,mid+1,right);

            merge(points,left,mid,right);

        }

    }
    static void merge(Point [] points, int left ,int mid,int right){
        int aSize = mid -left +1;
        int bSize = right-mid;
        Point [] a = new Point[aSize];
        Point [] b = new Point[bSize];

        for(int i = 0 ; i<aSize; i++){
            a[i] = points[left + i];
        }
        for(int i =0;i<bSize;i++){
            b[i] = points[mid +1 +i];
        }
        int i=0 , j=0;
        int index = left;
        while(i<aSize && j <bSize){
            double angle1 = calAngle(startPoint, a[i]);
            double angle2 = calAngle(startPoint, b[j]);
            if (angle1 < angle2) {
                points[index] = a[i];
                i ++;
            }
            else if(angle1>angle2){
                points[index] = b[j];
                j++;
            }else{
                int result = dist(a[i],b[j]);
                if(result == -1){
                    points[index] = a[i];
                    i ++;
                }else{
                    points[index] = b[j];
                    j++;
                }

            }
            index++;
        }
        while(i<aSize){
            points[index] = a[i];
            i++;
            index ++;
        }
        while(j<bSize){
            points[index] = b[j];
            j++;
            index++;
        }
    }
    static double calAngle(Point a, Point b) {
        return Math.atan2((b.y - a.y), (b.x - a.x));
    }
    static int dist(Point a, Point b){
        double dist1 = (startPoint.x - a.x) * (startPoint.x - a.x) + (startPoint.y - a.y) * (startPoint.y - a.y);
        double dist2 = (startPoint.x - b.x) * (startPoint.x - b.x) + (startPoint.y - b.y) * (startPoint.y - b.y);
        if (dist1 < dist2) return -1;
        else return 1;
    }

기본적인 정렬 알고리즘인 선택 알고리즘은 시간 복잡도가 O(N2)이기 때문에 굉장히 간단하지만 비효율적인데요. 병합 알고리즘은 O(NlogN)이기 때문에 데이터가 많은 경우에는 조금 복잡하더라고 병합 알고리즘을 사용하시면 코딩테스트에서 성능적으로 이점을 얻을 수 있습니다.