Lexical Anaysis 는 Compilation의 첫 번째 단계이다. given sequence of string - code - 에서 token을 분리해내는 단계이다.
Role of a Scanner
Scanner의 역할은 Stream of characters를 words로 바꾸는 것이고, 이러한 word들을 Token이라고 부른다. Token은 syntax의 unit이다. -Introduction의 예시 참고!- Token은 보통 <type, value>로 표기한다. (Tuple)
여기서 Lexeme이라는 개념이 나오는데, word를 구성하는 character들이다. Lexeme이라는 개념을 이해하기 어려웠는데, Pattern과 비교하여 예시를 보면 비교적 쉽게 이해할 수 있다.
Pattern은 특정한 Token type을 정의하는 규칙이다. 이 또한 예시로 함께 살펴보자.
Token type : ID (Identifier)
Pattern : A string of letters, digits, and underscores, beginning with a letter or underscore
Set of Lexemes : {var, _var, ptr_1, foo, foo123}
Token type은 어떠한 종류의 token인지를 나타낸다. 예시처럼 identifier가 될 수도 있고 INTLITERAL -Integer 값- 이나 if while과 같은 제어문, +나 * 같은 arithmetic 기호가 될 수도 있다. Pattern은 이러한 token type의 규칙의 정의이다.
Identifier의 경우 대부분의 high-level 언어에서 문자나 _로 시작하는 것을 규칙으로 하고 그 뒤로 문자와 숫자, _의 어떠한 조합도 가능하다. INTLITERAL의 경우 pattern은 decimal digits의 조합이 될 것이다.
Set of lexemes는 이러한 pattern으로 정의된 token type의 possible sets다. 즉 인 는 Pattern을 만족하는 string이라고 볼 수 있다. Pattern 에 의해 정의되는 set of lexemes를 라고 정의한다.
기본적인 에 대한 연산들
Regular Expression
이제 Pattern이 무엇인지 알았으니 그 중요성 또한 알 수 있다. Token type을 정의하고 set of lexemes를 규제하는 것이 pattern이기에 이러한 pattern에 대한 formal한 notation을 정의할 필요성을 느낄 수 있다.
Scanner를 만들기 위해서는 Pattern에 대한 정보인 specification 을 명확히 해야 하는데, natural language로 이를 표현하면 서로 다른 기준의 specification들이 형성된다. 이는 수학적(일관적)이지 않다! 이러한 통용되는 specification을 만든 것을 Regular Expression(RE) 이라고 부른다. Lexeme은 finite set인 에 속하는 character들로 만들어지고, 이러한 finite set 를 alphabet 이라고 부른다.
의 character를 쓸 때에는 구분하기 위해서 을 사용한다. alphabet 에 대해서 inductive definition은 아래와 같다.
R1 : is a RE denoting the set {}
R2 : If is in , then is a RE denoting the set {}
If x and y are REs denoting and then
R3: is a RE denoting -> "alternation"
R4: is a RE denoting -> "concatenation"
R5: is a RE denoting -> "repetation" or "closure"
되게 당연해 보이는 얘기들이다. 그냥 한 번 보고 넘어가면 될 듯 하다. 다만 사칙연산처럼 우선순위(Precedence)를 가지는데, closure > concatenation > alternation 순이다. 다만, parenthesis가 있다면 parenthesis가 먼저이다.
Shorthand Notation도 존재한다. 는 많이 쓸듯?
Automata theory와 Theory of algorithm의 결과들로 recognizer를 만들 수 있다. 이때 RE로 표현하여 사용한다.
"We study REs and associated theory to automate scanner construction"
Automata - DFA
Automata theory를 어떻게 활용할 것인지에 대해 논의할 차례이다. RE는 set of lexemes를 묘사하는 pattern을 수식적으로 나타내는 방법론이였다. 그리고 RE에는 '순서'가 있다. 와 같은 RE에서는 이 나온 이후에 다른 경우의 수가 고려될 수 있다. 이러한 순서를 가지고 있는 RE는 Finite Automata로 나타낼 수 있다.
예를 들어 Register를 표현하는 RE는 와 같은 shorthand notation을 포함한 RE로 나타낼 수 있고 이를 Finite Automata로 나타내면 아래 그림과 같다. - 아래와 같은 형태를 Finite Automata라고 한다. -
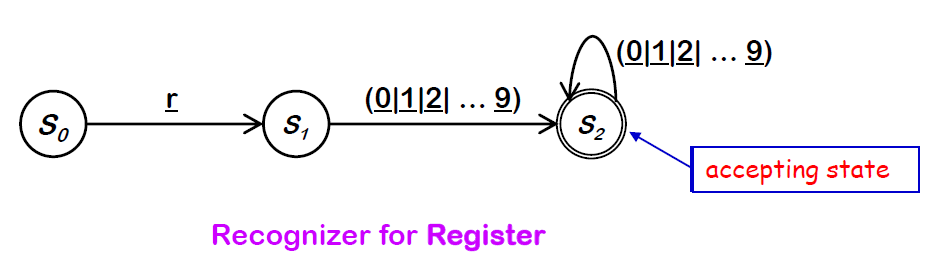
여기서 Accepting state에 최종적으로 도달해야지만 Register로 받아들여진다. 만약 다른 state로 전이하는 과정에서 경우의 수에 해당하지 않는 가 input으로 들어오면 라는 error state로 진입한다.
Finite Automata를 구성하는 요소 5개는 이고 이는 각각 아래와 같은 의미이다.
- is an alphabet
- is a finite set of states
- is a state transition function
- is a set of final or accepting states
- is the start state
여기서 는 모든 에 대하여 각각의 , 조합에서 다음 state가 어디인지를 나타낸 table이라고 생각할 수 있다.
이렇게 특정 를 판단하는 방법으로 FA를 사용할 수 있다. 그리고 그러한 FA중 diterministic한 FA를 DFA라고 부른다.
DFA accepts input string leaves it in an accepting state
그렇다면 RE로 나타낸 pattern들은 모두 FA로 나타냈을 때 deterministic할까?
Automata - NFA
와 같은 경우를 생각해보자. 이러한 pattern은 아래와 같은 FA로 나타낼 수 있다.
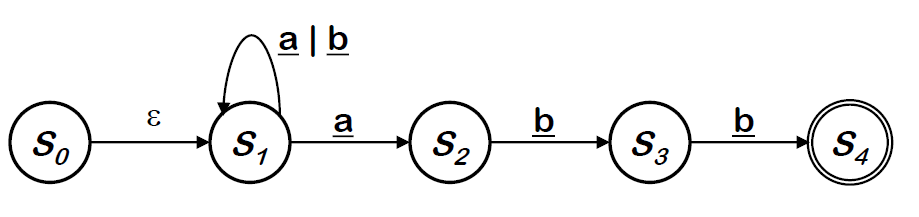
에서 input으로 가 들어왔을 때 우리는 으로 갈 수도 있고, 로 갈 수도 있다. 여기서 어떤 선택을 해야 하는가? 단순한 '예측'으로 시도해볼 수 밖에 없다. 이러한 FA를 Non-deterministic Finite Automata라고 한다.
NFA accepts input string
DFA는 NFA의 special case라고 볼 수 있다. DFA는 transition이 없으며 transition function은 single-valued이다.
Definition of DFA & NFA
A FA is a DFA if
- No state has an -transition, i.e., there is no transition on input
- For each state s and input symbol , there is at most one edge labeled leaving state s.
A FA is an NFA
- if it contatins -transition or
- if it has several possible transitions from a state s on a given input symbol .
To convert a specification to code:
1. Write down the RE for the input language
2. Build a big NFA
3. Build the DFA that simulates the NFA
4. Minimize the number of states in the DFA
5. Generate the scanner codeDFA와 NFA는 Scanner Construction을 위해 알아야 했다. 이제 NFA를 simulation할 수 있는 DFA를 만드는 방법과 그러한 DFA를 minimize하는 방법을 소개한다. 이러한 과정을 이해하면 Scanner Generation을 수행할 수 있다! 아마도..
Automating Scanner Construction
RE -> NFA (Thompson's construction)
RE를 인수분해 한다고 생각하고 각각의 NFA를 만든다. 그 후 만들어진 NFA -어떤 RE를 표현하는-를 다른 NFA와 순서에 맞게 연결한다. 이때 NFA와 NFA를 -transition으로 연결한다. 이때 symbol 가 RE에서 여러번 등장하더라도 각각에 맞는 NFA를 만들어야 하는 점을 주의해야 한다.
예시 몇개 보면 이해할 수 있는 정도이다. 아래 그림을 참고하자.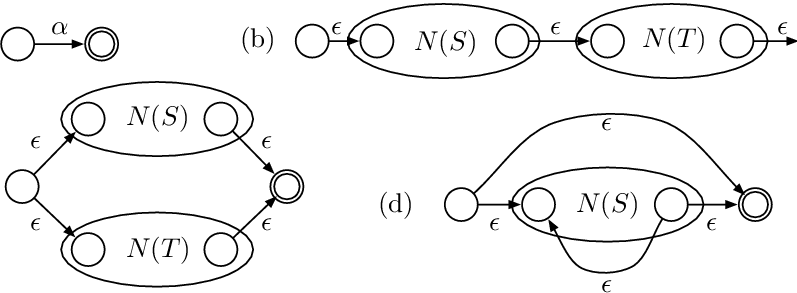
Reference : New Algorithms for Regular Expression Matching - Scientific Figure on ResearchGate. Available from: https://www.researchgate.net/figure/Thompsons-NFA-construction-The-regular-expression-for-a-character-a-S-corresponds-to_fig1_1959575 [accessed 22 Oct, 2022]
NFA -> DFA (subset construction)
NFA의 정의에서 알 수 있듯이 FA가 -transition을 가지고 있거나 한 쌍에서 두가지 이상의 transition이 가능하다면 NFA이다. NFA를 DFA로 바꾸기 위해서는 이 두가지를 없애야 한다. 의 예시에서 의 transition이 두가지 방향으로 가능했다. subset construction에서는 이 두가지 방향으로의 transition을 'parallel'하게 진행한다. 그리고 이러한 parallel한 transition을 n가지 State를 합친 virtual state로 표현한다.
- 어떤 State 에서 같은 에 대해 n개의 transition 이 가능한 경우 그 가능한 State들을 모두 합친 virtual state를 만든다.
- virtual state 혹은 state에서 모든 에 대해 어떤 transition이 가능한지 보고 이를 반복한다.
- 반복하면서 -transition이 있는 경우 합치는게 가능하다면 합쳐준다.
여기서 가장 어려웠던 부분이 만약 과 를 합친 virtual state가 존재하고, 그러한 virtual state에서 어떤 input 에 대해 는 가 아닌 State로 transition이 가능하지만 가 로 transition하는 경우에는 어떻게 하지? 였다.
해답은 그렇게 어렵지 않았는데, 그냥 virtual state로 transition하게한 input이 를 통과하는 path를 가진다고 생각하면 되는 일이었다. 이부분 말고는 어려운 부분은 없는 것 같다. 공부한 강의안에는 복잡한 알고리즘이 적혀 있었기에 정확한 알고리즘을 공부하고 싶은 사람은 참고하자. subset construction도 예제 문제 몇개 풀어보면 금방 감을 잡을 수 있을 것 같다.
DFA -> minimal DFA (Hopcroft's algorithm)
NFA에서 simulation을 위한 DFA를 만들었으니 그 DFA를 minimal하게 만들 차례이다. minimal하게 만들어야 하는 이유는 여러가지가 있겠지만 computation cost를 줄이기 위함이 큰 이유중 하나가 아닐까라고 추측했다.
먼저 State의 distinguishable에 관해 논해야 한다. 그 후에 distinguishable하지 않은 state들을 합치는 과정을 통해 DFA를 minimize한다.
Distinguishable에 대한 확인은 쉽다. Partition과 같은 새로운 개념을 활용하여 배웠지만 그 전에 이해를 돕기 위해 나름대로 이해한 내용을 전달하고자 한다. 어떤 와 가 에 대해서 같은 transition을 가진다면 이를 distinguishable하지 않다고 한다. 이렇게 distinguishable하지 않은 State들을 합치는 과정이 mimimazation이라고 볼 수 있다.
아래는 조금 더 수식적이고 정밀한 정리이다.
Partition
Partition은 at least one State가 포함된 집합이다. 같은 Partition에 존재하는 State는 not distinguishable하다. 어떤 State든 하나의 Partition에만 속한다.
처음 Partition은 2개의 집합으로 나뉜다. Final State 와 이다. 이 둘은 으로 distinguishable하다.
와 에 대하여 distinguishable한지 판단한다. 이를 반복한다.
알고리즘을 보면 머리가 복잡하지만 간단한 예시를 통해 쉽게 접근이 가능했다. 에 대한 예시이다.

Cf> Limitations of Regular Languages
과 같은 것을 REs로 표현할 수 없다.
Context free grammer
Programming Languages exhibit self embedding -> Will handle it in Syntax Analysis


