[알고리즘] 거품 정렬 Bubble Sort

    서로 인접한 두 원소의 대소를 비교하고, 조건에 맞지 않다면 자리를 교환하며 정렬하는 방법이다.

• 안정 정렬(stable sort): 정렬되지 않은 상태에서 같은 키 값을 가진 원소의 순서가 정렬 후에도 유지된다.
• 제자리 정렬(In-place): 주어진 공간에 비해 추가적인 공간을 사용하지 않거나, 주어진 원소들의 개수에 비해서 무시할 만한 저장 공간만을 더 사용하는 정렬
     

  1회전: 첫번째 원소 vs 두번째 원소, 두번째 원소 vs 세번째 원소, ..., (n-1)번째 원소 vs n번째 원소를 비교하면서 조건에 맞지 않는다면 자리를 교환한다.
  => 가장 큰 원소가 제일 뒤에 위치하게 된다.(오름차순) 맨 끝에 있는 원소 정렬에서 제외
  
  2회전: 첫번째 원소 vs 두번째 원소, 두번째 원소 vs 세번째 원소, ..., (n-2)번째 원소 vs (n-1)번째 원소 비교하며 정렬
  => 끝에서 두번째 원소까지 정렬에서 제외
  
  .
  .
  .
  
  이 과정을 반복한다.

• 코드

#include <iostream>

using namespace std;

int main() {
    int data[] = {7, 4, 5, 1, 3};
    
    for(int i=0; i<5; i++){
        for(int j=0; j<5-(i+1); j++){
            if(data[j+1]<data[j]){
                int temp = data[j+1];
                data[j+1] = data[j];
                data[j] = temp;
            }
        }
    }

    return 0;
}

• 정렬 알고리즘 별 시간 / 공간 복잡도 표
  

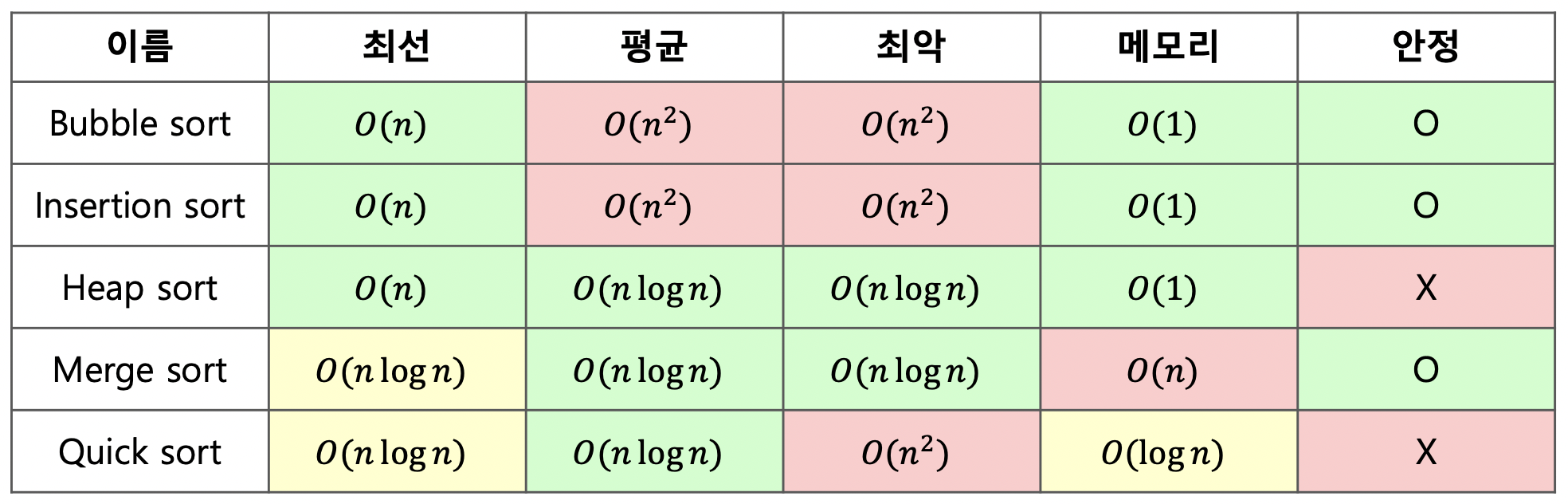
• 시간복잡도: O(n^2)

  시간복잡도
  최선	Ω(n)
  평균	Θ(n^2)
  최악	O(n^2)

  (n-1) + (n-2) + (n-3) + .... + 2 + 1 = n(n-1)/2
  한 번의 순회가 끝나면 비교할 원소가 하나씩 줄어든다. 전체 개수가 n개일 때 n-1번 순회하면 정렬이 끝난다. 최선의 경우(이미 정렬된 경우) 전체 자료를 한 번 순회하기만 하면 된다.

• 공간복잡도: O(1)
  주어진 배열 안에서 교환(swap)