유클리드 호제법
호제법이란 말은 두 수가 서로(互) 상대방 수를 나누어(除)서 결국 원하는 수를 얻는 알고리즘
-
최대공약수: 2개의 자연수 a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a>b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다. 이 성질에 따라, b를 r로 나눈 나머지 r'를 구하고, 다시 r을 r'로 나눈 나머지를 구하는 과정을 반복하여 나머지가 0이 되었을 때 나누는 수가 a와 b의 최대공약수이다
=> gcb(a, b) = gcb(b, r) -
최소공배수: a * b / 두 수의 최대공약수
💡 관련문제: 프로그래머스 Level2 N개의 최소공배수
두 수의 최소공배수(Least Common Multiple)란 입력된 두 수의 배수 중 공통이 되는 가장 작은 숫자를 의미합니다. 예를 들어 2와 7의 최소공배수는 14가 됩니다. 정의를 확장해서, n개의 수의 최소공배수는 n 개의 수들의 배수 중 공통이 되는 가장 작은 숫자가 됩니다. n개의 숫자를 담은 배열 arr이 입력되었을 때 이 수들의 최소공배수를 반환하는 함수, solution을 완성해 주세요.
#include <string>
#include <vector>
#include <algorithm>
using namespace std;
int gcd(int x, int y) { return x % y == 0 ? y : gcd(y, x % y); }
int lcm(int x, int y) { return x * y / gcd(x, y); }
int solution(vector<int> arr) {
int answer = arr[0];
for (int i = 1; i < arr.size(); i++)
answer = lcm(answer, arr[i]);
return answer;
}베주 항등식
정수 a, b의 최대공약수를 gcd(a,b)로 나타낼 때, 확장 유클리드 호제법을 이용하여 ax+by = gcd(x,y)의 해가 되는 x, y를 찾아낼 수 있다.(보통 x, y 중 하나는 음수)
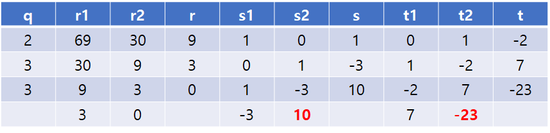
확장 유클리드 호제법
ax+by=c 형태의 방정식이 주어질 때 이 방정식을 만족시키는 정수 x, y를 각각 s, t라고 정의하고 우변의 상수값에 유클리드 호제법을 사용하여 반복적으로 구하는 값들을 r이라고 하면 아래 방정식을 만족시키는 정수 해 s와 t가 반드시 존재 ((1,0), (0,1))
- ax+by = a
- ax+by = b
여기서부터 아래 단계를 반복적으로 적용하면서 rㄱ밧을 줄여나가면 최종적으로 우변의 값을 만들 수 있는 r값을 찾을 수 있고, 이 때 s와 t값을 통해 해를 구할 수 있다.
① r = r''-qr'식을 통해 q와 r을 계산한다.
② s = s''-qs', t = t''-qt'식을 통해 s와 t를 계산한다.
69x + 30y = 12