[알고리즘] 퀵 정렬 Quick Sort

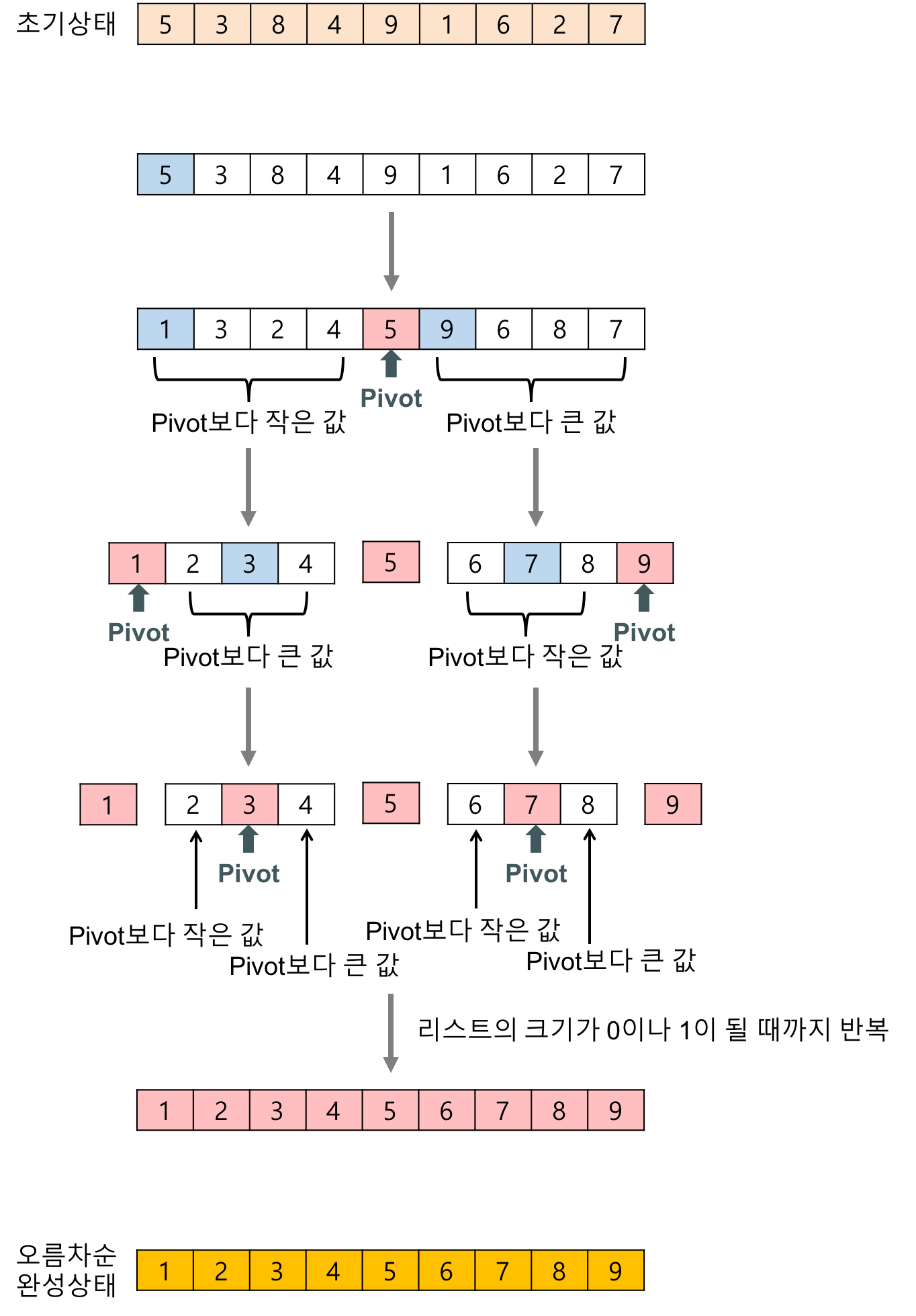
    하나의 리스트를 피벗(pivot)을 기준으로 두 개의 비균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법

• 분할 정복(Divide and Conquer) 전략: 문제를 작은 2개의 문제로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략으로, 대개 순환 호출을 이용

  • 분할(Divide): 입력 배열을 피벗을 기준으로 비균등하게 2개의 부분 배열(피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)로 분할한다.
  • 정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용한다.
  • 결합(Combine): 정렬된 부분 배열들을 하나의 배열에 합병한다.순환 호출이 한번 진행될 때마다 최소한 하나의 원소(pivot)는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.

• 불안정 정렬(unstable)

• 피벗 선택 방식에 따라 속도가 달라짐
  

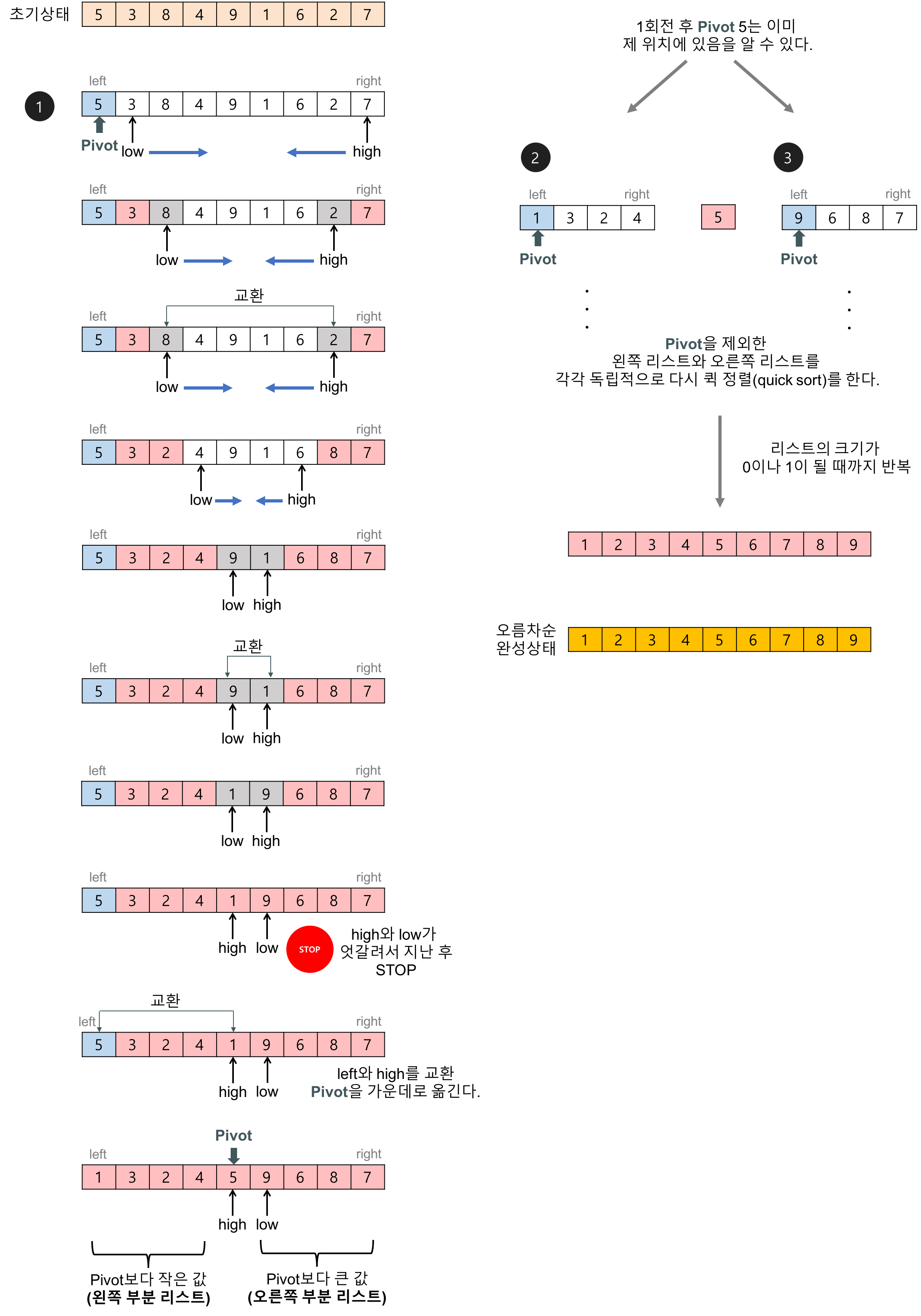
  1. 피벗 선택
  2. 오른쪽(high=>i)에서 왼쪽으로 가면서 피벗보다 작은 수 찾음
     왼쪽(low=>j)에서 오른쪽으로 가면서 피벗보다 큰 수 찾음
  3. 각 인덱스 i, j 대한 요소를 교환
  4. 2,3번 과정 반복
  5. 더이상 2,3번 진행이 불가능하면, 현재 피벗과 교환
     교환된 피벗 기준으로 왼쪽엔 피벗보다 작은 값, 오른쪽엔 큰 값들만 존재함
  6. 이 과정을 반복함

• 코드

#include <iostream>
using namespace std;

int n,cnt, quick[10000001];

void quickSort(int i, int j)
{
	if(i>=j) return;
	int pivot = quick[(i+j)/2];//가운데를 pivot으로
	int left = i;
	int right = j;
	
	while(left<=right)
	{
		while(quick[left]<pivot) left++;
		while(quick[right]>pivot) right--;
		if(left<=right)
		{
			swap(quick[left],quick[right]);
			left++; right--;
		}
	}
	quickSort(i,right);
	quickSort(left,j);
}

int main() 
{
	scanf("%d",&n);
	for(int i = 0; i < n; i++)
		scanf("%d",&quick[i]);

	quickSort(0,n-1);

	for(int j = 0; j < n; j++) // 출력
		printf("%d\n",quick[j]);
}

• 시간복잡도

  시간복잡도
  최선	Ω(nlog(n))
  평균	Θ(nlog(n))
  최악	O(n^2)

  -최선의 경우:
  
     =>Ω(n log(n))
  
  -최악의 경우: pivot이 최대나 최소인 경우(이미 정렬된 배열에서 첫번째 값을 pivot으로)
  
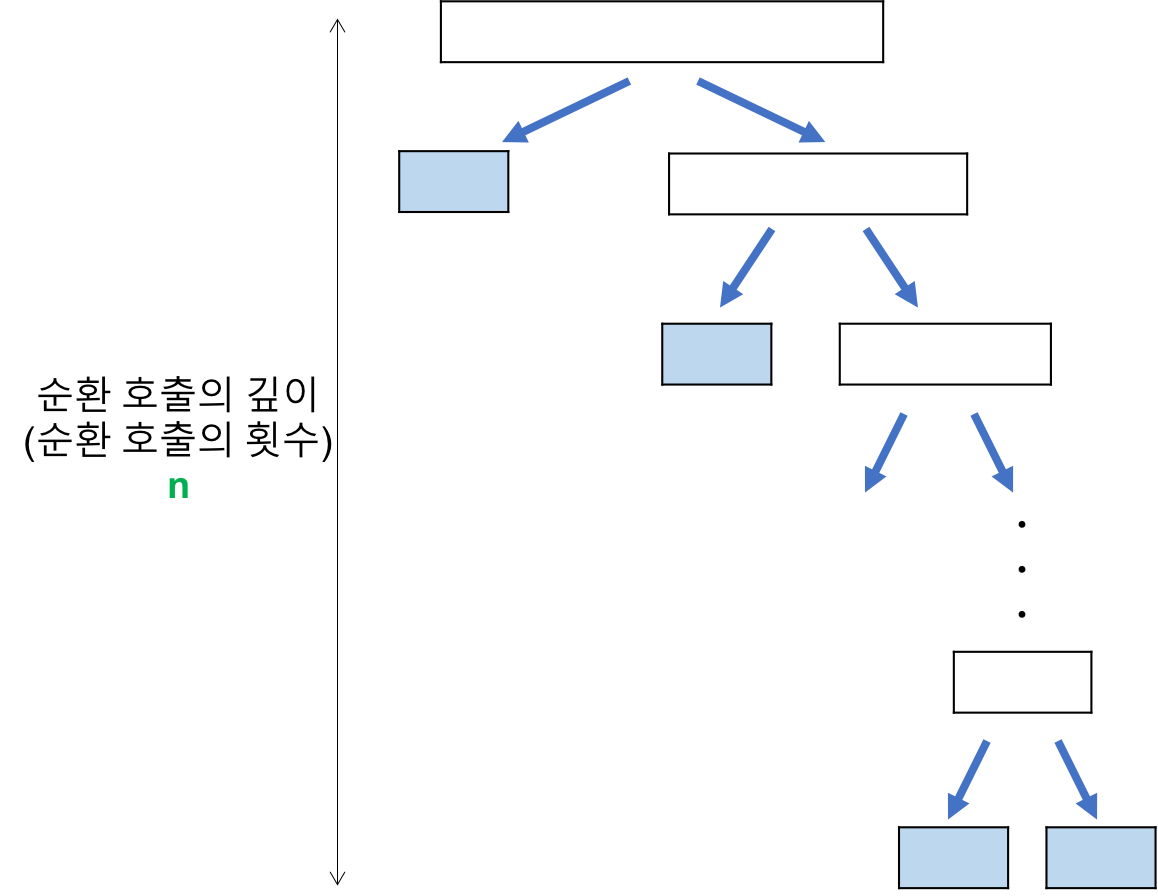
     =>O(n^2)

참고링크