💡 그래프 Graph란?
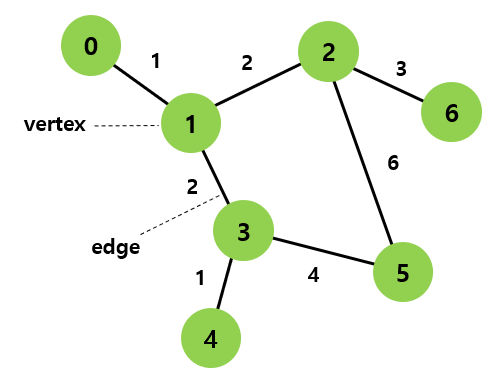노드(node)와 그 노드를 연결하는 간선(edge)을 하나로 모아 놓은 비선형 자료 구조
- 트리 또한 그래프의 일종으로, 사이클이 없는 그래프를 트리라고 함
그래프 G = (V, E)
V(G) = 정점(Vertices)
E(G) = 간선(Edges)그래프 용어
- 무항 간선(Undirected Edge): 정점을 연결하는 간선에 방향이 존재하지 않음
- 유항 간선(Directed Edge): 정점을 연결하는 간선에 방향이 존재. 임의의 간선 (vi, vj)에 대해 (vi, vj)≠(vj, vi)
- 인접(Adjacent): 정점 vi, vj에 대해 간선 e = (vi, vj)가 존재하면 정점 vi와 vj는 인접
- 부속(Incidnet): 정점 vi, vj에 대해 간선 e = (vi, vj)가 존재하면 간선 e는 정점 정점 vi와 vj에 부속
- 차수(Degree): 정점에 부속된 간선의 수
- in-degree: 방향 그래프에서 정점에 들어오는 간선의 수
- out-degree: 방향 그래프에서 정점에서 나가는 간선의 수
- 경로(Path): 임의 정점에서 다른 정점으로 이르는 길
- 경로 길이(Path Length): 경로상 있는 간선의 수
- 단순 경로(Simple Path): 한 경로의 모든 간선이 다른 때의 경로
- 회로(Cycle): 동일 정점에서 시작과 끝이 이어지는 경로
- 연결됨(Connected): 정점 vi에서 정점 vj로의 경로가 존재하면, 정점 vi와 정점 vj는 연결되어 있음
💡 단절점 Articulation Points/Cut Vertices
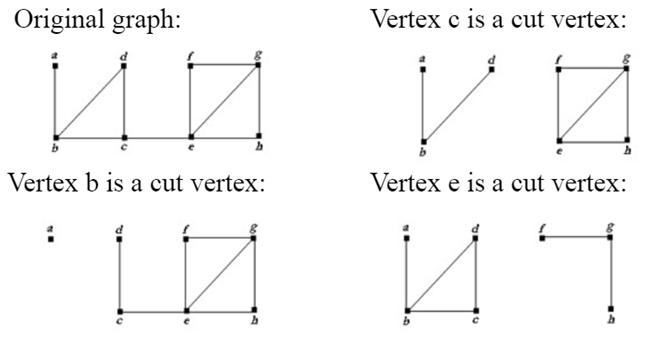무향 연결 그래프 G에서 하나의 정점과 연결된 간선들을 제거했을 때 두 개의 연결 그래프로 나뉘어 진다면 해당 정점은 단절점
- 무향 연결 그래프 G에서 어떤 정점 A에 연결된 정점들에 대해서 우회경로(정점 A를 거치지 않는 경로)가 없는 경우가 존재한다면 A는 단절점
💡 그래프 Graphd의 종류
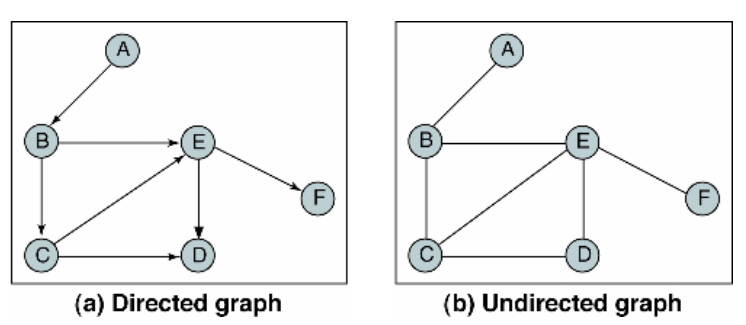
무향 그래프(Undirected Graph)
무향 간선으로 이루어진 그래프
유향 그래프(Directed Graph)
유향 간선으로 이루어진 그래프
가중치 그래프(Weighted Graph)
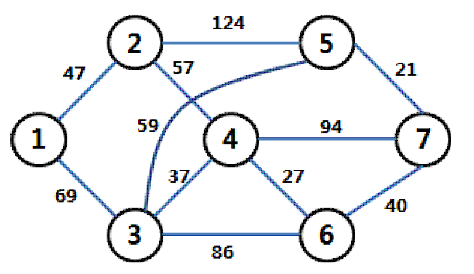
가중치를 갖는 간선으로 이루어진 그래프
정규 그래프(Regular Graph)
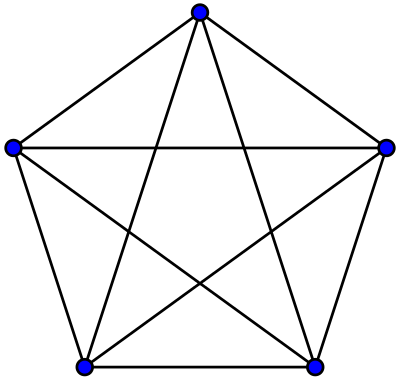
모든 정점이 동일한 차수를 가지는 그래프
완전 그래프(Complete Graph)
임의의 두 정점 vi와 정점 vj에 대해서 vi, vj를 잇는 간선 Edge(vi, vj)이 존재하는 그래프로, 완전 그래프는 정규 그래프. 각 정점에서 다른 모든 정점을 연결하기 때문에 최대 간선 수를 가짐
- N개의 정점을 가지는 무향 그래프의 간선 개수: n(n-1)/2개
- N개의 정점을 가지는 유향 그래프의 간선 개수: n(n-1)개
연결 그래프(Connected Graph)
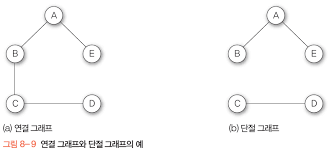
임의의 두 정점 vi와 정점 vj에 대해서 경로 Path(vi, vj)가 존재하는 그래프
부분 그래프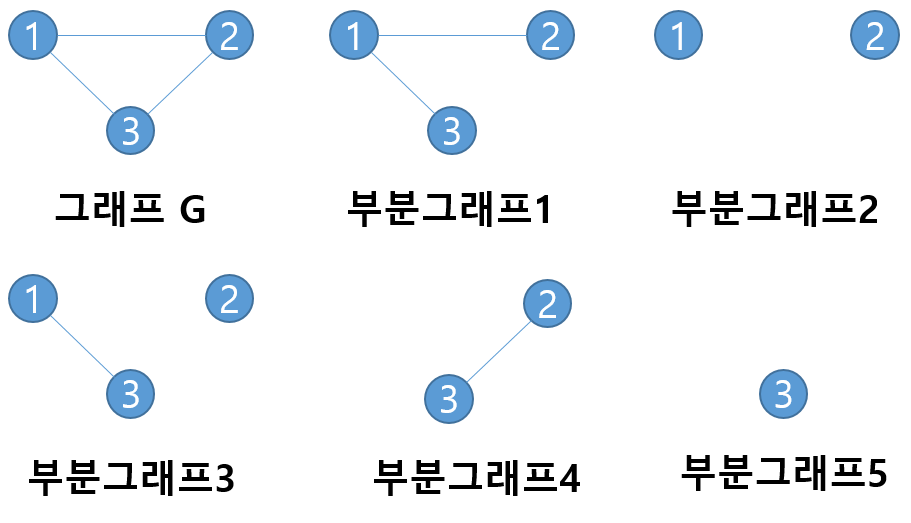
- 어떤 그래프의 정점집합의 부분집합과 그에 속한 간선들로 이루어진 그래프
- 어떤 그래프의 간선집합의 부분집합과 그에 속한 정점들로 이루어진 그래프
트리 그래프
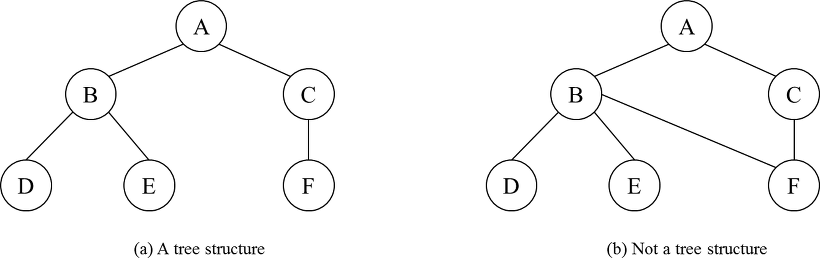
순환을 갖지 않는 연결 그래프로, 임의의 두 정점에 대해서 경로가 정확히 1개 존재
💡 그래프 Graph의 표현
간선 리스트(Edge List)
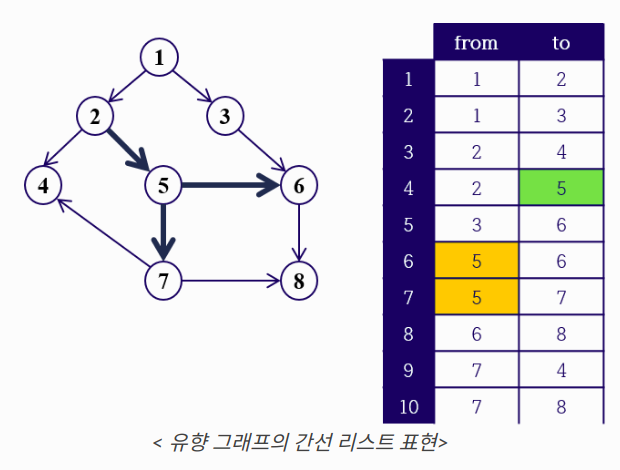
- 정점의 개수가 V개, 간선의 개수가 E개인 그래프에 대해서 E2(or E3) 이차원 배열 A에 간선 정보 저장
- 어떤 두 정점 vi, vj를 연결하는 간선 ek=(vi, vj)에 대해서 A[k][0]= vi, A[k][1]=vj
- 가중치 그래프의 경우 배열의 3번째 열에 간선의 가중치 저장
인접 행렬(Adjacency Matrix)
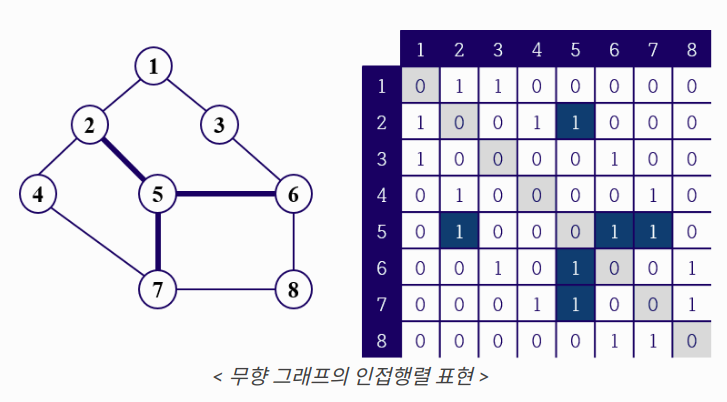
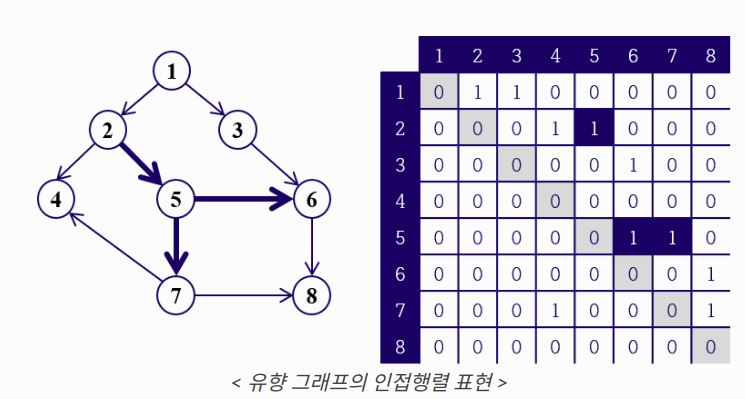
- 정점의 개수가 V개, 간선의 개수가 E개인 그래프에 대해서 V*V 이차원 배열 A에 그래프 정보 저장
- 어떤 정점 vi, vj를 연결하는 간선 ek=(vi, vj)가
- 존재하면 => A[i][j] = 1(or 가중치)
- 존재하지 않으면 => A[i][j] = 0
- 어떤 정점 vi, vj가
- 인접하면 => A[i][j] = 1(or 가중치)
- 인접하지 않으면 => A[i][j] = 0
인접 리스트(Adjacent List)
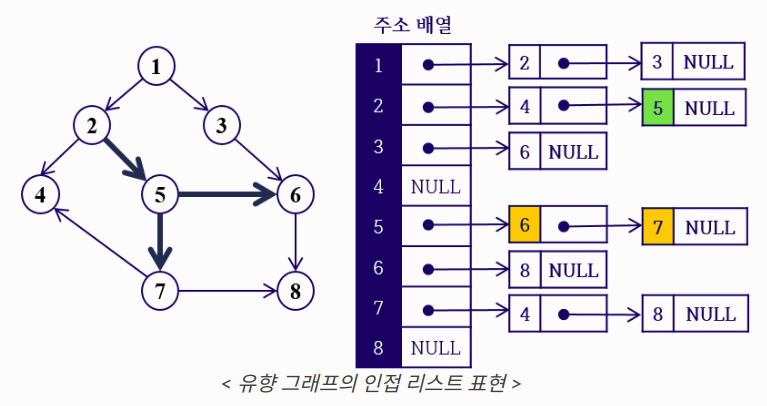
- 정점의 개수가 V개, 간선의 개수가 E개인 그래프에 대해서 V개의 연결 리스트로 그래프 정보를 저장
- 일반적으로 List(or Vector)의 배열로 구현
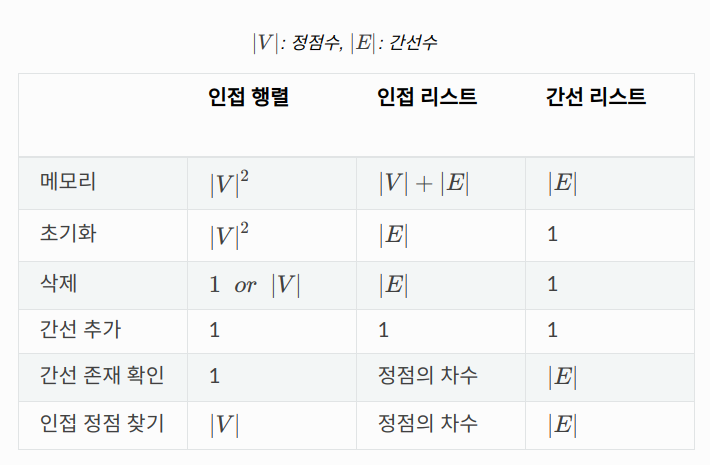
그래프 표현 방식 비교 
