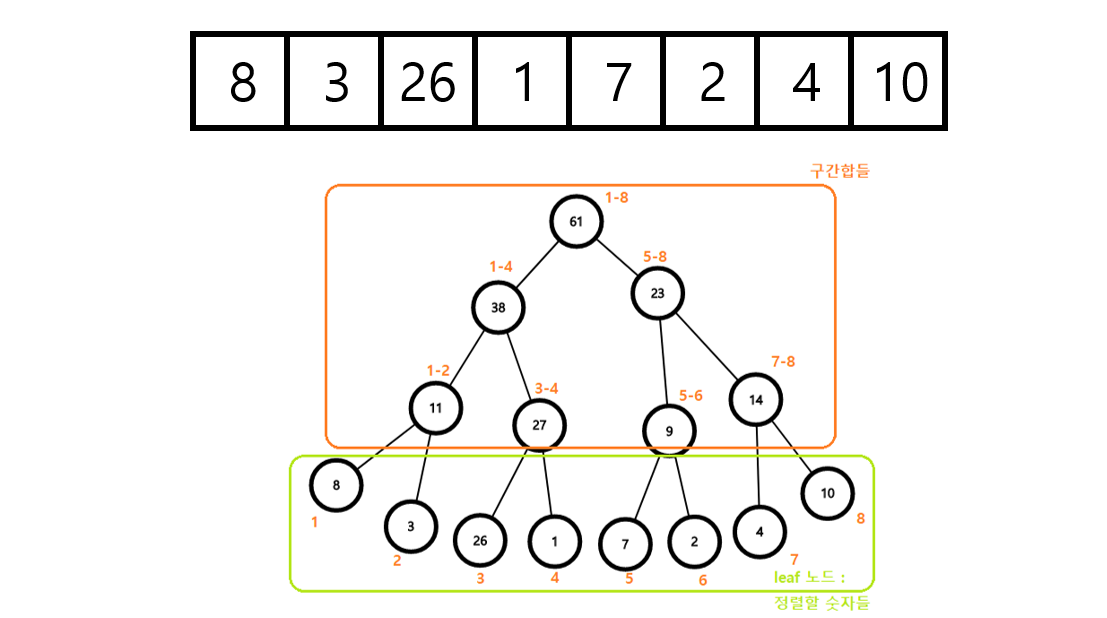
포화 이진트리(Perfect Binary Tree) 형태로, 구간의 대표값이나 연산 결과를 빠르게 얻을 수 있는 자료구조
| 방법 | 1 부분합 계속해서 구하기 | 2 특정 인덱스의 변화 | 1 + 2 |
|---|---|---|---|
| M번 실행 | O(N) | O(1) | O(NM) |
| 누적합 | O(1) | O(N) | O(NM) |
| 인덱스 트리 | O(logN) | O(logN) | O(MlogN) |
=> 부분합을 계속해서 구할 때, 특정 인덱스의 변경이 계속해서 일어날 때 유용
- 리프노드: 배열에 적혀있는 수
- 내부노드: 왼쪽 자식과 오른쪽 자식의 합
- 리프 노드의 개수가 N개 이상이 포화 이진 트리는 높이가 최소 logN
트리 구성
1. 리프 노드의 개수가 N개 이상이 되어 비어있는 공간이 발생하지 않도록 높이가 T인 트리 배연 만듦(배열크기: 2T)
2. 리프 노드(2T-1 ~ 2T-1+N-1)에 데이터 입력
3. 내부 노드(2T-1-1 ~ 1)에 양쪽 자식의 합을 입력
=> 수행시간O(N)쿼리 수행
사진은 3~5 인덱스의 합을 구하는 상황
1. 루트 노드에서 시작해서 트리를 전위 순회
2. 현재 노드가 구하고자 하는 구간에 완전히 속해있으면 그 노드의 결과값 반환
3. 왼쪽 자식에서 반환된 값과 오른쪽 자식에서 반환된 값을 더해서 반환
=> 수행시간O(logN): 루트노드~리프노드 탐색데이터 갱신
1. 해당 노드 위치의 값 수정
2. 부모를 따라 올라가면서 결과값 수정
=> 수행시간O(logN): 루트노드~리프노드
