풀이

먼저 어떤 자료구조들을 활용해 다익스트라 알고리즘을 구현할 지 생각해봤다.

• 간선의 가중치(w)까지 기록한 그래프
• 노드별 가중치 기록
• 방문 예정인 노드를 기록할 리스트 (최소 힙)

이때 방문 예정인 노드에 대한 리스트의 첫번째 원소를 pop하여 update할 다음 노드를 선택할 것인데, 다익스트라에서는 이웃 노드 중 가중치가 작은 노드부터 방문하므로 최소 힙을 활용한다.

노드 별로 출발 노드에서 i번째 노드까지의 최단 경로를 파악하려면 이전 노드가 어떤노드인지 기록해줄 필요가 있지만, 문제에서는 노드별 업데이트된 경로값(가중치 값)을 출력하면 되므로 추가하지 않았다.

그래프 구조로 저장할 때 주의할 것은 문제의 다음 사항을 신경써야 한다.

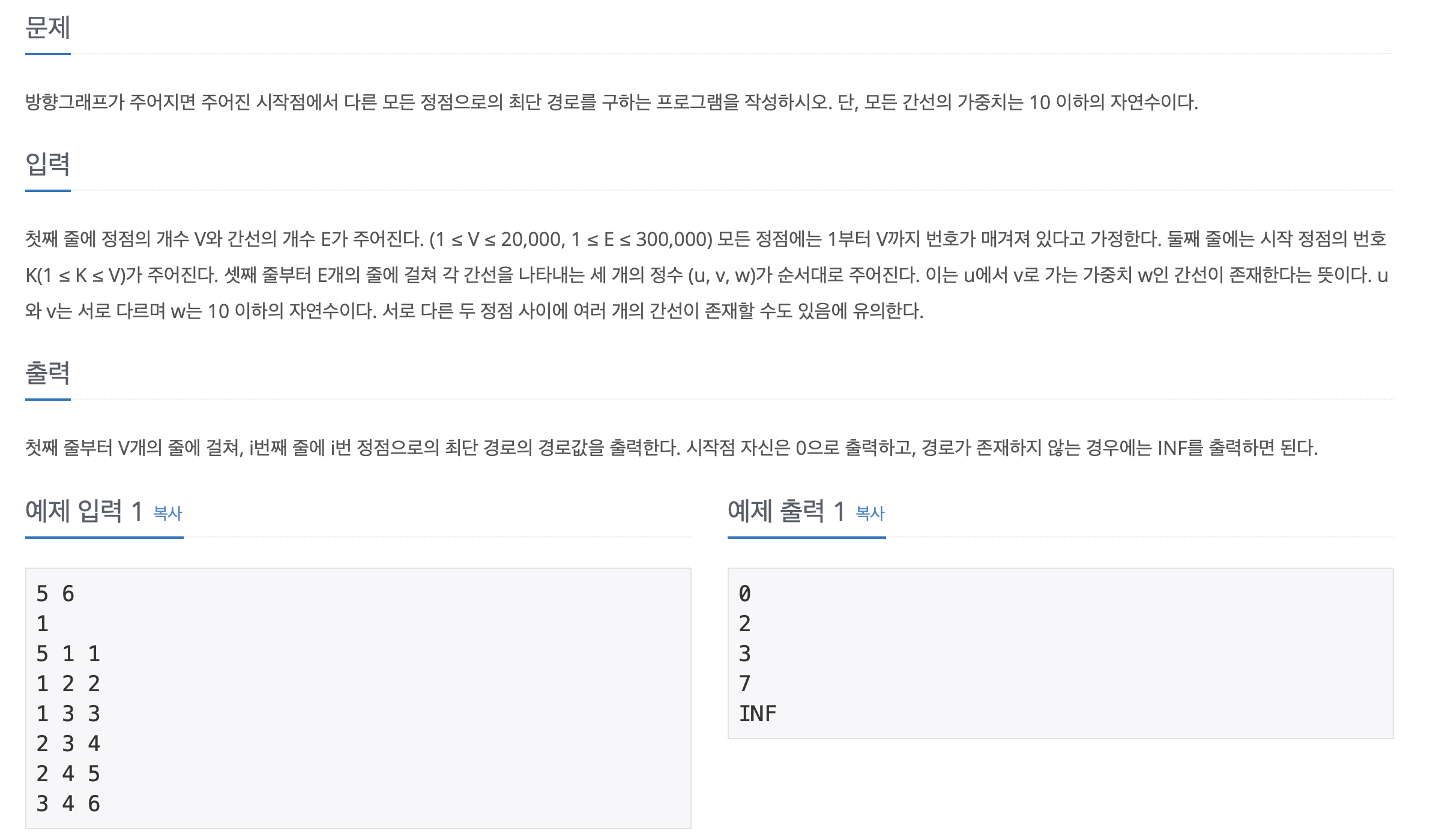
서로 다른 두 정점 사이에 여러 개의 간선이 존재할 수도 있음에 유의한다.

따라서 아래처럼 더 작은 가중치로 저장하도록 하였다.

input

u : { v1 : w1 , v2 : w2 } 형태의 이중 딕셔너리 형태로 구현해보았다.

## input
import sys
from collections import defaultdict

input = sys.stdin.readline
V, E = map(int, input().split())
start = int(input())
graph = defaultdict(dict)

for _ in range(E):
    u, v, w = map(int, input().split())
    ## 서로 다른 두 정점 사이에 여러 간선이 존재할 수 있음
    if v in graph[u].keys(): 
        graph[u][v] = min(graph[u][v], w)
    else:
        graph[u][v] = w # {1(u): {5(v) : 3(w)}}

method & output

출발 노드(s)를 제외한 모든 노드의 가중치를 ∞로 초기화 하고, 인접노드부터 차례대로 가중치를 업데이트 ( updated_w ) 한다.
이후 노드별 최단경로 가중치를 출력한다.

인접노드 중 업데이트가 필요한 노드( 현재 노드 가중치와 간선노드의 합이 인접노드(v)의 가중치보다 작은 경우 )만 방문한다.

이 때 가중치가 작은 노드부터 방문해야하므로 위에서 언급한 것과 같이 최소힙을 활용한다.

 def sol(V,E,s):
    import heapq

    # prev = dict()
    updated_w = dict()
    will_visit = [] # min heap

    # w initialization
    for v in range(1,V+1):
        if s == v:
            updated_w[v] = 0
        else:
            updated_w[v] = float('INF')
    
    # start node setting
    heapq.heappush(will_visit, (updated_w[s], s))
    
    # update shortest path
    while will_visit:
        visit_w, visit_u = heapq.heappop(will_visit)

        for adj_v, adj_w in graph[visit_u].items():
            if updated_w[adj_v] > adj_w + visit_w:
                updated_w[adj_v] = adj_w + visit_w # 가중치 업뎃
                # prev[adj_v] = visit_u # 이전경로 기록
                heapq.heappush(will_visit, (updated_w[adj_v],adj_v))

    # output of node's weight 
    for v in range(1,V+1):
        if updated_w[v] == float('inf'):
            print('INF')
        else :
            print(updated_w[v])                
            
    return
    
## output
sol(V,E,start)