
N*N 체스 판에 N개의 퀸을 놓는 상황입니다.
Example
퀸은 위, 아래, 대각선 상으로 움직일 수 있는 특성이 있습니다.
아래 예시로 N=4일 때 경우의 수를 찾는 상황입니다.
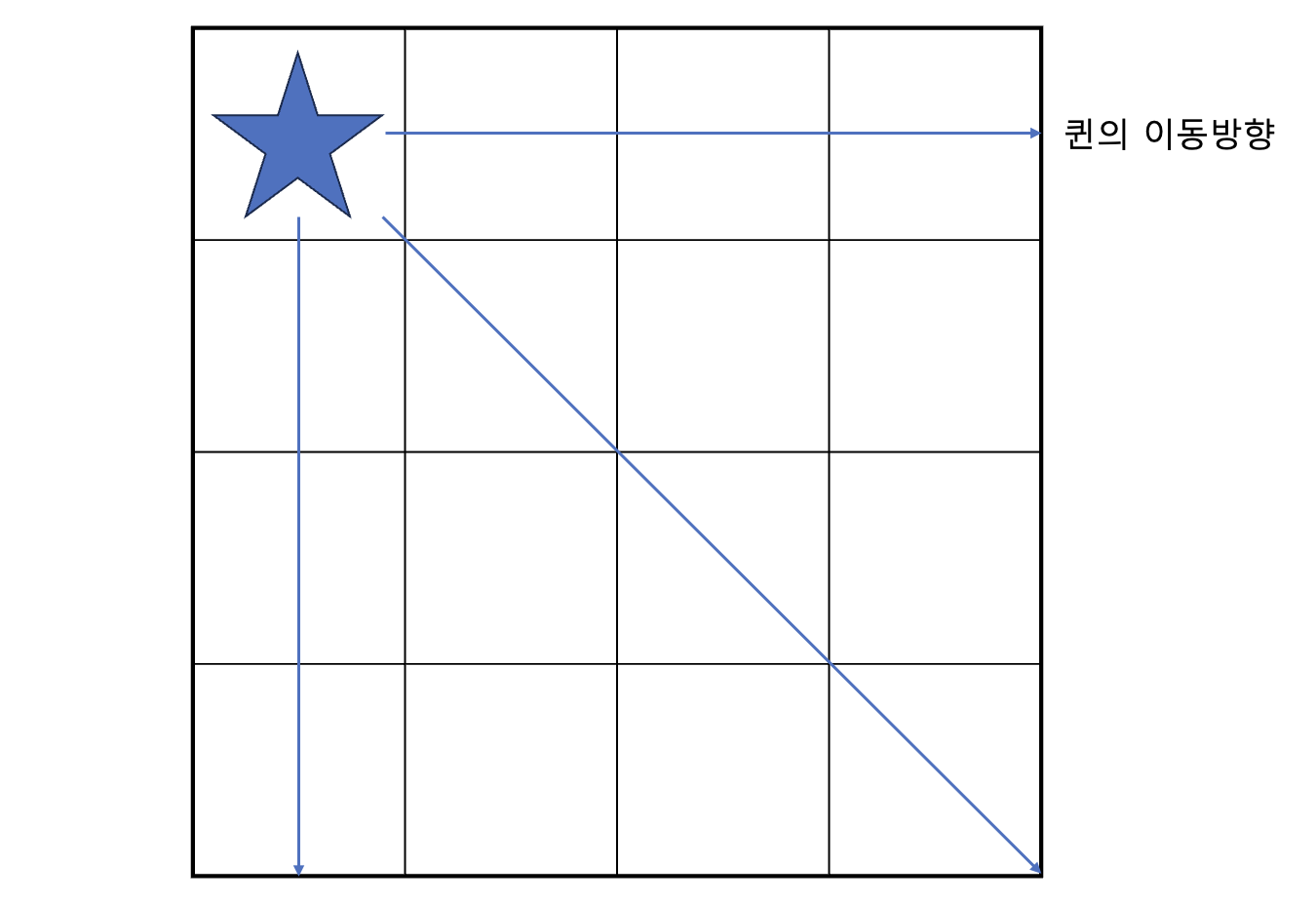
그렇다면 N개의 퀸을 모두 두려면 우선 각 행마다 하나씩의 퀸을 둔다고 생각할 수 있습니다. 같은 행에 2개 이상의 퀸이 올 수 없기 때문입니다.
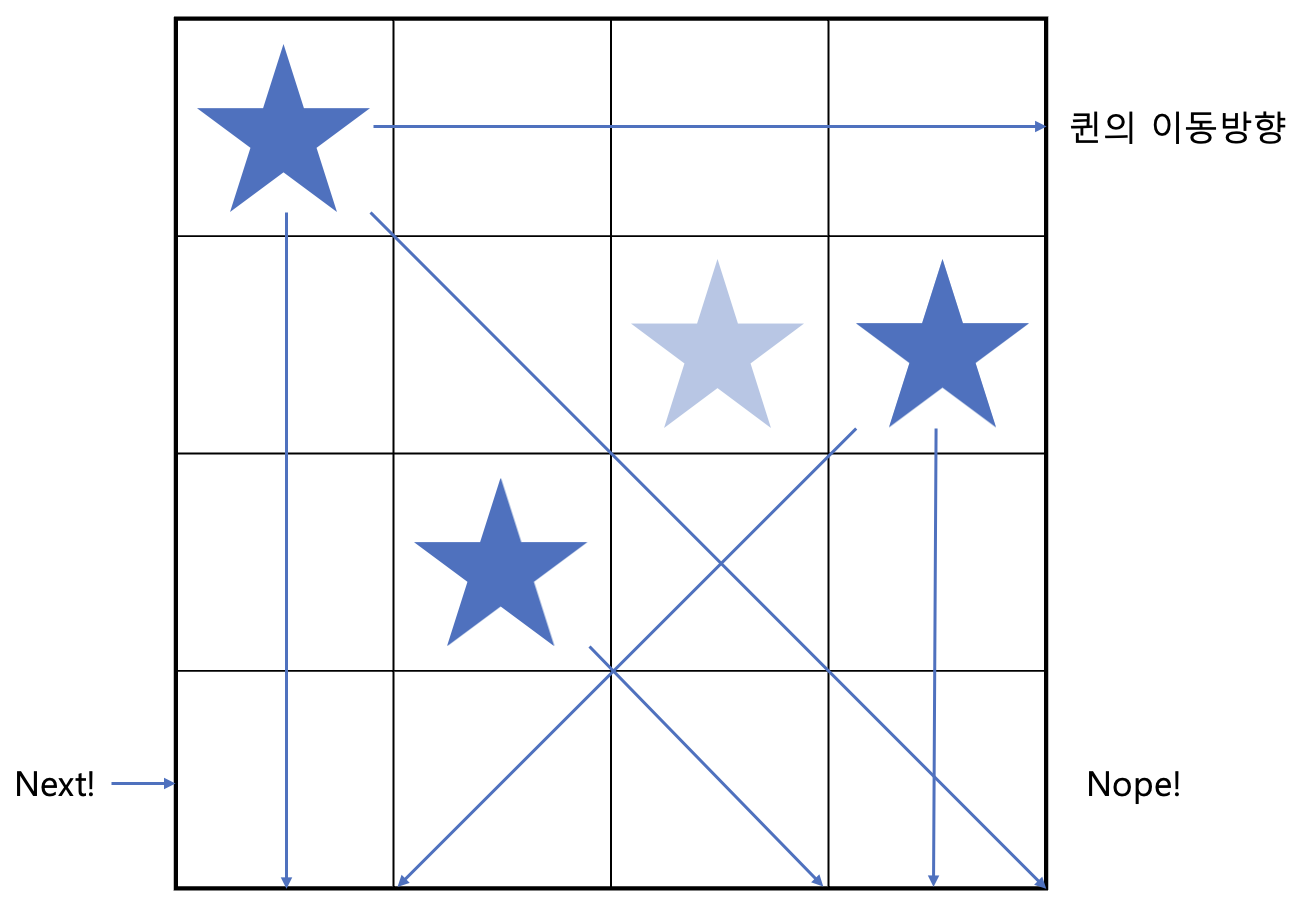
위 그림처럼 첫번째 행에 오는 퀸의 위치를 지정했다고 하면, 다음 퀸을 놓을 자리는 아래 그림처럼 찾게 됩니다.
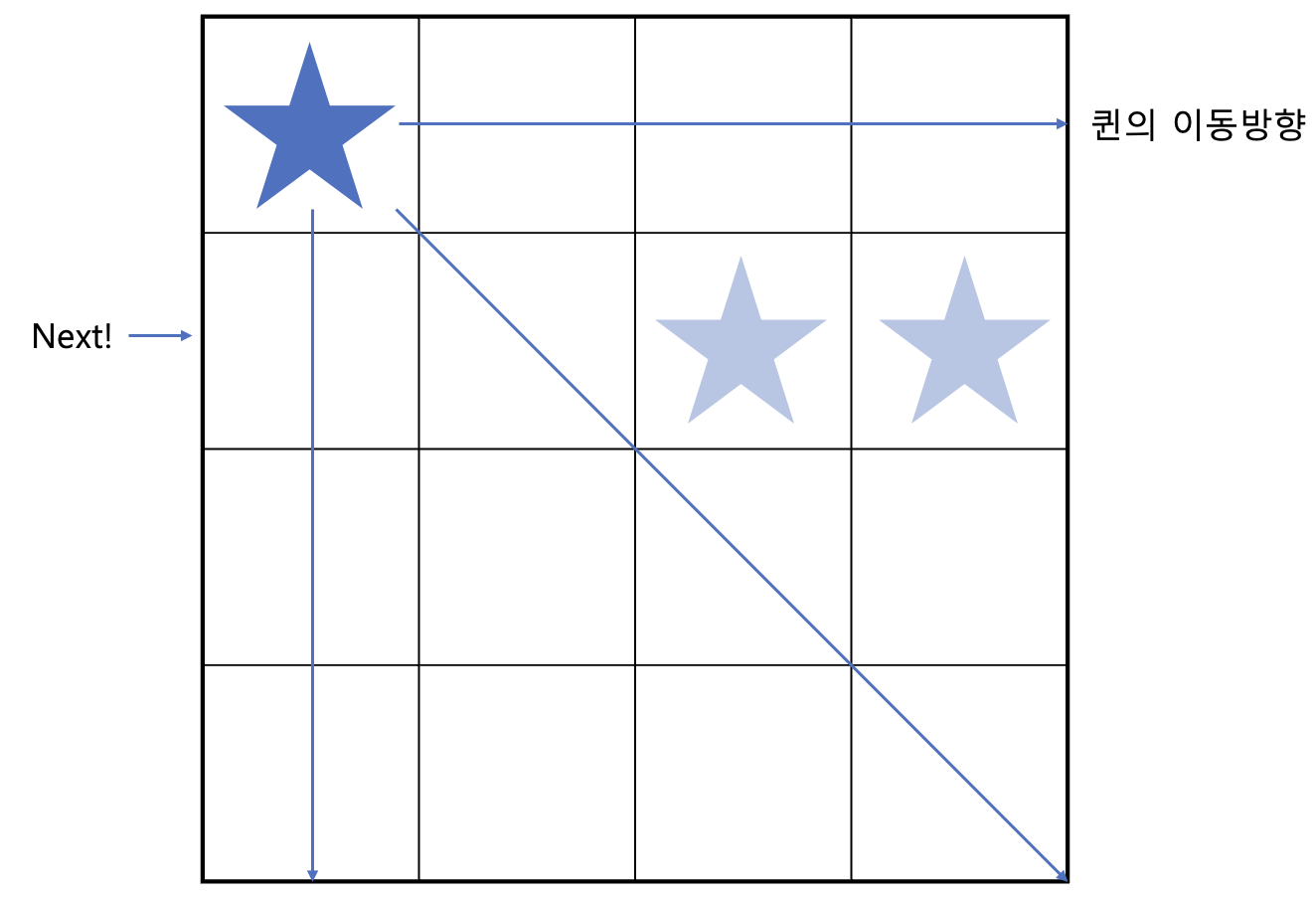
처음 퀸의 이동할 수 있는 방향인 보라색 선이 지나는 칸은 고를 수 없게됩니다.
먼저는 두번째 행에서 가능한 위치 중, 첫번째 위치를 골랐다 가정하면 아래와 같은 상황이네요. 이동 노선 표시가 너무 많아지면 난잡해질까봐 몇몇은 생략했습니다.
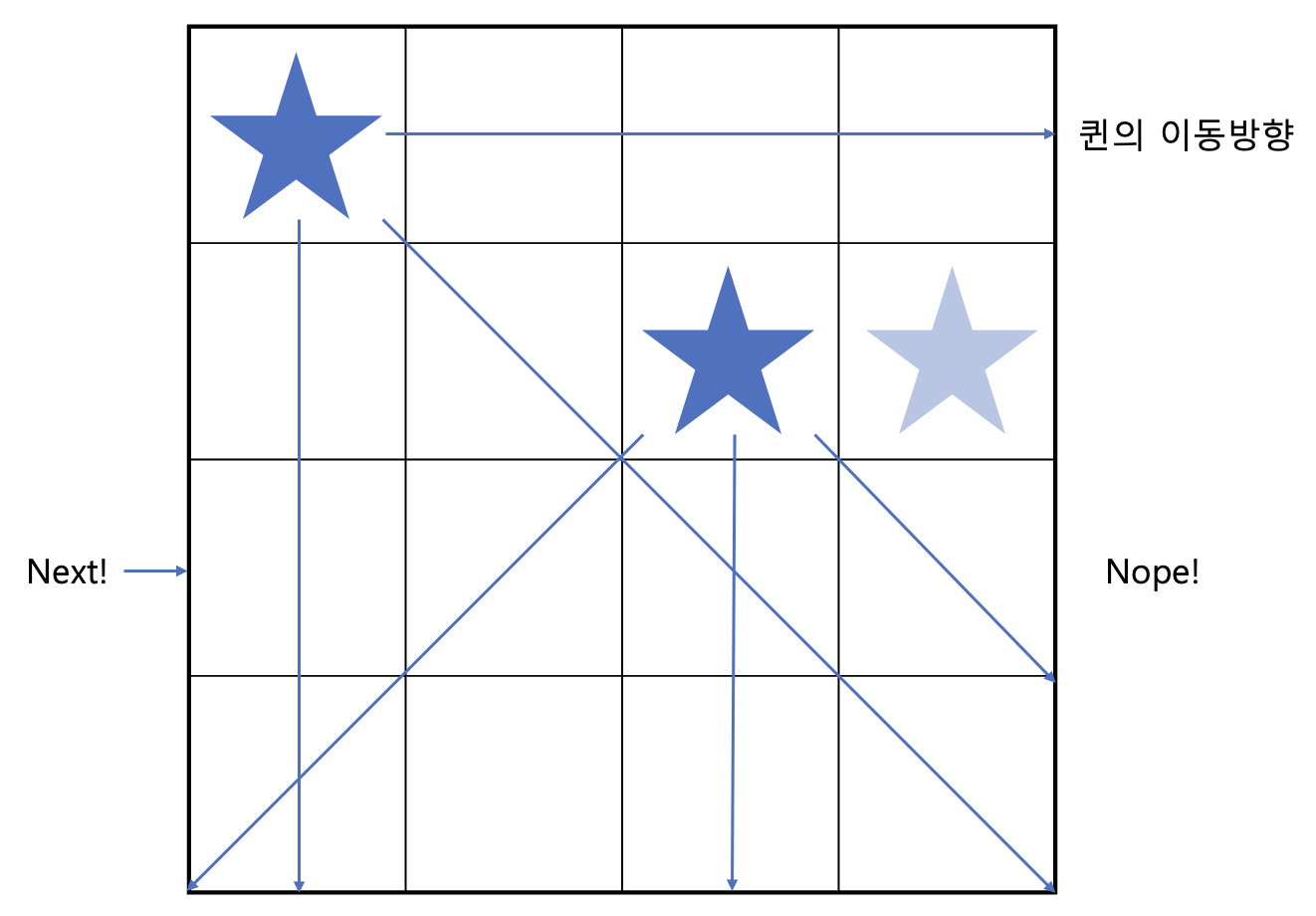
이런! 다음 행에 올 위치를 고를 때 갈 수 있는 위치가 없네요.
총 N개의 퀸을 두어야하는데 지금의 경우 N-2개 밖에 두지 못하고 막혀벼렸으니 다시 이전의 경우로 돌아가야 합니다.
가다가 막혔으니 이번엔 두번째 위치를 골랐다 가정하고 그 다음 행으로 이동해 고르는 경우도 살펴보겠습니다.
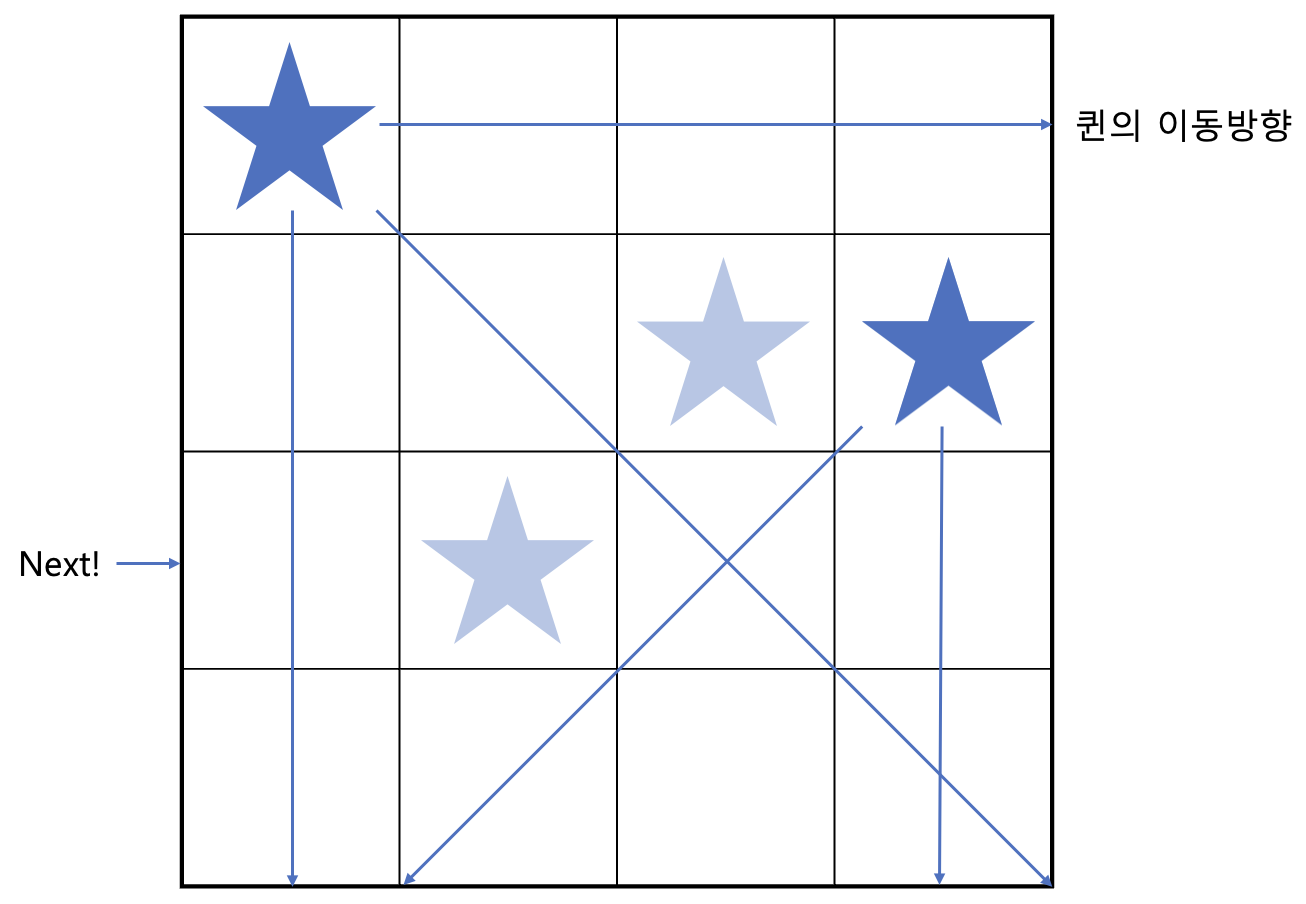
놓을 수 있는 위치가 생겼네요! 두번째 위치에 놓고 다음 행으로 넘어가 보겠습니다.
마지막에 다다랐지만,, 마지막 행에서 놓을 수 있는 위치가 없습니다 ㅠ
즉 N개의 퀸을 놓아야하지만, N-1개 밖에 놓지 못했으니, 다시 돌아가야하겟습니다.
첫번째 행의 퀸이 2번째 열을 골랐을 때부터로 돌아가야겠네요. 이후 과정은 생략하도록 하겠습니다.
만일 위처럼 행에 하나씩 퀸을 놓으면서 마지막 행까지 모두 왔다면 N개의 퀸을 둔 경우가 되므로 경우의 수에 포함되겠네요.
다시말해, 말 놓는 개수를 하나씩 늘려가며 재귀 함수를 호출하다가 이 호출 횟수가 N과 같으면 count up을 할 수 있을 것입니다.
두번째 행에서처럼, 조건을 만족하지 않으면 이전으로 돌아가 다른 경우를 탐색해보는 방식인 백 트래킹(Back-Tracking) 방식을 활용할 수 있는 문제가 되겠습니다.
조건 설정
문제 상황을 구성하려면 퀸이 지나는 위치를 어떻게 구현할지가 중요했습니다.
즉 used를 통해 해당 위치를 다른 말이 지날 수 있는 위치인지 없는 위치인지 표기할 필요가 있고, 이 조건을 참고하며 탐색을 하는 것입니다.
이를 위해 바킹독님의 백트래킹 강의에서 대각선 위치의 점유 현황 표기 방식에 대한 아이디어를 참고하였습니다.
상하좌우
우선 퀸을 하나 놓게 되면 x,y값이 같은 위치에는 놓을 수 없게 됩니다.
일단 문제를 풀 때 각 행마다 하나씩의 말을 놔보기로 했으니, 열(column)만 신경써서 퀸을 각기 다른 열에 놓을겁니다. 따라서 상하좌우에서의 위치 상태는 열 기준으로 표기를 합니다.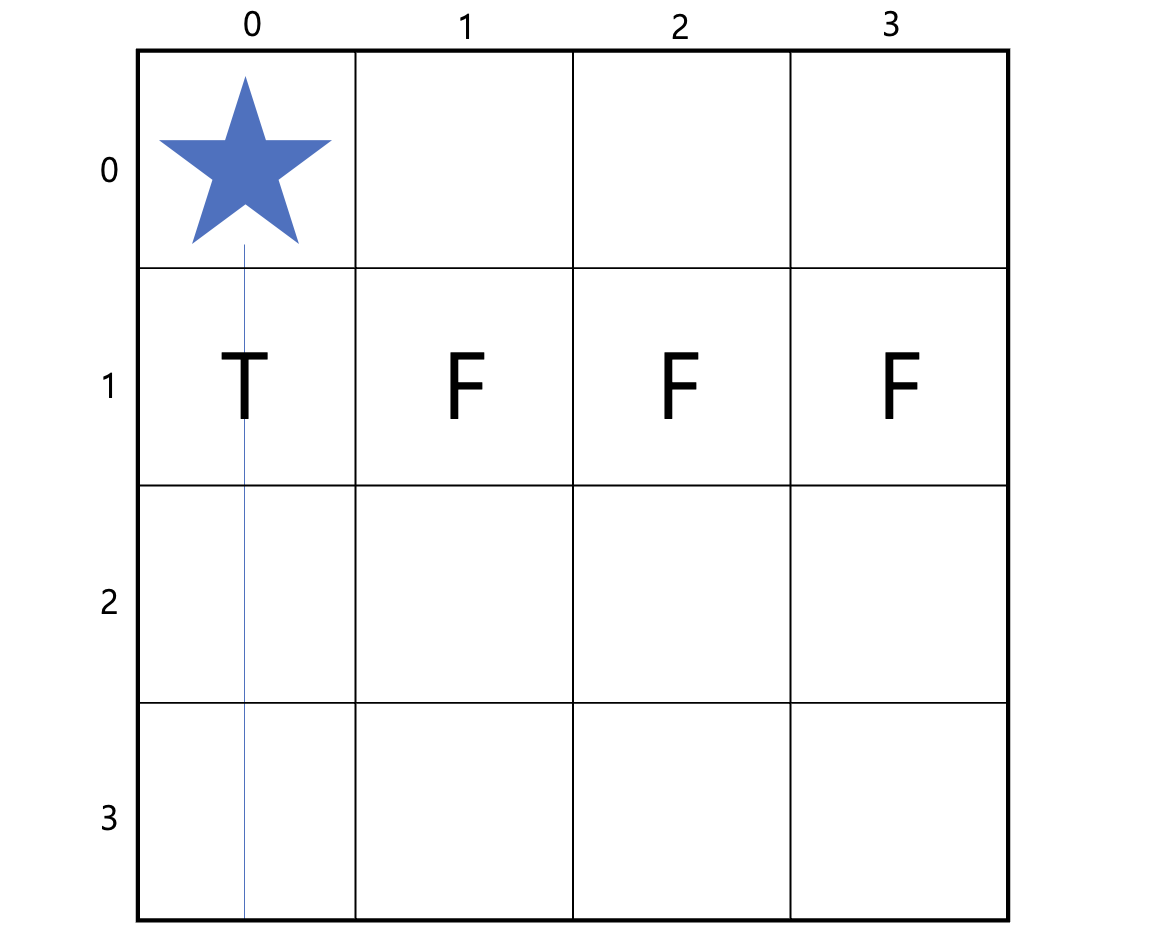
위 그림처럼 퀸을 놓고 다음 행에서 말을 놓을 때, 해당 조건식을 참고해 말을 놓게 될 것입니다.
이제 문제는 대각선 위치에 대한 조건을 만드는 건데 고민이 많이 되었고, 그만큼 좋은 방법을 배우게 됬었습니다.
대각선
y = x 방향의 대각선
해당 대각선들 위에 존재하는 좌표들은 어떤 특성을 가지고 있을까요?
행과 열번호를 ( r,c )처럼 표시한다고 하면, 임의의 좌표 ( a,b )와 같은 선상에 위치한 좌표는 아래와 같을겁니다.
- ( a, b ) , ( a - i, b + i )
a + b = ( a - i ) + ( b + i )
각각의 좌표의 공통점을 찾아보니 각 좌표에서 두 r,c 좌표끼리 더한 값은 같다는 것입니다.
즉 y = x 방향의 같은 대각선에 존재하는 좌표들은 r+c값이 같습니다.
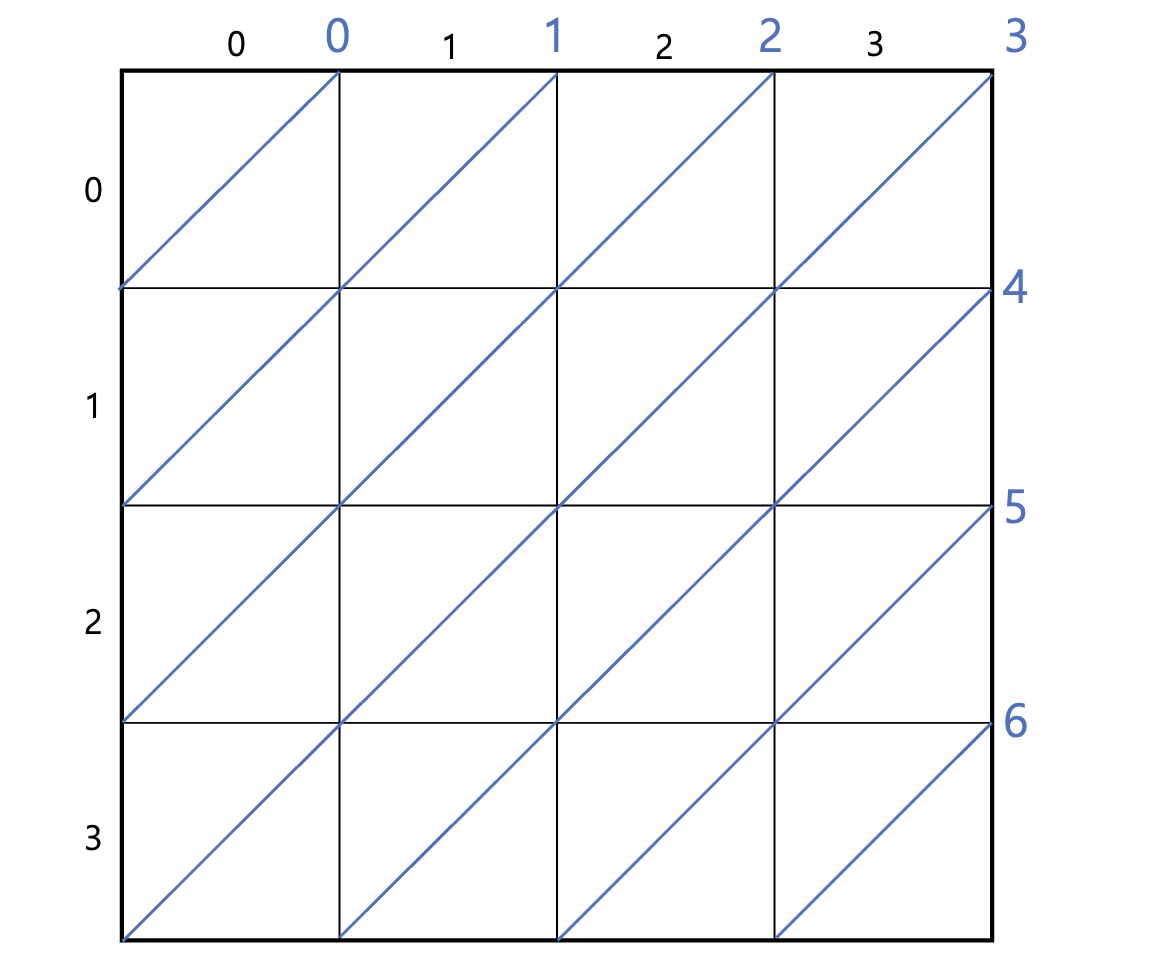
각 대각선을 지나는 좌표들의 특성을 확인해볼 수 있을거 같습니다. 0~6까지(N=4)의 크기로 해당 위치가 대각선 상 점유된 위치인지 선형적으로 표현할 수 있게 됩니다.
만일 ( 0,1 )위치에 퀸이 놓아지면 1번 index를 True로 바꿈으로써 점유상태를 표시할 수 있겠습니다. ( 1,0 ) 위치를 방문했을 때 이 위치가 점유되어 있음을 알 수 있으므로 다음으로 넘어갈 수 있게 되겠죠.
y = -x 방향의 대각선
이런 모양의 대각선들 위에 존재하는 좌표들은 어떤 특성을 가지고 있을까요?
마찬가지로 ( r,c )형태로 표기해보면, 임의의 좌표 ( a,b )와 같은 선상에 위치한 좌표는 아래와 같을겁니다.
- ( a, b ) , ( a + i, b + i )
a - b = ( a + i ) - ( b + i )
즉 y = -x 방향의 같은 대각선에 존재하는 좌표들은 r-c값이 같습니다.
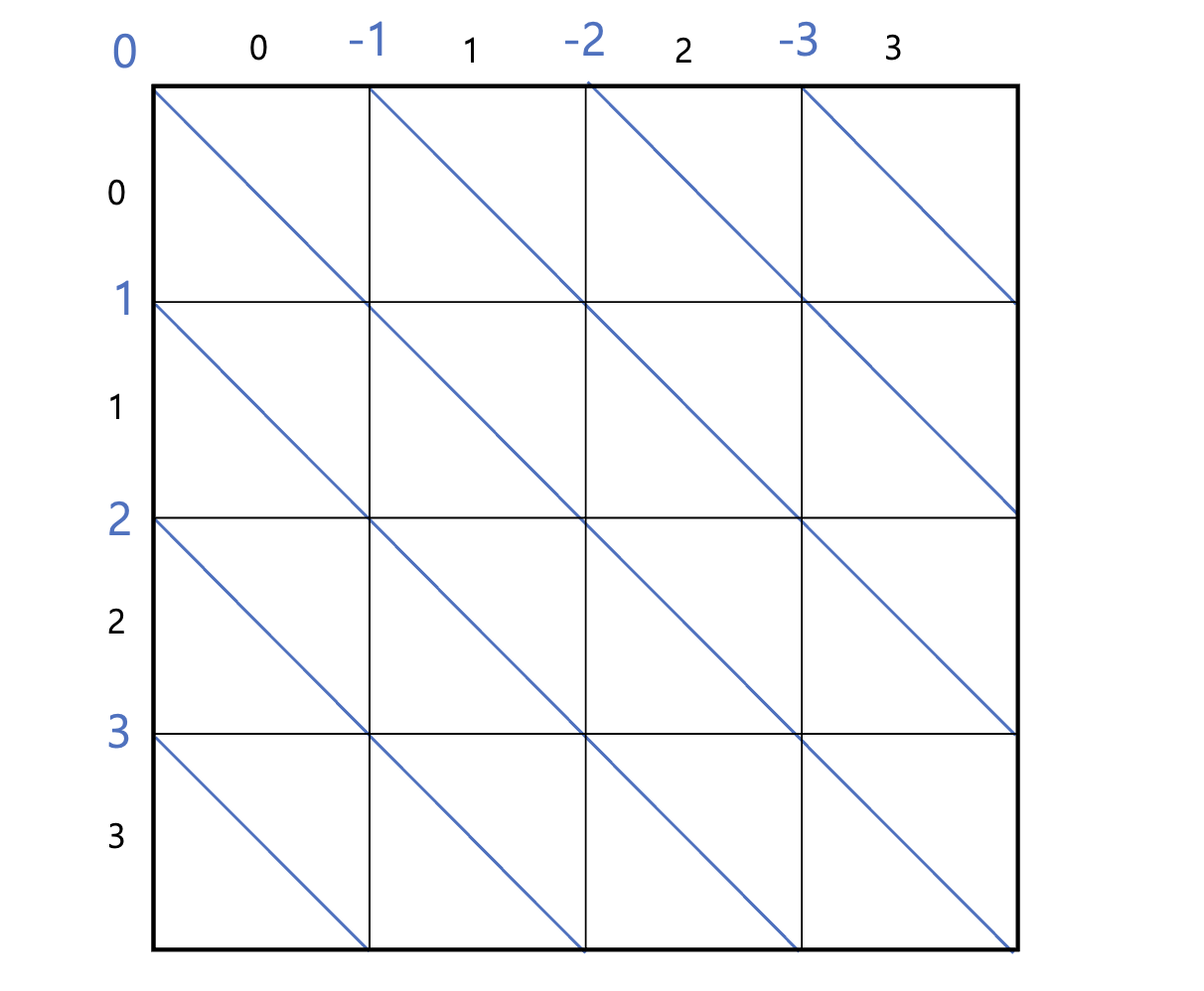
이렇게 생각하면 -3~3 ( N=4 ) 까지 값들이 나옵니다.
근데 이걸 생각해본 목적은 해당 좌표가 대각선 상에서 점유되어 있는지 선형화해서 표기하기 위함이었으니, 마이너스 범위를 메꾸기 위해 3( N-1 ) 을 더해 생각해봅시다. 만일 ( 1,2 )위치의 점유상태를 확인해보려면, used[ (n-1) + r - c ]를 참고하면 확인할 수 있겠습니다.
sol
이를 재귀형식으로 구현하면, 앞서 말했듯 호출 횟수가 퀸을 놓으려는 행 번호로 활용할 수 있고 동시에 몇개의 퀸을 놓았는지도 알 수 있게됩니다.
조건 설정에서 생각해봤던 것처럼 열방향과, y=x방향과, y=-x방향의 점유상태를 확인하면 해당 지점에 퀸을 놓을 수 있는지 판단할 수 있을 것입니다. 즉 used list 세개가 필요하고, 이를 활용해 구현할 수 있었습니다.
## method
def sol(k): # k : 놓은 말 개수 - 점유 행 번호로도 활용 가능
# 퀸 : 상하좌우 - x, y 좌표 확인 / 대각선 - (y=x 선상 : used_up) r+c 같으면. (y=-x 선상 : used_down) r-c같으면 놓을 수 없음.
global n, cnt
if k == n :
cnt += 1
return
# i : 점유 열 번호로 활용 가능
for i in range(n):
if not used_c[i] and not used_up[k+i] and not used_down[(n-1)+k-i]:
used_c[i] = True
used_up[k+i] = True
used_down[(n-1)+k-i] = True
sol(k+1)
used_c[i] = False
used_up[k+i] = False
used_down[(n-1)+k-i] = False
## input
n = int(input())
maps = [[0]*n for _ in range(n)]
# 열 점유 여부
used_c = [False]*n
# y = x 선상 점유 여부
used_up = [False]*(2*(n-1)+1)
# y = -x 선상 점유 여부
used_down = [False]*(2*(n-1)+1)
cnt = 0
## output
sol(0)
print(cnt)