[코테, 알고리즘] 백준 class 5 - 비트필드를 이용한 DP (계단수)

[1562] 계단 수

이 문제를 풀기 전에 일단

[10844] 쉬운 계단 수

이 문제부터 푸는게 낫다.

---

1. 쉬운 계단 수 (DP)

구해야하는 것 = 길이가 N인 계단수의 개수 => row

계단수를 이루는 수 = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 => col

dp[i][j] = i번째 자리에 숫자 j가 올 때, 만들어지는 계단 수의 개수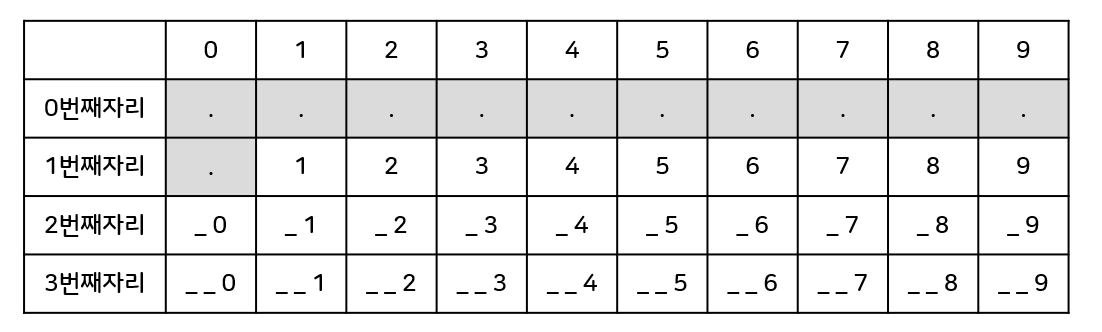

0번째자리라는 건 있을 수가 없고, 1번째 자리가 0인 경우는 계단수가 아니므로 제외한다.

이렇게 "각 칸에 써있는 꼴의 계단수의 개수"가 dp배열 안에 들어간다.

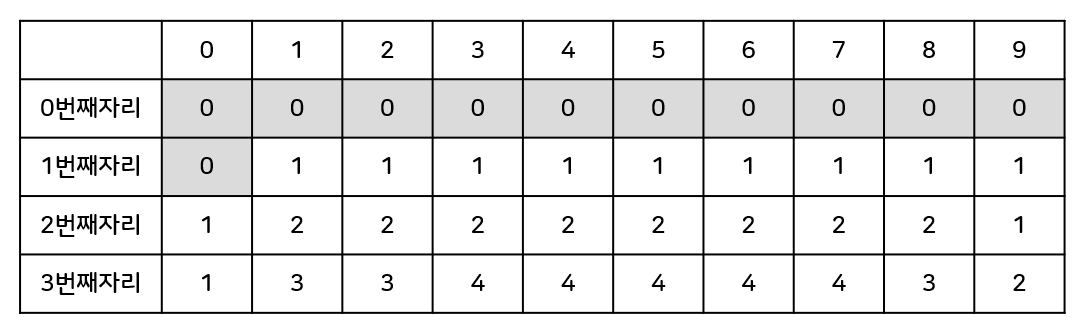
그리고, 우리는 계단수의 마지막값이 j일때(_ _ ... _ j), 계단수의 성질에 의해 그 앞에 j-1이나 j+1이 들어가야한다는 것을 알 수 있다. ex) _ _ j-1 j or _ _ j+1 j

단, 0일때는 1만, 9일때는 8만 들어갈 수 있다.

각 경우의 수는 다음과 같이 나타낼 수 있다.

코드

N = int(input())

# dp 선언 및 초기화
dp = [[0 for _ in range(10)] for _ in range(N+1)]
for i in range(1, 10):
  dp[1][i] = 1 # 계단수의 길이가 1인건(=j) 무조건 1개 (0 제외)

# dp 배열 채우기
for i in range(2, N+1): # 길이가 i인 계단수를 찾을 것이다. (길이가 2, 3, ..., N인 계단수)
  for j in range(10): # 길이가 i인 계단수의 마지막이 0,1,2,...,9일 때
    if j == 0:
      dp[i][j] = dp[i-1][1] # 계단수의 마지막이 0이려면 마지막-1이 반드시 1
    elif j == 9:
      dp[i][j] = dp[i-1][8] # 계단수의 마지막이 9이려면 마지막-1이 반드시 8
    else:
      dp[i][j] = dp[i-1][j-1] + dp[i-1][j+1] # 계단수의 마지막이 j이려면 마지막-1이 j-1이거나 j+1

# 마지막행에 있는 값들의 합이 길이가 N인 모든 계단수의 개수
print(sum(dp[N]) % 1000000000)

2. 계단 수 (DP + 비트마스킹)

비트필드를 이용한 DP

비트마스킹을 이용해서 구성한 DP 테이블을 비트필드라고 말한다.

주어진 N이 작은데 N!은 엄청 크면 이 유형이라고 한다. (어쩐지 N의 범위가 작은게 수상했음)

쉬운 계단수에서 사용한 DP를 바탕으로, 비트마스킹을 통해 0~9가 모두 사용되었는지를 표시해야한다. (2차원배열 + 비트마스킹 1차원 = 3차원배열)

dp는 다음과 같이 정의할 수 있다.

dp[길이][마지막 자리의 숫자][사용된 숫자(비트마스킹)] = 이 때의 계단수의 개수
dp[i][j][k] = 길이가 i인 수의 마지막값이 j일 때 k(비트마스킹)를 사용해서 만들 수 있는 계단수의 개수

따지려들면 엄청 복잡한데 i, j는 이전과 똑같으니 일단 무시하자.

k는 dp[i][j]를 구성하기 위해 사용한 숫자를 비트마스킹으로 나타낸 것이고(인덱스 역할), dp[i][j][k] 안에는 그렇게 해서 만든 계단수의 개수가 들어간다. (정리하자면, k를 사용해서 dp[i][j]를 만들 수 있는 계단수의 경우의 수)

k의 범위는 아무 숫자도 쓰지 않았을 때(0)부터 모든 숫자를 썼을 때(1023)이다.

# 최소 => 아무 숫자도 쓰지 않았을 때
9 8 7 6 5 4 3 2 1 0
0 0 0 0 0 0 0 0 0 0 (2) = 0(10)

# 최대 => 모든 숫자를 썼을 때
9 8 7 6 5 4 3 2 1 0
1 1 1 1 1 1 1 1 1 1 (2) = 1023(10)

ex1) 0,1,2를 사용해서 만들 수 있는 dp[i][j]를 만족하는 계단수의 수 => dp[i][j][111]
ex2) 1,3,5,7을 사용해서 만들 수 있는 dp[i][j]를 만족하는 계단수의 수 => dp[i][j][10101010]
ex3) dp[6][6][0000111110(2)]는 5,4,3,2,1을 사용해서 계단수 _ _ _ _ _ 6을 만드는 경우의 수를 의미한다.

코드를 보기 전에 핵심부터 보자.

핵심 : dp[i][j][k|1<<j] += dp[i-1][j-1][k] + dp[i-1][j+1][k]

(예시) i=6, j=6, k=0000111110 (사용한 수 : 1,2,3,4,5)

k | 1 << j
	= 0000111110 | 1 << 6
    = 0000111110 | 1000000
    = 0001111110
이제 사용한 수는 1,2,3,4,5,6이 된다.

dp[i][j][k|1<<j] = dp[6][6][0001111110] (사용한 수 : 1,2,3,4,5,6)

1,2,3,4,5,6을 사용해서 _ _ _ _ _ 6을 만드는 경우
	= 1,2,3,4,5를 사용해서 _ _ _ _ 5를 만드는 경우 + 1,2,3,4,5를 사용해서 _ _ _ _ 7을 만드는 경우

코드

N = int(input())
# dp 선언 및 초기화
dp = [[[0 for _ in range(1<<10)] for _ in range(10)] for _ in range(N+1)]
for i in range(1, 10):
  dp[1][i][1<<i] = 1 # 사용한 숫자 1개가 i밖에 없는 경우

for i in range(2, N+1): # 길이가 i인 계단수를 찾을 것이다. (길이가 2, 3, ..., N인 계단수)
  for j in range(10): # 길이가 i인 계단수의 마지막이 0,1,2,...,9일 때
    for k in range(1<<10): # 0~9를 사용할 수 있는 모든 가능한 경우의 수
      # dp[i][j][k|(1<<j)] = 사용 중인 수 k에 새로운 수 j를 추가해서 _ _ ... j(길이i)를 만드는 경우의 수 
      # dp[i-1][j-1][k] = 사용 중인 수 k로 _ _ ... j-1(길이 i-1)을 만드는 경우의 수
      # dp[i-1][j+1][k] = 사용 중인 수 k로 _ _ ... j+1(길이 i-1)을 만드는 경우의 수
      if j == 0:
        dp[i][j][k|(1<<j)] += dp[i-1][j+1][k]
      elif j == 9:
        dp[i][j][k|(1<<j)] += dp[i-1][j-1][k]
      else:
        dp[i][j][k|1<<j] += dp[i-1][j-1][k] + dp[i-1][j+1][k]
      dp[i][j][k|(1<<j)] %= 1000000000 # 문제조건에 의해 나눔

sum = 0
for i in range(10):
  sum += dp[N][i][(1<<10)-1]%1000000000 # 인덱스 오류 때문에 1<<10에서 1 빼줘야함

print(sum%1000000000)